吉林省名校调研(省命题A)2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-10 类型:期末考试
一、单选题
-
1. 某种细菌的半径约为米,数据用科学记数法表示为( )A、 B、 C、 D、2. 小东要从下面四组木棒中选择一组制作一个三角形作品,你认为他应该选( )组.A、 , , B、 , , C、 , , D、 , ,3. 下列计算正确的是( )A、 B、(-2)0=2 C、 D、4. 若分式有意义,则x的取值范围是( )A、x>2 B、x≠0 C、x≠0且x≠2 D、x≠25. 如图,直线、相交于点 , 为这两条直线外一点,连接 . 点关于直线、的对称点分别是点、 . 若 , 则点、之间的距离可能是( )
 A、 B、 C、 D、6. 如图,点在上,点在上,已知 , 添加下列一个条件后仍无法判定的是( )
A、 B、 C、 D、6. 如图,点在上,点在上,已知 , 添加下列一个条件后仍无法判定的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 当时,分式的值为 .8. 如图,在中,点、分别为边、上的点,连接 , 将沿翻折得到 , 使 . 若 , , 则的大小为 .
 9. 如图,将边长为的等边向右平移 , 得到 , 此时阴影部分的周长为 .
9. 如图,将边长为的等边向右平移 , 得到 , 此时阴影部分的周长为 . 10. 分解因式: .11. 如图, , , , 则、两点之间的距离为 .
10. 分解因式: .11. 如图, , , , 则、两点之间的距离为 . 12. 如图,在中. , , 以点为圆心,长为半径作弧,交射线于点 , 连接 . 则的度数是 .
12. 如图,在中. , , 以点为圆心,长为半径作弧,交射线于点 , 连接 . 则的度数是 . 13. 计算: .14. 当x=时, 与 互为相反数.
13. 计算: .14. 当x=时, 与 互为相反数.三、解答题
-
15. 先化简,再求值: , 其中 .16. 有若干张正方形和长方形卡片如图①所示,其中型、型卡片分别是边长为、的正方形.型卡片是长为、宽为的长方形.
 (1)、若用图①中的卡片拼成一个边长为的正方形,则需要型卡片张,型卡片张,型卡片张;(2)、将型卡片沿如图①所示虚线剪开后,拼成如图②所示的正方形,则选取型卡片张,阴影部分图形的面积可表示为;(3)、如图③,将张型卡片和张型卡片无叠合的置于长为 , 宽为的长方形中.若图②中阴影部分的面积为 , 图③中阴影部分面积为 , 记每张型、型、型卡片的面积分别为、、 , 求的值.17. 如图,在中, , 为边的中线,是边上一点(点不与点、重合),过点作于点 , 交的延长线于点 .
(1)、若用图①中的卡片拼成一个边长为的正方形,则需要型卡片张,型卡片张,型卡片张;(2)、将型卡片沿如图①所示虚线剪开后,拼成如图②所示的正方形,则选取型卡片张,阴影部分图形的面积可表示为;(3)、如图③,将张型卡片和张型卡片无叠合的置于长为 , 宽为的长方形中.若图②中阴影部分的面积为 , 图③中阴影部分面积为 , 记每张型、型、型卡片的面积分别为、、 , 求的值.17. 如图,在中, , 为边的中线,是边上一点(点不与点、重合),过点作于点 , 交的延长线于点 . (1)、求证:AD//FG;(2)、求证:;(3)、若 , 且 , 直接写出的长.18. 如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,试求出∠B的度数.
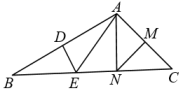
(1)、求证:AD//FG;(2)、求证:;(3)、若 , 且 , 直接写出的长.18. 如图所示,在四边形ABCD中,∠A=80°,∠C=75°,∠ADE为四边形ABCD的一个外角,且∠ADE=125°,试求出∠B的度数. 19. 如图,是等腰直角三角形, , . 动点从点出发,以每秒个单位长度的速度在射线上运动.点出发后,连接 , 以为直角边向右作等腰直角三角形 , 使 , 连接 , 设点的运动时间为秒.
19. 如图,是等腰直角三角形, , . 动点从点出发,以每秒个单位长度的速度在射线上运动.点出发后,连接 , 以为直角边向右作等腰直角三角形 , 使 , 连接 , 设点的运动时间为秒. (1)、的边上高为;(2)、求的长(用含的式子表示);(3)、就图中情形求证:≌;(4)、当::时,直接写出的值.20. 如图,在中, , 分别以、为圆心,长为半径作弧,两弧交于点 , 作射线 , 连接、 , 求的度数.
(1)、的边上高为;(2)、求的长(用含的式子表示);(3)、就图中情形求证:≌;(4)、当::时,直接写出的值.20. 如图,在中, , 分别以、为圆心,长为半径作弧,两弧交于点 , 作射线 , 连接、 , 求的度数. 21. 在平面直角坐标系中,点为坐标原点,点A(-2,2)和点B(-3,-2)的位置如图所示.
21. 在平面直角坐标系中,点为坐标原点,点A(-2,2)和点B(-3,-2)的位置如图所示. (1)、作出线段关于轴对称的线段 , 并写出点、的对称点、的坐标;(2)、连接和 , 请在图中画一条线段,将图中的四边形分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).22. 长春市政府计划对城区某道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的倍,甲队改造米的道路比乙队改造同样长的道路少用天.(1)、求乙工程队每天能改造道路的长度;(2)、若甲队工作一天的改造费用为万元,乙队工作一天的改造费用为万元,如需改造的道路全长为米,如果安排甲、乙两个工程队同时开工,并一起完成这项城区道路改造,求改造该段道路所需的总费用.
(1)、作出线段关于轴对称的线段 , 并写出点、的对称点、的坐标;(2)、连接和 , 请在图中画一条线段,将图中的四边形分成两个图形,其中一个是轴对称图形,另一个是中心对称图形,并且线段的一个端点为四边形的顶点,另一个端点在四边形一边的格点上.(每个小正方形的顶点均为格点).22. 长春市政府计划对城区某道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的倍,甲队改造米的道路比乙队改造同样长的道路少用天.(1)、求乙工程队每天能改造道路的长度;(2)、若甲队工作一天的改造费用为万元,乙队工作一天的改造费用为万元,如需改造的道路全长为米,如果安排甲、乙两个工程队同时开工,并一起完成这项城区道路改造,求改造该段道路所需的总费用.