吉林省吉林市永吉县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 等腰三角形一边长为4，一边长9，它的周长是（）

A、17 B、22 C、17或22 D、不确定

查看试题解析
2. 我们知道，一些较大的数适合用科学记数法表示，小于1的正数也可以用科学记数法表示．则0.000 025 7用科学记数法表示为（）

A、 $2.57 \times 1 0^{5}$ B、 $25.7 \times 1 0^{- 4}$ C、 $2.57 \times 1 0^{- 5}$ D、 $2.57 \times 1 0^{- 6}$ .

查看试题解析
3. 下列大学的校徽图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $(- a^{2})^{3} = a^{6}$ C、 $(3 a b^{2})^{2} = 9 a^{2} b^{4}$ D、 $4^{- 2} = \frac{1}{2}$

查看试题解析
5. 下列约分正确的是（）

A、 $\frac{a^{2} - b^{2}}{a - b} = a + b$ B、 $\frac{a - b}{b - a} = 1$ C、 $\frac{2 a + 4 b}{2} = a + 4 b$ D、 $\frac{a^{2}}{a^{2} b^{2}} = \frac{1}{b}$

查看试题解析
6. 如图，已知∠BAC=∠ABD=90°，AD和BC相交于O．在①AC=BD；②BC=AD；③∠C=∠D；④OA=OB．条件中任选一个，可使△ABC ≌△BAD．可选的条件个数为（）

A、1 B、2 C、3. D、4

查看试题解析

二、填空题

7. 正五边形每个内角的度数是.

查看试题解析
8. 因式分解： $a m^{2} - 2 a m n + a n^{2}$ = ．

查看试题解析
9. 若分式 $\frac{2 x - 4}{3 x + 6}$ 有意义，则字母x应满足的条件为．

查看试题解析
10. 如图，在△ABC中，BC=8 cm，分别以点A和点B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于两点；过这两点作直线交AC于点E，交AB于点D，若△BCE的周长为18 cm，则AC的长为cm．

查看试题解析
11. 如图，在△ABC中，∠A=90°，∠B=40°．点D和点E分别在AC和BC的延长线上，并且CD=CE，连接DE．则∠D的度数为．

查看试题解析
12. 若 $(x + 2) (x - 3) = x^{2} + b x + c$ ，其中b，c为常数，则点P（b，c）关于x轴的对称点的坐标为．

查看试题解析
13. a，b是两个实数，若 $a + b = - 3$ ， $a b = - 10$ ，则 $a^{2} + b^{2}$ 的值为．

查看试题解析
14. 如图，等边三角形ABC的边长为4 cm，点D，E分别在边AB，AC上，将△ABC沿DE折叠，使点A落在△ABC的外部F处．则整个阴影部分图形的周长为cm．

查看试题解析

三、解答题

15. 计算： $(12 a^{3} - 6 a^{2} + 3 a) \div 3 a + (- 2 a) (2 a + 1)$ ．

查看试题解析
16. 计算： $(a + 1)^{2} + (3 - a) (3 + a)$ ．

查看试题解析
17. 斑马线前“车让人”，不仅体现着对生命的尊重，也直接反映着城市的文明程度．如图，某路口的斑马线路段A－B－C横穿双向行驶车道，其中AB=BC=12米，在绿灯亮时，晓雯共用9秒通过AC，其中通过BC段的速度是通过AB段速度的2倍，求晓雯通过AB段时的速度．

查看试题解析
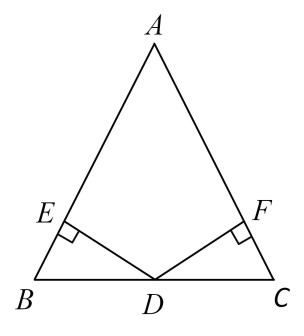
18. 如图，在△ABC中，AB=AC，点D在BC上，且BD=CD，DE⊥AB于E，DF⊥AC于F．
求证：△BDE ≌△CDF．

查看试题解析
19. 先化简，再求值： $(\frac{x^{2}}{x - 1} + \frac{9}{1 - x}) \div \frac{x^{2} + 3 x}{x - 1}$ ， x在1，2，－3中选取合适的数．

查看试题解析
20. 如图，点D，E在△ABC的边BC上，AB=AC，AD=AE．

(1)、图中有个三角形（包括△ABC），有对全等三角形．

(2)、求证：BD=CE．

查看试题解析
21. 如图①，图②，图③都是4×4的正方形网格，每个小正方形的顶点称为格点．A，B两点均在格点上，在给定的网格中，按下列要求画图：

（ 1 ）在图①中，画出以AB为底边的等腰△ABC，并且点C为格点．

（ 2 ）在图②中，画出以AB为腰的等腰△ABD，并且点D为格点．

（ 3 ）在图③中，画出以AB为腰的等腰△ABE，并且点E为格点，所画的△ABE与图②中所画的△ABD不全等．

查看试题解析
22. 如图，△ABC是等边三角形，点E在AC边上，连接BE，以BE为一边作等边△BED，连接AD.

(1)、求证：CE=AD．

(2)、若BC=8 cm，BE=7 cm，则△ADE的周长为cm．

查看试题解析
23. 如图，在△ABC中，AB＝AC，D为BC边上一点，∠B＝30°，∠DAB＝45°.

(1)、求∠DAC的度数；

(2)、求证：DC＝AB.

查看试题解析
24. 阅读下列材料：
一般地，没有公因式的多项式，当项数为四项或四项以上时，经常把这些项分成若干组，然后各组运用提取公因式法或公式法分别进行分解，之后各组之间再运用提取公因式法或公式法进行分解，这种因式分解的方法叫做分组分解法．如：
因式分解： $a m + b m + a n + b n$
＝ $(a m + b m) + (a n + b n)$
＝ $m (a + b) + n (a + b)$
＝ $(a + b) + (m + n)$

(1)、利用分组分解法分解因式：
① $3 m - 3 y + a m - a y$ ；
② $a^{2} x + a^{2} y + b^{2} x + b^{2} y$

(2)、因式分解： $a^{2} + 2 a b + b^{2} - 1$ =（直接写出结果）．

查看试题解析
25. 某文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．

(1)、求第一批购进书包的单价是多少元？

(2)、若商店销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？

查看试题解析
26. 如图，ED⊥AB，FC⊥AB，垂足分别为D，C，并且AC=BD，AE=BF，连接CE．

(1)、求证：AE∥FB；

(2)、若DC=DE，∠A=25°，求∠AEC的度数．

(3)、若DC=DE，∠A=α，则∠AEC=（用含α的式子表示）．

(4)、若∠A=30°，DE=m，则BF=（用含m的式子表示）．

查看试题解析