吉林省白城市通榆县2021-2022学年八年级上学期期末数学试题
试卷更新日期：2022-01-10 类型：期末考试
一、单选题
-
1. 计算a2•a的结果是（ ）A、a2 B、2a3 C、a3 D、2a22. 2017年12月15日，北京2022年冬奥会会徽“冬梦”正式发布. 以下是参选的会徽设计的一部分图形，其中是轴对称图形的是（ ）A、
B、
C、
D、
3. 一个等腰三角形的两边长分别为3 cm和7 cm，则此三角形的周长为（ ）A、13 cm B、17 cm C、7 cm或13 cm D、不确定4. 从边长为a的正方形中剪掉一个边长为b的正方形（如图1所示），然后将剩余部分拼成一个长方形（如图2所示）．根据图形的变化过程，写出的一个正确的等式是（ ）
A、（a－b）2＝a2－2ab＋b2 B、a（a－b）＝a2－ab C、b（a－b）＝ab－b2 D、a2－b2＝（a＋b）（a－b）5. 如图，已知∠1＝∠2，要说明△ABD≌△ACD，还需从下列条件中选一个，错误的选法是（ ）
A、∠ADB＝∠ADC B、∠B＝∠C C、DB＝DC D、AB＝AC6. 如图，△ABC中，AB=AC，∠B=40°．把△ABC的边AC对折，使顶点C和点A重合，折痕交BC于D，连接AD，则∠BAD的度数为（ ）
A、50° B、55° C、60° D、65°二、填空题
-
7. 分解因式：2x2－4x=.8. 一个氧原子的直径为0.000000000148m，用科学记数法表示为m.9. 若分式 的值为零，则x的值为 ．
10. 若25x2－mxy+9y2是完全平方式，则m的值为11. 如图，李叔叔家的凳子坏了，于是他给凳子加了两根木条，这样凳子就比较牢固了，他所应用的数学原理是 ．
12. 如图，△ABC中，∠C＝80°，若沿图中虚线截去∠C，则∠1+∠2＝ ．
13. 如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P= ．
14. 如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①BE=CG；②DF=DH；③BH=CF；④AF=CH．其中正确的是.
三、解答题
-
15. 下面是小颖化简整式的过程，仔细阅读后解答所提出的问题．
解：x（x＋2y）－（x＋1）2＋2x
＝（x2＋2xy）－（x2＋2x＋1）＋2x第一步
＝x2＋2xy－x2＋2x＋1＋2x第二步
＝2xy＋4x＋1第三步
(1)、小颖的化简过程从第步开始出现错误，错误的原因是 ．(2)、写出此题正确的化简过程．16. 如果一个多边形的内角和是外角和的3倍还多180°，那么这个多边形的边数是多少？17. 解方程：
18. 如图，点B，F，C，E在一条直线上，FB=CE，AB∥ED，AC∥FD。求证：AB=DE.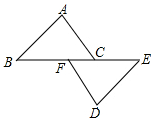
19. 如图，ΔABC中，A点坐标为(2，4)，B点坐标为(-3，-2)，C点坐标为(3，1).
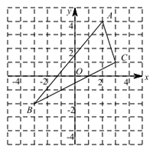(1)、在图中画出ΔABC关于y轴对称的ΔA′B′C′(不写画法)，并写出点A′，B′，C′的坐标；(2)、求ΔABC的面积.20. 今年我县在老旧小区改造方面取得了巨大成就，人居环境得到了很大改善．如图，有一块长（3a＋b）米，宽（2a＋b）米的长方形广场，园林部门要对阴影区域进行绿化，空白区域进行广场硬化，阴影部分是边长为（a＋b）米的正方形．
(1)、计算广场上需要硬化部分的面积．(2)、若a＝30，b＝10，求硬化部分的面积．21. 如图，已知∠AOB，作∠AOB的平分线OC，将直角尺DEMN如图所示摆放，使EM边与OB边重合，顶点D落在OA边上，DN边与OC交于点P． 猜想△DOP是三角形什么三角形？；并说明理由
22.(1)、（阅读理解）课外兴趣小组活动时，老师提出了如下问题：
如图1，△ABC中，若AB＝8，AC＝6，求BC边上的中线AD的取值范围.小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：
由已知和作图能得到△ADC≌△EDB的理由是____.
A、SSS B、SAS C、AAS D、HL(2)、求得AD的取值范围是____.A、6＜AD＜8 B、6≤AD≤8 C、1＜AD＜7 D、1≤AD≤7(3)、（感悟）解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
（问题解决）
如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF.求证：AC＝BF.
23. 某商店经销一种纪念品，11月份的营业额为2000元．为扩大销售，12月份该商店对这种纪念品打九折销售，结果销售量增加20件，营业额增加700元．(1)、求这种纪念品11月份的销售单价；(2)、11月份该商店销售这种商品件；(3)、若11月份销售这种纪念品获利800元，求12月份销售这种纪念品获利多少元？24. 如图，在△ABC中，AB＝BC＝AC＝12cm，点D为AB上的点，且BD＝AB，如果点P在线段BC上以3cm/s的速度由B点向终点C运动，同时，点Q在线段CA上由C点向终点A运动．当一点到达终点时，另一点也随之停止运动．
(1)、如（图一）若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由．(2)、如（图二）若点Q的运动速度与点P的运动速度相等（点P不与点B和点C重合），连接点A与点P，连接点B与点Q，并且线段AP，BQ相交于点F，求∠AFQ的度数．(3)、若点Q的运动速度为6cm/s，当点Q运动几秒后，可得到等边△CQP？