黑龙江省大庆市肇源县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-10 类型：期末考试

进入出卷网下载

一、单选题

1. 如果一个三角形是轴对称图形，且有一个内角是60°，那么这个三角形是( )

A、等边三角形 B、等腰直角三角形 C、等腰三角形 D、含30°角的直角三角形

查看试题解析
2. 若a＜b，则下列变形正确的是（）

A、a－1 $>$ b－1 B、 $\frac{a}{4} > \frac{b}{4}$ C、－3a $>$ －3b D、 $\frac{1}{a} > \frac{1}{b}$

查看试题解析
3. 将点 $P (2 m + 3 ， m - 2)$ 向上平移2个单位得到 $P$ ，且 $P$ 在 $x$ 轴上，那么点 $P$ 的坐标是（）

A、 $(3 ， - 2)$ B、 $(3 ， 0)$ C、 $(7 ， 0)$ D、 $(9 ， 1)$

查看试题解析
4. 已知分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，那么x的值为（）

A、0 B、﹣1 C、1 D、±1

查看试题解析
5. 如图，在 $Δ A B C$ 中，分别以点 $A$ 和点 $C$ 为圆心，以大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于 $M 、 N$ 两点；做直线 $M N$ 分别交 $B C 、 A C$ 于点 $D 、 E$ ．若 $A E = 6 c m$ ， $Δ A B D$ 的周长为 $26 c m$ ，则 $Δ A B C$ 的周长为（）

A、 $32 c m$ B、 $38 c m$ C、 $44 c m$ D、 $50 c m$

查看试题解析
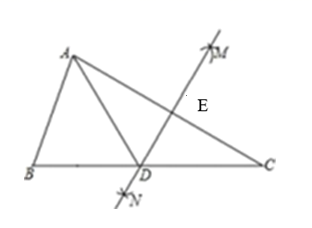6. 已知一次函数y＝kx+b的图象如图，则不等式ax+b≥2的解集为（）

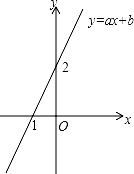A、x＜1 B、x＞1 C、x＝0 D、x≥0

查看试题解析
7. 已知x²＋kx＋4可以用完全平方公式进行因式分解，则k的值为（）

A、－4 B、2 C、4 D、±4

查看试题解析
8. 下列说法正确的是（）

A、平行四边形是轴对称图形 B、平行四边形的邻边相等 C、平行四边形的对角线互相垂直 D、平行四边形的对角线互相平分

查看试题解析
9. 若关于x的方程x＋k＝2x﹣1的解是负数，则k的取值范围是（）

A、k＞﹣1 B、k＜﹣1 C、k≥﹣1 D、k≤﹣1

查看试题解析
10. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， $A B = \frac{1}{2} B C = 1$ ，则下列结论：①∠CAD=30° ② $B D = \sqrt{7}$ ③S_{平行四边形ABCD}=AB•AC ④ $O E = \frac{1}{4} A D$ ，正确的个数是（）

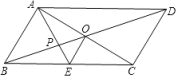A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知分式 $\frac{x - 2}{x + 3}$ 无意义，则x=。

查看试题解析
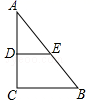
12. 分解因式： $a b^{2} - 9 a$ =.

查看试题解析
13. 在四边形ABCD中，若AB//CD，BCAD，则四边形ABCD为平行四边形．

查看试题解析
14. 一个多边形的内角和是它的外角和的两倍，则这个多边形的边数为．

查看试题解析
15. 如图，Rt△ABC中，∠C=90°，BC=6，AC=8，D、E分别为AC、AB的中点，连接DE，则△ADE的面积是．

查看试题解析
16. 某项建筑工程，由甲工程队承包需要 $a$ 天完成，由乙工程队承包需要 $b$ 天完成，则甲乙两工程队合作承包，完成工程的一半需要的天数为天

查看试题解析
17. 若不等式组 ${\begin{matrix} x > - 3 \\ x < a \end{matrix}$ 无解，则a的取值范围是．

查看试题解析
18. 如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论中正确的有（填序号）①△BPQ是等边三角形②△PCQ是直角三角形③∠APB＝150° ④∠APC＝120°

查看试题解析

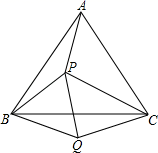
三、解答题

19. 解分式方程：

(1)、 $\frac{2}{x + 1} = \frac{3}{x}$

(2)、 $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$

查看试题解析
20. 先化简 $\frac{x^{2} - 4 x + 4}{x^{2} - 1} \div \frac{x^{2} - 2 x}{x + 1} + \frac{1}{x - 1}$ ，再从 $- 2$ ， $- 1$ ，0，1，2中选一个合适的数作为x的值代入求值.

查看试题解析
21. 解不等式组 ${\begin{array}{l} 5 x - 3 \leq 2 x + 9 \\ 3 x > \frac{x + 10}{2} \end{array}$ ，并写出它的所有整数解．

查看试题解析
22. 已知方程 $\frac{2}{1 + x} - \frac{k}{1 - x} = \frac{6}{x^{2} - 1}$ 有增根x=1，求k的值.

查看试题解析
23. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（1，3）．

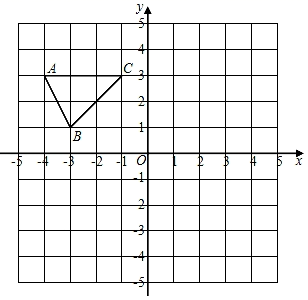(1)、请按下列要求画图：
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A₁B₁C₁ ，画出△A₁B₁C₁；
②△A₂B₂C₂与△ABC关于原点O成中心对称，画出△A₂B₂C₂ ．

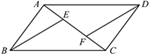
(2)、在（1）中所得的△A₁B₁C₁和△A₂B₂C₂关于点M成中心对称，请写出对称中心M点的坐标．

查看试题解析
24. 如图，在△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，求证：BE＝CF.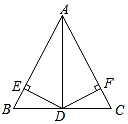

查看试题解析
25. 如图，E、F是□ABCD对角线AC上的两点，AF=CE.
求证：BE=DF．

查看试题解析
26. 如图，已知△ABC的BC边的垂直平分线DE与∠BAC的平分线交于点E，EF⊥AB的延长线于点F，EG⊥AC于点G，求证：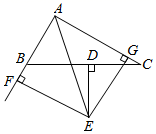

(1)、BF＝CG；

(2)、AB+AC＝2AG．

查看试题解析
27. 针对资源急需问题，某医疗设备公司紧急复工，但受疫情影响，医用防护服生产车间仍有7人不能到厂生产．为了应对疫情，已复产的工人加班生产，由原来每天工作8小时增加到10小时，每小时完成的工作量不变．原来每天能生产防护服800套，现在每天能生产防护服650套．

(1)、求原来生产防护服的工人有多少人？

(2)、复工10天后，未到的工人同时到岗加入生产，每天生产时间仍然为10小时．公司决定将复工后生产的防护服14500套捐献给某地，则至少还需要生产多少天才能完成任务？

查看试题解析
28. 如图，在△ABC中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且CF＝3BF，连接DB，EF．

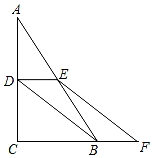(1)、求证：四边形DEFB是平行四边形；

(2)、若∠ACB＝90°，AC＝12cm，DE＝4cm，求四边形DEFB的周长．

查看试题解析