2022年高考数学二轮复习选择填空题型 17 椭圆

试卷更新日期：2022-01-10 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知点 $A ， B$ 在椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 上， $M$ 与 $A$ 关于原点对称， $∠ M A B = 9 0^{∘}$ ， $M B$ 交 $y$ 轴于点 $Q$ ， $O$ 为坐标原点， $\vec{O M} \cdot \vec{O Q} = 2 {\vec{O Q}}^{2}$ ，则椭圆的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
2. 已知 $P$ 是椭圆 $x^{2} + 5 y^{2} = 25$ 上一点， $F_{1}$ ， $F_{2}$ 为椭圆的左，右焦点，且 $| P F_{1} | = 7$ ，则 $| P F_{2} | =$ （）

A、1 B、3 C、5 D、9

查看试题解析
3. 已知抛物线 $y = \frac{1}{4} x^{2}$ 的焦点与椭圆 $\frac{y^{2}}{m} + \frac{x^{2}}{2} = 1$ 的一个焦点重合，则 $m =$ （）

A、1 B、3 C、5 D、7

查看试题解析
4. “ $0 < m < 2$ ”是“方程 $\frac{x^{2}}{m} + \frac{y^{2}}{2 - m} = 1$ 表示椭圆”的（）

A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件

查看试题解析
5. 已知椭圆过点 $P (\frac{3}{5} ， - 4)$ 和点 $Q (- \frac{4}{5} ， - 3)$ ，则此椭圆的方程是（）

A、 $\frac{y^{2}}{25} + x^{2} = 1$ B、 $\frac{x^{2}}{25} + y^{2} = 1$ 或 $x^{2} + \frac{y^{2}}{25} = 1$ C、 $\frac{x^{2}}{25} + y^{2} = 1$ D、以上均不正确

查看试题解析
6. 已知点 $A$ 是椭圆 $\frac{x^{2}}{2} + y^{2} = 1$ 的上顶点， $F_{1} ， F_{2}$ 分别是椭圆左右焦点，直线 $y = a x + b (a > 0)$ 将三角形 $A F_{1} F_{2}$ 分割为面积相等两部分，则 $b$ 的取值范围是（）

A、 $(0 ， 1)$ B、 $(1 - \frac{\sqrt{2}}{2} ， \frac{1}{2})$ C、 $(1 - \frac{\sqrt{2}}{2} ， \frac{1}{3}]$ D、 $[\frac{1}{3} ， \frac{1}{2})$

查看试题解析
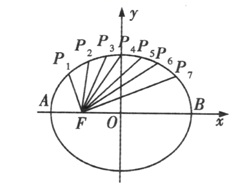7. 如图，把椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 的长轴 $A B$ 分成8等份，过每个分点作 $x$ 轴的垂线分别交椭圆的上半部分于点 $P_{1}$ ， $P_{2}$ ，…， $P_{7}$ ， $F$ 是左焦点，则 $| P_{1} F | + | P_{2} F | + \cdot \cdot \cdot + | P_{7} F | =$ （）

A、21 B、28 C、35 D、42

查看试题解析
8. 设椭圆 $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ 的左右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在椭圆上，且满足 $\vec{P F_{1}} \cdot \vec{P F_{2}} = 9$ ，则 $| P F_{1} | \cdot | P F_{2} |$ 的值为（）

A、8 B、10 C、12 D、15

查看试题解析
9. 已知椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{25} = 1$ 的一个焦点为F，双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{5} = 1$ 的左、右焦点，分别为 $F_{1}$ ， $F_{2}$ ，点P是双曲线左支上一点，则 $△ P F F_{2}$ 周长的最小值为（）

A、5 B、 $5 + \sqrt{3}$ C、10 D、14

查看试题解析
10. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{4} = 1 (a > 0)$ 与直线 $x - 4 y - 6 = 0$ 交于A，B两点，点 $M (2 ， - 1)$ 满足 $2 \vec{A M} = \vec{A B}$ ，则 $a$ 的值为（）

A、 $4 \sqrt{2}$ B、6 C、 $\sqrt{30}$ D、 $2 \sqrt{7}$

查看试题解析

二、多选题

11. 我们通常称离心率为 $\frac{\sqrt{5} - 1}{2}$ 的椭圆为“黄金椭圆”．如图，已知C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $A_{1}$ ， $A_{2}$ ， $B_{1}$ ， $B_{2}$ 为顶点， $F_{1}$ ， $F_{2}$ 为焦点，P为椭圆上一点，满足下列条件能使椭圆C为“黄金椭圆”的有（）

A、 ${| F_{1} F_{2} |}^{2} = | A_{1} F_{1} | \cdot | A_{2} F_{2} |$ B、 $∠ F_{1} B_{1} A_{2} = 90 °$ C、 $P F_{1} ⊥ x$ 轴，且 $P O ∥ A_{2} B_{1}$ D、四边形 $A_{1} B_{2} A_{2} B_{1}$ 的内切圆过焦点 $F_{1}$ ， $F_{2}$

查看试题解析
12. 已知点P是椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ 上一点， $F_{1}$ ， $F_{2}$ 是椭圆的左、右焦点，若 $∠ F_{1} P F_{2} = 60 °$ ，则下列说法正确的是（）

A、 $△ F_{1} P F_{2}$ 的面积为 $\frac{5 \sqrt{3}}{3}$ B、若点M是椭圆上一动点，则 $\vec{M F_{1}} \cdot \vec{M F_{2}}$ 的最大值为9 C、点P的纵坐标为 $\frac{5 \sqrt{3}}{6}$ D、 $△ F_{1} P F_{2}$ 内切圆的面积为 $\frac{π}{3}$

查看试题解析
13. 某房地产建筑公司在挖掘地基时，出土了一件宋代小文物，该文物外面是红色透明蓝田玉材质，里面是一个球形绿色水晶宝珠，其轴截面（如图）由半椭圆 $C_{1} ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (x \geq 0)$ 与半椭圆 $C_{2} ： \frac{x^{2}}{c^{2}} + \frac{y^{2}}{d^{2}} = 1 (x < 0)$ 组成，其中 $a^{2} = b^{2} + c^{2} ， a > b > c > 0$ ，设点 $F_{0} ， F_{1} ， F_{2}$ 是相应椭圆的焦点， $A_{1} ， A_{2}$ 和 $B_{1} ， B_{2}$ 是轴截面与 $x ， y$ 轴交点，阴影部分是宝珠轴截面，其以曲线 $x^{2} + y^{2} = 4$ 为边界， $F_{1} ， F_{2}$ 在宝珠珠面上， $△ F_{0} F_{1} F_{2}$ 为等边三角形，则以下命题中正确的是（）

A、椭圆 $C_{1}$ 的离心率是 $\frac{\sqrt{21}}{7}$ B、椭圆 $C_{2}$ 的离心率大于椭圆 $C_{1}$ 的离心率 C、椭圆 $C_{2}$ 的焦点在 $y$ 轴上 D、椭圆 $C_{2}$ 的长短轴之比大于椭圆 $C_{1}$ 的长短轴之比

查看试题解析
14. 某颗人造地球卫星的运行轨道是以地球的中心 $F$ 为一个焦点的椭圆，如图所示，已知它的近地点 $A$ （离地面最近的点）距地面 $m$ 千米，远地点 $B$ （离地面最远的点）距地面 $n$ 千米，并且 $F 、 A 、 B$ 三点在同一直线上，地球半径约为 $R$ 千米，设该椭圈的长轴长、短轴长、焦距分别为 $2 a 、 2 b 、 2 c$ ，则

A、 $a - c = m + R$ B、 $a + c = n + R$ C、 $2 a = m + n$ D、 $b = \sqrt{(m + R) (n + R)}$

查看试题解析
15. 已知椭圆 $E$ ： $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在 $E$ 上，若 $△ F_{1} P F_{2}$ 是直角三角形，则 $△ F_{1} P F_{2}$ 的面积可能为（）

A、5 B、4 C、 $\frac{4 \sqrt{5}}{3}$ D、 $\frac{2 \sqrt{5}}{3}$

查看试题解析

三、填空题

16. 已知水平地面上有一篮球，在斜平行光线的照射下，其阴影为一椭圆（如图），在平面直角坐标系中，椭圆中心 $O$ 为原点，设椭圆的方程为 $\frac{x^{2}}{m} + \frac{y^{2}}{n} = 1 (m > n > 0)$ ，篮球与地面的接触点为 $H$ ，则 $| O H |$ 的长等于.

查看试题解析
17. 已知 $F_{1}$ ， $F_{2}$ 是椭圆 $C ： \frac{x^{2}}{a^{2}} + y^{2} = 1 (a > 1)$ 的两个焦点，且椭圆上存在一点P，使得 $∠ F_{1} P F_{2} = \frac{2 π}{3}$ ，则椭圆C的离心率的最小值为．若点M，N分别是圆 $D ： x^{2} + {(y - 3)}^{2} = 3$ 和椭圆C上的动点，当椭圆C的离心率取得最小值时， $| M N | + | N F_{2} |$ 的最大值是．

查看试题解析
18. 古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积．若椭圆C的中心为原点，焦点 $F_{1} ， F_{2}$ 均在x轴上，C的面积为 $8 π$ ，且离心率为 $\frac{\sqrt{3}}{2}$ ，则C的标准方程为．

查看试题解析
19. 已知椭圆 $C_{1} ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $F_{1}$ 为左焦点， $A_{1}$ ， $A_{2}$ 为左、右顶点， $P$ 是椭圆 $C_{1}$ 上任意一点， $P F_{1}$ 的最大值为3，直线 $P A_{1}$ 和 $P A_{2}$ 满足 $k_{P A_{1}} k_{P A_{2}} = - \frac{3}{4}$ ，则椭圆 $C_{1}$ 的方程为，过 $P$ 作圆 $C_{2} ： x^{2} + {(y + 3 \sqrt{3})}^{2} = 3$ 的两条切线 $P M$ 、 $P N$ ，切点分别为 $M$ 、 $N$ 则 $\vec{C_{2} M} \cdot \vec{C_{2} N}$ 的最小值为．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ ，点M与C的焦点不重合，若M关于C的焦点的对称点分别为A，B，线段MN的中点在C上，则 $| A N | + | B N | =$ .

查看试题解析
21. 已知椭圆的方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ， $F_{1}$ ， $F_{2}$ 为椭圆的左右焦点，P为椭圆上在第一象限的一点，I为 $△ P F_{1} F_{2}$ 的内心，直线PI与x轴交于点Q，椭圆的离心率为 $\frac{1}{3}$ ，若 $\vec{P Q} = λ \vec{I Q}$ ，则 $λ$ 的值为.

查看试题解析
22. 已知 $F_{1} ， F_{2}$ 为椭圆C： $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ 的两个焦点，P ， Q为C上关于坐标原点对称的两点，且 $| P Q | = | F_{1} F_{2} |$ ，则四边形 $P F_{1} Q F_{2}$ 的面积为．

查看试题解析

2022年高考数学二轮复习 选择填空题型 17 椭圆

一、单选题

二、多选题

三、填空题

2022年高考数学二轮复习选择填空题型 17 椭圆