2022年高考数学二轮复习 选择填空题型 15 空间向量与空间几何
试卷更新日期:2022-01-10 类型:二轮复习
一、单选题
-
1. 在正三棱锥中,AB,AC,AD两两垂直,E,F分别是AB,AD的中点,过E,F的平面与棱AC交于点G,且(V表示体积),则AC与平面EFG所成角的正切值等于( )A、 B、 C、 D、2. 在长方体中, , , 点在上,点在上, , 则直线与所成角的余弦值为( )A、 B、 C、 D、3. 已知直线: , 下列结论正确的是( )A、直线的倾斜角为 B、直线的法向量为 C、直线的方向向量为 D、直线的斜率为4. 已知 , ,若 ,则 ( )A、9 B、6 C、5 D、35. 已知空间向量 , , 则向量在向量上的投影向量是( )A、 B、 C、 D、6. 在三棱锥 中, 平面 ,则二面角 的正切值为( )A、2 B、 C、3 D、7. 如图,四边形 为矩形, , 是 的中点,将 沿 翻折至 的位置(点 平面 ),设线段 的中点为 ,则在翻折过程中,下列论断不正确的是( )
 A、 平面 B、异面直线 与 所成角的大小恒定不变 C、 D、当平面 平面 时, 与平面 所成角为8. 若向量 、 满足 , ,则 在 方向上的投影为( )A、1 B、-1 C、 D、9. 已知底面 为正方形的四棱锥 , 点的射影在正方形 内,且 到 的距离等于 的长,记二面角 的平面角为 ,二面角 的平面角为 ,二面角 平面角为 ,则下列结论可能成立的是( )
A、 平面 B、异面直线 与 所成角的大小恒定不变 C、 D、当平面 平面 时, 与平面 所成角为8. 若向量 、 满足 , ,则 在 方向上的投影为( )A、1 B、-1 C、 D、9. 已知底面 为正方形的四棱锥 , 点的射影在正方形 内,且 到 的距离等于 的长,记二面角 的平面角为 ,二面角 的平面角为 ,二面角 平面角为 ,则下列结论可能成立的是( )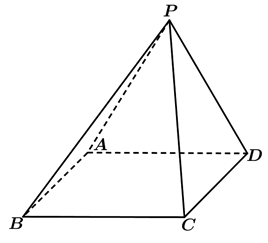 A、 B、 C、 D、10. 如图在底圆半径和高均为 的圆锥中, 、 是过底圆圆 的两条互相垂直的直径, 是母线 的中点,已知过 与 的平面与圆锥侧面的交线是以 为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点 的距离等于( ).
A、 B、 C、 D、10. 如图在底圆半径和高均为 的圆锥中, 、 是过底圆圆 的两条互相垂直的直径, 是母线 的中点,已知过 与 的平面与圆锥侧面的交线是以 为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点 的距离等于( ). A、 B、1 C、 D、
A、 B、1 C、 D、二、多选题
-
11. 八卦是中国文化的基本哲学概念,如图1船八卦模型图,其平面图形记为图2中的正八边形 , 其中 , 则下列结论正确的有( )
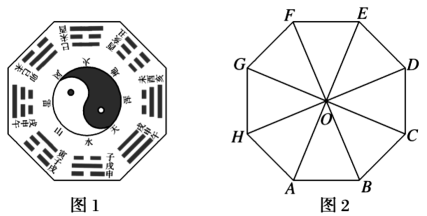 A、 B、 C、 D、在向量上的投影为12. 已知四面体的所有棱长均为2,则下列结论正确的是( )A、异面直线与所成角为 B、点A到平面的距离为 C、 D、四面体的外接球体积为13. 下列说法中错误的是( )A、已知 , ,则 与 可以作为平面内所有向量的一组基底 B、若 与 共线,则 在 方向上的投影为 C、若两非零向量 , 满足 ,则 D、平面直角坐标系中, , , ,则 为锐角三角形14. 已知 , ,则下列说法正确的有( )A、 在 方向上的投影为 B、与 同向的单位向量是 C、 D、 与 平行15. 已知正方体 中,点 为棱 的中点,点 是线段 上的动点, ,则下列选项正确的是( )A、直线 与 是异面直线 B、点 到平面 的距离是一个常数 C、过点 作平面 的垂线,与平面 交于点 ,若 ,则 D、若面 内有一点 ,它到 距离与到 的距离相等,则 轨迹为一条直线16. 在如图所示的几何体中,底面 是边长为4的正方形, 均与底面 垂直,且 ,点 分别为线段 的中点,则下列说法正确的是( )
A、 B、 C、 D、在向量上的投影为12. 已知四面体的所有棱长均为2,则下列结论正确的是( )A、异面直线与所成角为 B、点A到平面的距离为 C、 D、四面体的外接球体积为13. 下列说法中错误的是( )A、已知 , ,则 与 可以作为平面内所有向量的一组基底 B、若 与 共线,则 在 方向上的投影为 C、若两非零向量 , 满足 ,则 D、平面直角坐标系中, , , ,则 为锐角三角形14. 已知 , ,则下列说法正确的有( )A、 在 方向上的投影为 B、与 同向的单位向量是 C、 D、 与 平行15. 已知正方体 中,点 为棱 的中点,点 是线段 上的动点, ,则下列选项正确的是( )A、直线 与 是异面直线 B、点 到平面 的距离是一个常数 C、过点 作平面 的垂线,与平面 交于点 ,若 ,则 D、若面 内有一点 ,它到 距离与到 的距离相等,则 轨迹为一条直线16. 在如图所示的几何体中,底面 是边长为4的正方形, 均与底面 垂直,且 ,点 分别为线段 的中点,则下列说法正确的是( ) A、直线 与 所在平面相交 B、三棱锥 的外接球的表面积为 C、点C到平面 的距离为 D、二面角 中, 平面 平面 为棱 上不同两点, ,若 ,则17. 已知直三棱柱 中, , , 为 的中点.点 满足 ,其中 ,则( )A、对 时,都有 B、当 时,直线 与 所成的角是30° C、当 时,直线 与平面 所成的角的正切值 D、当 时,直线 与 相交于一点 ,则
A、直线 与 所在平面相交 B、三棱锥 的外接球的表面积为 C、点C到平面 的距离为 D、二面角 中, 平面 平面 为棱 上不同两点, ,若 ,则17. 已知直三棱柱 中, , , 为 的中点.点 满足 ,其中 ,则( )A、对 时,都有 B、当 时,直线 与 所成的角是30° C、当 时,直线 与平面 所成的角的正切值 D、当 时,直线 与 相交于一点 ,则三、填空题
-
18. 如图,已知三棱柱 各棱长均相等, ,则异面直线 与 所成角的大小是 , 二面角 的平面角的正弦值是 .
 19. 如图,已知平面四边形 中,△ 是边长为2的正三角形, ,以 为棱折成直二面角 ,若折叠后 , , , 四点在同一球面上,则该球的体积为.
19. 如图,已知平面四边形 中,△ 是边长为2的正三角形, ,以 为棱折成直二面角 ,若折叠后 , , , 四点在同一球面上,则该球的体积为.
 20. 如图,在边长为2的正方形 中, 、 分别是 、 的中点.若沿 、 及 把这个正方形折成一个四面体,使 、 、 三点重合,重合后的点记为 ,则:
20. 如图,在边长为2的正方形 中, 、 分别是 、 的中点.若沿 、 及 把这个正方形折成一个四面体,使 、 、 三点重合,重合后的点记为 ,则: (1)、三棱锥 外接球的表面积为;(2)、点 到平面 的距离为.
(1)、三棱锥 外接球的表面积为;(2)、点 到平面 的距离为.
