陕西省中考数学历年真题模拟题汇编——图形的相似
试卷更新日期：2022-01-10 类型：二轮复习
一、单选题
-
1. 《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中的第一问：今有望海岛，立两表，齐高三丈，前后相去千步，令后表与前表参相直.从前表却行一百二十三步，人目着地取望岛峰，与表末参合.从后表却行一百二十七步，人目着地取望岛峰，亦与表末参合.问岛高及去表各几何？大致意思是：假设测量海岛，立两根表，高均为3丈，前后相距1000步，令后表与前表在同一直线上，从前表退行123步，人的眼睛贴着地面观察海岛，从后表退行127步，人的眼睛贴着地面观察海岛，问海岛高度及两表相距多远？想要解决这一问题，需要利用（ ）A、全等三角形 B、相似三角形 C、勾股定理 D、垂径定理2. 如图，已知 ，且 ，则 （ ）
A、 B、 C、 D、3. 如图，在边长为12的正方形ABCD中，有一个小正方形EFGH，其中E、 F、G分别在AB、BC、FD上，若BF=3，则小正方形边长为（ ）
A、6 B、5 C、 D、4. 如图，在矩形ABCD中，BC＝8，对角线AC与BD相交于点O，过点D作AC的垂线DE，交AC于点E，AE＝3CE.则DE的值为（ ）
A、4 B、2 C、4 D、25. 如图，∠ACB＝90°，D为AB中点，连接DC并延长到点E，使CE＝ CD，过点B作BF∥DE交AE的延长线于点F.若BF＝10，则AB的长为（ ）
A、12 B、10 C、8 D、56. 如图，点E是平行四边形ABCD中BC的延长线上的一点，连接AE交CD于F，交BD于M，则图中共有相似三角形(不含全等的三角形)（ ）对.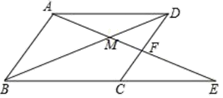
A、4 B、5 C、6 D、77. 如图，E是矩形ABCD中AD边的中点，BE交AC于点 的面积为2，则四边形CDEF的面积为（ ）
A、4 B、5 C、6 D、78. 如图，在 中， ， 则DF的长为（ ）
A、4 B、 C、 D、39. 如图，在矩形ABCD中，点E在AB上，点F在CD上，且BE=2AE，DF=2CF，G，H是对角线AC的三等分点。若四边形EGFH的面积为2，则矩形ABCD的面积为（ ）
A、36 B、24 C、18 D、1210. 如图，在矩形ABCD中，AB=3，BC=6，若点E，F分别在AB，CD上，且BE=2AE，DF=2FC，G，H分别是AC的三等分点，则四边形EHFG的面积为（ ）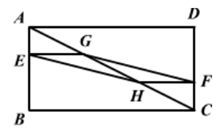
A、1 B、 C、2 D、4二、填空题
-
11. 如图， 的顶点O在坐标原点上， ，若点B在反比例函数 的图象上，点A在反比例函数 的图象上，则k的值为.
12. 如图，矩形ABCD中，M为边AD上的一点.将△CDM沿CM折叠，得到△CMN，若AB＝6，DM＝2，则N到AD的距离为.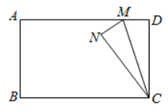
13. 如图，在平面直角坐标系中，过原点的直线与反比例函数 交于点A，与反比例函数 交于点B，过点A作x轴的垂线，过点B作y轴的垂线，两直线交于点C，若 的面积为9，则k的值为.
14. 如图，在 中， ， ， ，点F在边AC上，点E为边BC上的动点，将 沿直线EF翻折，点C落在点P处.若 ，则点P到AB距离的最小值为.
15. 如图，已知，在矩形AOBC中，OB=4，OA=3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点(不与B、C重合)，过F点的反比例函数y (k＞0)的图象与AC边交于点E，将△CEF沿E对折后，C点恰好落在OB上的点D处，则k的值为.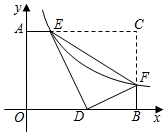
16. 如图，在矩形 中， ，E是CD延长线上一点，连接BE交AD于点F，连接CF，若 与 的面积相等，则DE长为.
17. 如图，已知点A、B分别在反比例函数y= (x>0)，y= (x<0)的图象上，且OA⊥OB，则OA：OB的值为。
18. 如图，在平面直角坐标系中，O为坐标原点，▱ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限.将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F.若y＝ （k≠0）图象经过点C，且S△BEF＝ ，则k的值为.
19. 如图，在平行四边形ABCD中，AB=4，BC=5，∠ABC=60°，平行四边形ABCD的对角线AC，BD交于点O，过点O作OE⊥AD，则OE=.
20. 如图，在△ABC中，D、E、F分别为边AB、AC、BC上的点，连接DE、EF。若DE∥BC，EF∥AB，则图中共有对相似三角形.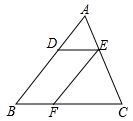
21. 如图，在正方形ABCD中，AB=8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM=6. P为对角线BD上一点，则PM—PN的最大值为.
三、作图题
-
22. 如图，已知在正方形ABCD中，M是BC边上一定点，连接AM，请用尺规作图法，在AM上求作一点P，使得△DPA∽△ABM（不写做法保留作图痕迹）
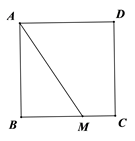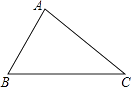
23.如图，已知△ABC，∠BAC=90°，请用尺规过点A作一条直线，使其将△ABC分成两个相似的三角形（保留作图痕迹，不写作法）
四、解答题
-
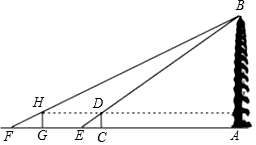
24. 西安市的大雁塔又名“慈恩寺塔”，是国家级文物保护单位，玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔，最初五层，后加盖至九层，是西安市的标志性建筑之一，某校社会实践小组为了测量大雁塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，大雁塔的塔尖点B正好在同一直线上，测得EC=4米，将标杆CD向后平移到点G处，这时地面上的点F，标杆的顶端点H，大雁塔的塔尖点B正好在同一直线上(点F，点G，点E，点C与塔底处的点A在同一直线上)，这时测得FG=6米，GC=53米，请你根据以上数据，计算大雁塔的高度AB.
25. 为了测量路灯（OS）的高度，把一根长1.5米的竹竿（AB）竖直立在水平地面上，测得竹竿的影子（BC）长为1米，然后拿竹竿向远离路灯方向走了4米（BB′），再把竹竿竖立在地面上，测得竹竿的影长（B′C′）为1.8米，求路灯离地面的高度.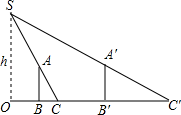
26. 周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D竖起标杆DE，使得点E与点C、A共线．已知：CB⊥AD，ED⊥AD，测得BC＝1m，DE＝1.5m，BD＝8.5m．测量示意图如图所示．请根据相关测量信息，求河宽AB．
五、综合题
-
27. 如图， 为 的直径， 、 是 的两条弦， 是 的切线，且 交 于点D.
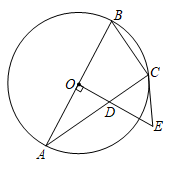(1)、求证： .(2)、若 的半径为8， ，求弦 的长.28. 如图，等腰 ，AC=BC＞AB，射线AD与BC交于点D.
(1)、在射线AD上求作一点E，使得∠CAE=∠AEB；(要求：尺规作图，保留作图痕迹，不写作法)(2)、在（1）的条件下，若CD=2BD，AC=12，求BE的值.29. 如图，直线AM与⊙O相切于点A，弦BC AM，连接BO并延长，交⊙O于点E，交AM于点F，连接CE并延长，交AM于点D.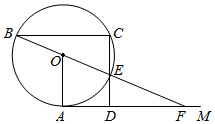
(1)、求证：CE OA；(2)、若⊙O的半径R＝13，BC＝24，求AF的长.30. 综合题(1)、问题提出如图①，△ABC是等边三角形，AB=12，若点O是△ABC的内心，则OA的长为；
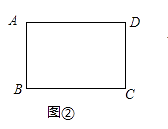
(2)、问题探究如图②，在矩形ABCD中，AB=12，AD=18，如果点P是AD边上一点，且AP=3，那么BC边上是否存在一点Q，使得线段PQ将矩形ABCD的面积平分？若存在，求出PQ的长；若不存在，请说明理由．
(3)、问题解决某城市街角有一草坪，草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在M处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于∠AMB（即每次喷灌时喷灌龙头由MA转到MB，然后再转回，这样往复喷灌．）同时，再合理设计好喷灌龙头喷水的射程就可以了．
如图③，已测出AB=24m，MB=10m，△AMB的面积为96m2；过弦AB的中点D作DE⊥AB交 于点E，又测得DE=8m．
请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到0.01米）
31.如图，已知：AB是⊙O的弦，过点B作BC⊥AB交⊙O于点C，过点C作⊙O的切线交AB的延长线于点D，取AD的中点E，过点E作EF∥BC交DC的延长线于点F，连接AF并延长交BC的延长线于点G．
求证：
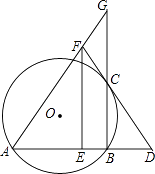(1)、FC=FG；(2)、AB2=BC•BG．