浙教版备考2022年中考数学一轮复习专题35 图形的对称、平移与旋转
试卷更新日期:2022-01-10 类型:一轮复习
一、单选题
-
1. 下图是设计师石昌鸿设计的《魅力中国》部分城市字体,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是( )
2. 如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PB=BC,则下列四种不同方法的作图中,作法正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、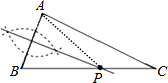 3. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=10 m,且tan∠CEF= ,那么矩形ABCD的面积为( )cm2;
3. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=10 m,且tan∠CEF= ,那么矩形ABCD的面积为( )cm2;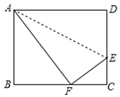 A、280 B、300 C、320 D、3604. 在平面直角坐标系中,已知点P1(﹣5,3)和P2(﹣5,﹣3),则P1和P2( )A、关于原点对称 B、关于y轴对称 C、关于x轴对称 D、不存在对称关系5. 已知点P(3,2x﹣4)关于x轴的对称点在第一象限,则x的取值范围是( )A、x>2 B、x<2 C、x>0 D、x<06. 若点P(﹣2,3)关于y轴的对称点为Q(a , b),则点为Q坐标为( )A、(﹣2,﹣3) B、(2,3) C、(2,﹣3) D、(﹣2,3)7. 下列图形:线段、角、正方形、圆,其中是轴对称图形个数的为( )A、1 B、2 C、3 D、48. 如下图,将三角形绕轴旋转一周,所得的立体图形从正面观察得到的图形是( )
A、280 B、300 C、320 D、3604. 在平面直角坐标系中,已知点P1(﹣5,3)和P2(﹣5,﹣3),则P1和P2( )A、关于原点对称 B、关于y轴对称 C、关于x轴对称 D、不存在对称关系5. 已知点P(3,2x﹣4)关于x轴的对称点在第一象限,则x的取值范围是( )A、x>2 B、x<2 C、x>0 D、x<06. 若点P(﹣2,3)关于y轴的对称点为Q(a , b),则点为Q坐标为( )A、(﹣2,﹣3) B、(2,3) C、(2,﹣3) D、(﹣2,3)7. 下列图形:线段、角、正方形、圆,其中是轴对称图形个数的为( )A、1 B、2 C、3 D、48. 如下图,将三角形绕轴旋转一周,所得的立体图形从正面观察得到的图形是( )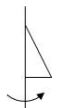 A、
A、 B、
B、 C、
C、 D、
D、 9. 下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )A、
9. 下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D,延长 交 于点F,则下列结论一定正确的是( )
10. 如图,在 中, ,将 绕点C顺时针旋转得到 ,使点B的对应点E恰好落在边 上,点A的对应点为D,延长 交 于点F,则下列结论一定正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在平面直角坐标系 中, 可以看作是 经过若干次的图形变化(轴对称、平移)得到的,写出一种由 得到 的过程: .
 12. 在平面直角坐标系中,将点P(﹣1,2)向右平移3个单位得到点Q , 则点Q的坐标为 .13. 平面直角坐标系中三个点O(0,0),4(﹣1,1),B(﹣1,0),将△ABO绕点O按顺时针旋转135°,则点B的对应点B1的坐标是 .14. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .
12. 在平面直角坐标系中,将点P(﹣1,2)向右平移3个单位得到点Q , 则点Q的坐标为 .13. 平面直角坐标系中三个点O(0,0),4(﹣1,1),B(﹣1,0),将△ABO绕点O按顺时针旋转135°,则点B的对应点B1的坐标是 .14. 如图,正方形 的对角线相交于点 ,点 是正方形 的一个顶点,如果两个正方形的边长相等,正方形 绕点 自由转动,设两个正方形重叠部分(阴影)的面积为 ,正方形 的面积为 .则 与 的关系是 .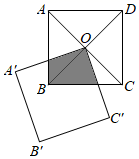 15. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 , ,依此类推,则点 的坐标为 .
15. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 , ,依此类推,则点 的坐标为 .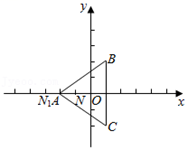 16. 如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连结EF.已知 , , 则EF的长为 .
16. 如图,矩形ABCD中,BD为对角线,将矩形ABCD沿BE、BF所在直线折叠,使点A落在BD上的点M处,点C落在BD上的点N处,连结EF.已知 , , 则EF的长为 .
三、综合题
-
17. 如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,A(-3,2),B(-4,-3),C(﹣1,﹣1).
 (1)、画出 关于y轴对称的图形 ;(2)、写出 、 、 的坐标(直接写出答案) ; ; ;(3)、写出 的面积为 . (直接写出答案)(4)、在y轴上求作一点 P,使得点P到点A与点C的距离之和最小.18. 在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).
(1)、画出 关于y轴对称的图形 ;(2)、写出 、 、 的坐标(直接写出答案) ; ; ;(3)、写出 的面积为 . (直接写出答案)(4)、在y轴上求作一点 P,使得点P到点A与点C的距离之和最小.18. 在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1). (1)、在图中作出△ABC关于y轴的对称△A1B1C1 .(2)、写出△ABC关于x轴对称△A2B2C2的各顶点坐标.
(1)、在图中作出△ABC关于y轴的对称△A1B1C1 .(2)、写出△ABC关于x轴对称△A2B2C2的各顶点坐标.A2 B2 C2
19. 如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(﹣4,1),B(﹣3,﹣4). (1)、将线段AB向上平移2个单位,再向右平移5个单位得到线段A′B′,画出线段A′B′(点A′,B′分别为A , B的对应点);(2)、若点P(m , n)为线段AB上任意一点,经过(1)的平移后,在线段A′B′上对应的点P′的坐标为 ;(3)、△B′AB的面积为 .20. 如图,在正方形网格中,点A、B、C、M、N都在格点上.
(1)、将线段AB向上平移2个单位,再向右平移5个单位得到线段A′B′,画出线段A′B′(点A′,B′分别为A , B的对应点);(2)、若点P(m , n)为线段AB上任意一点,经过(1)的平移后,在线段A′B′上对应的点P′的坐标为 ;(3)、△B′AB的面积为 .20. 如图,在正方形网格中,点A、B、C、M、N都在格点上. (1)、作△ABC关于直线MN对称的图形△A′B′C′.(2)、若网格中最小正方形的边长为1,求△ABC的面积.21. 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数 表示的点重合,则数轴上数 表示的点与数4表示的点重合.
(1)、作△ABC关于直线MN对称的图形△A′B′C′.(2)、若网格中最小正方形的边长为1,求△ABC的面积.21. 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数 表示的点重合,则数轴上数 表示的点与数4表示的点重合.
根据你对例题的理解,解答下列问题:
若数轴上数 表示的点与数1表示的点重合.(根据此情境解决下列问题)
(1)、则数轴上数3表示的点与数表示的点重合;(2)、若点 到原点的距离是5个单位长度,并且 、 两点经折叠后重合,则 点表示的数是;(3)、若数轴上 、 两点之间的距离为2020(点M在点N的右侧),并且 、 两点经折叠后重合,则 点表示的数是 , 则 点表示的数是 .22. 如图,方格纸中每个小方格都是边长为1个单位的正方形,已知 的三个顶点在格点上. (1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小23. 当图形具有邻边相等的特征时,我们可以把图形的一部分绕着公共端点旋转,这样将分散的条件集中起来,从而达到解决问题的目的.
(1)、画出 ,使它与 关于直线a对称;(2)、求出 的面积;(3)、在直线a上画出点P,使 最小23. 当图形具有邻边相等的特征时,我们可以把图形的一部分绕着公共端点旋转,这样将分散的条件集中起来,从而达到解决问题的目的. (1)、如图1,等腰直角三角形ABC内有一点P,连接AP,BP,CP,∠APB=135°,为探究AP,BP,CP三条线段间的数量关系,我们可以将△ABP,绕点A逆时针旋转90°得到△ACP',连接PP',则PP'=AP,△CPP'是三角形,AP,BP,CP三条线段的数量关系是 .(2)、如图2,等边三角形ABC内有一点P,连接AP、BP、CP,∠APB=150°,请借助第一问的方法探究AP、BP、CP三条线段间的数量关系.(3)、如图3,在四边形ABCD中,AD∥BC,点P在四边形的内部,且PD=PC,∠CPD=90°,∠APB=135°,AD=4,BC=5,请直接写出AB的长.24. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
(1)、如图1,等腰直角三角形ABC内有一点P,连接AP,BP,CP,∠APB=135°,为探究AP,BP,CP三条线段间的数量关系,我们可以将△ABP,绕点A逆时针旋转90°得到△ACP',连接PP',则PP'=AP,△CPP'是三角形,AP,BP,CP三条线段的数量关系是 .(2)、如图2,等边三角形ABC内有一点P,连接AP、BP、CP,∠APB=150°,请借助第一问的方法探究AP、BP、CP三条线段间的数量关系.(3)、如图3,在四边形ABCD中,AD∥BC,点P在四边形的内部,且PD=PC,∠CPD=90°,∠APB=135°,AD=4,BC=5,请直接写出AB的长.24. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C在小正方形的顶点上. (1)、在图中画出与 ABC关于直线l成轴对称的(2)、四边形 的面积为;(3)、在直线l上找一点P,使PA+PB的长最短.25. 在平面直角坐标系xOy中, ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).(1)、点C关于x轴对称的点C1的坐标为 , 点C关于y轴对称的点C2的坐标为 .(2)、试说明 ABC是直角三角形.(3)、已知点P在x轴上,若 ,求点P的坐标.26. 如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕.请回答下列问题:
(1)、在图中画出与 ABC关于直线l成轴对称的(2)、四边形 的面积为;(3)、在直线l上找一点P,使PA+PB的长最短.25. 在平面直角坐标系xOy中, ABC三个顶点的坐标分别为A(0,2),B(2,0),C(5,3).(1)、点C关于x轴对称的点C1的坐标为 , 点C关于y轴对称的点C2的坐标为 .(2)、试说明 ABC是直角三角形.(3)、已知点P在x轴上,若 ,求点P的坐标.26. 如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕.请回答下列问题: (1)、AF=;(2)、试求线段DE的长度.27. 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②).
(1)、AF=;(2)、试求线段DE的长度.27. 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图②). (1)、在上述旋转过程中,BH与CK有怎样的数量关系四边形CHGK的面积有何变化?证明你发现的结论;(2)、连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)、在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的 ?若存在,求出此时x的值;若不存在,说明理由.28. 如图,在平面直角坐标系中, 的顶点 , , 均在正方形网格的格点上.
(1)、在上述旋转过程中,BH与CK有怎样的数量关系四边形CHGK的面积有何变化?证明你发现的结论;(2)、连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)、在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的 ?若存在,求出此时x的值;若不存在,说明理由.28. 如图,在平面直角坐标系中, 的顶点 , , 均在正方形网格的格点上. (1)、画出 关于 轴的对称图形 .(2)、将 沿 轴方向向左平移 个单位后得到 ,写出顶点 , , 的坐标.(3)、求 的面积.29. 在 中, , ,点P为直线BC上一动点(不与点B、C重合),连接AP,将线段AP所在的直线绕点P顺时针旋转 得到直线PM,再将线段AC所在的直线绕点C顺时针旋转 得到直线CN,直线PM与直线CN相交于点Q.
(1)、画出 关于 轴的对称图形 .(2)、将 沿 轴方向向左平移 个单位后得到 ,写出顶点 , , 的坐标.(3)、求 的面积.29. 在 中, , ,点P为直线BC上一动点(不与点B、C重合),连接AP,将线段AP所在的直线绕点P顺时针旋转 得到直线PM,再将线段AC所在的直线绕点C顺时针旋转 得到直线CN,直线PM与直线CN相交于点Q. (1)、当点P在线段BC上,当 时,如图1,直接判断 的大小,(2)、当点P在线段BC上,当 时,如图2,试判断线段 的大小,并说明理由;(3)、当点P在直线BC上,当 , , 时,请利用备用图探究 面积的大小(直接写出结果即可).
(1)、当点P在线段BC上,当 时,如图1,直接判断 的大小,(2)、当点P在线段BC上,当 时,如图2,试判断线段 的大小,并说明理由;(3)、当点P在直线BC上,当 , , 时,请利用备用图探究 面积的大小(直接写出结果即可).