浙教版备考2022年中考数学一轮复习专题34 命题与证明

试卷更新日期：2022-01-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列选项中，可以用来证明命题“若x² $>$ 9，则x $>$ 3”是假命题的反例是（）

A、x $=$ 3 B、x $=$ -3 C、x $=$ 4 D、x $=$ -4

查看试题解析
2. 在探究证明“三角形的内角和是180°”时，综合实践小组的同学作了如下四种辅助线，其中不能证明“三角形内角和是180°”的是（）

A、 B、 C、 D、

查看试题解析
3. 下列命题中正确的有（）个
⑴有两个角互余的三角形是直角三角形；（2）有一个角等于60°的等腰三角形是等边三角形；（3）等腰三角形的角平分线、中线、高互相重合；（4）在角的内部，到角的两边距离相等的点在这个角的平分线上．

A、1 B、2 C、3 D、4

查看试题解析
4. 下列说法正确的是（）

A、所有的整数都是正数 B、正数和负数统称有理数 C、零不是正数，也不是负数，但是整数 D、没有最大的正整数，也没有最大的负整数

查看试题解析
5. 给出下列各说法：
①圆柱由3个面围成，这3个面都是平的；②圆锥由2个面围成，这2个面中，1个是平的，1个是曲的；③球仅由1个面围成，这个面是平的；④正方体由6个面围成，这6个面都是平的．其中正确的为（）

A、①② B、②③ C、②④ D、③④

查看试题解析
6. 如图，点 $B$ 、 $C$ 、 $D$ 在同一条直线上，则下列说法正确的是（）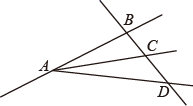

A、射线 $B D$ 和射线 $D B$ 是同一条射线 B、直线 $B C$ 和直线 $C D$ 是同一条直线 C、图中只有 $4$ 条线段 D、图中有 $4$ 条直线

查看试题解析
7. 下列命题中，是真命题的是（）

A、同位角相等 B、同角的余角相等 C、相等的角是对顶角 D、有且只有一条直线与已知直线垂直

查看试题解析
8. 下列有四个结论，其中正确的是（）
①若 ${(x - 1)}^{x + 1} = 1$ ，则 $x$ 只能是 $2$ ；②若 $(x - 1) (x^{2} + a x + 1)$ 的运算结果中不含 $x^{2}$ 项，则 $a = 1$ ③若 $a + b = 10$ ， $a b = 2$ ，则 $a - b = 2$ ④若 $4^{x} = a$ ， $8^{y} = b$ ，则 $2^{2 x - 3 y}$ 可表示为 $\frac{a}{b}$

A、①②③④ B、②③④ C、①③④ D、②④

查看试题解析
9. 下列各说法中：①圆的每一条直径都是它的对称轴；②长度相等的两条弧是等弧；③相等的弦对的弧也相等；④平分弦的直径垂直于弦；⑤90°的圆周角所对的弦是直径；⑥任何一个三角形都有唯一的外接圆；其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 下列语句中，是命题的是（）

A、延长线段 $A B$ 到 $C$ B、垂线段最短 C、画 $∠ A O B = 45 °$ D、等角的余角相等吗？

查看试题解析

二、填空题

11. 用反证法证明“已知，a⊥b，c⊥b，求证：a∥c”，第一步应先假设．

查看试题解析
12. 命题“如果ab＝0，那么a+b＝0”的逆命题为．

查看试题解析
13. 三个互不相等的有理数，既可以表示为1， $a + b$ ， $a$ ，也可以表示为0， $\frac{a}{b}$ ， $b$ ，则 $b$ = ．

查看试题解析
14. 下列语句：①没有绝对值为﹣3的数；②﹣a是一个非正数；③倒数等于它本身的数是1；④单项式6×10⁴x²的系数是6；⑤x﹣3xy＋2y是二次三项式．其中正确的有．

查看试题解析
15. 写出命题“等腰三角形的两个底角相等”的逆命题：．

查看试题解析
16. 用反证法证明命题“如果a $\geq$ b， b $\geq$ c，那么a $\geq$ c”时，应假设.

查看试题解析

三、综合题

17. 如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．

(1)、求证：四边形AFBD是平行四边形；

(2)、将下列命题填写完整，并使命题成立（图中不再添加其它的点和线）：
①当△ABC满足条件AB＝AC时，四边形AFBD是形；

② 当△ABC满足条件时，四边形AFBD是正方形．

查看试题解析
18.

(1)、如图1，在△ABC中，D是AB上一点，E是AC上一点，BE、CD相交于点F ， ∠A＝62°，∠ACD＝35°，∠ABE＝20°．求：∠BFD的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．

解：∵∠BDC＝∠A+∠ACD（ ▲ ），

∴∠BDC＝62°+35°＝97°（等量代换）．

∵∠BFD+∠BDC+∠ABE＝ ▲ （ ▲ ），

∴∠BFD＝180°﹣∠BDC﹣∠ABE＝180°﹣97°﹣20°＝63°（等式的性质）．

(2)、如图2，把一个长方形的纸ABCD沿对角线折叠（长方形对边平行且相等，四个角是直角），重合部分△FBD是个什么三角形？请证明你的结论．

查看试题解析
19. 如图1所示， $∠ A O B$ 、 $∠ C O D$ 都是直角．

(1)、试猜想 $∠ A O D$ 与 $∠ C O B$ 在数量上的关系是相等、互余还是互补的关系？你能用推理的方法说明你的猜想是否正确吗？

(2)、当 $∠ C O D$ 绕着点O旋转到图2的位置时，你原来的猜想还成立吗？

查看试题解析
20. 课本指出：公认的真命题称为基本事实，除了基本事实外，其他的真命题（如推论、定理等）的符合题意性都需要借助基本事实，通过推理的方法证实．例如：我们学过三角形全等的基本事实有三个，即：“ $SSS$ ”、“ $SAS$ ”、“ $ASA$ ”，请你完成以下问题：

(1)、叙述三角形全等的判定方法中的推论 $AAS$ ：如果两个三角形的及其中一个对应相等，那么这两个三角形全等．

(2)、小红同学对这个推论的符合题意性进行了证明，她画出了 $△ A B C$ 和 $△ D E F$ ，并写出了如下不完整的已知和求证：
已知：如图， $△ A B C$ 和 $△ D E F$ 中，

$∠ B = ∠ E$ ， $∠ A =$ ， $= E F$

求证： $△ A B C ≌ △ D E F$

(3)、按小红的想法写出证明：

证明：

查看试题解析
21. 已知：如图， $△$ ABC为锐角三角形，AB=AC，CD∥AB．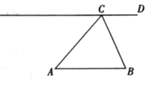

求作：线段BP，使得点P在直线CD上，且∠ABP= $\frac{1}{2} ∠ B A C$ ．

作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）

(2)、完成下面的证明．
证明：∵CD∥AB，

∴∠ABP= ．

∵AB=AC，

∴点B在⊙A上．

又∵∠BPC= $\frac{1}{2}$ ∠BAC（）（填推理依据）

∴∠ABP= $\frac{1}{2}$ ∠BAC

查看试题解析
22. 探究问题：已知∠ABC ，画一个角∠DEF ，使DE∥AB ， EF∥BC ，且DE交BC于点P ． ∠ABC与∠DEF有怎样的数量关系？

(1)、我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．
①图1中∠ABC与∠DEF数量关系为；图2中∠ABC与∠DEF数量关系为；

请选择其中一种情况说明理由．

②由①得出一个真命题（用文字叙述）：．

(2)、应用②中的真命题，解决以下问题：
若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．

查看试题解析
23. 推理说明．

(1)、如图1，两条直线相交形成四个角，可以用推理说明图中的 $∠ 1 = ∠ 3$ ．请在括号内填写推理的依据．
推理过程：

因为： $∠ 1 + ∠ 2 = 180 °$ ， $∠ 3 + ∠ 2 = 180 °$ （）

所以： $∠ 1 + ∠ 2 = ∠ 3 + ∠ 2$

也就有 $∠ 1 = ∠ 3$ （）

(2)、如图2，把三角形 $A B C$ 的边 $B C$ 延长到点 $D$ ，请你用推理说明： $∠ 1 + ∠ 2 = ∠ 4$ ．

查看试题解析
24. 小亮同学要证明命题“对角线互相垂直平分的四边形是菱形”是正确的，他先用尺规作出了如图的四边形 $A B C D$ ，并写出了如下不完整的已知和求证.

(1)、已知：如图，在四边形 $A B C D$ 中， $A C ⊥ B D$ ，垂足为O， $O A = O C$ ，.

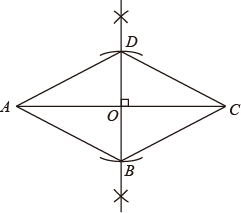(2)、求证：四边形 $A B C D$ 是.

(3)、填空，补全已知和求证；
写出证明过程；

(4)、用文字叙述所证命题的逆命题为.

查看试题解析
25. 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD，并写出了如下不完整的已知和求证．

已知：如图，在四边形ABCD中，

BC=AD，

AB=____________，

求证：四边形ABCD是_________________四边形。

(1)、在方框中填空，以补全已知和求证；

(2)、按嘉淇同学的想法写出证明；
证明：

(3)、用文字叙述所证命题的逆命题为

查看试题解析

26. 阅读下列材料，完成相应的任务

婆罗摩笈多（Brahmagupta）是古印度著名数学家、天文学家，他在三角形、四边形、零和负数的算术运算规则、二次方程等方面均有建树，特别是在研究一阶和二阶不定方程方面作出了巨大贡献．他曾经提出了“婆罗摩笈多定理”，该定理也称为“古拉美古塔定理”．该定理的内容及部分证明过程如下：

古拉美古塔定理：已知：如图，四边形ABCD内接于⊙O，对角线AC⊥BD，垂足为M，直线ME⊥BC，垂足为E，并且交直线AD于点F，则AF＝FD．

证明：∵AC⊥BD，ME⊥BC

∴∠CME+∠C＝90°，∠CBD+∠C＝90°

∴∠CBD＝∠CME

∴ ，∠CME＝∠AMF

∴∠CAD＝∠AMF

∴AF＝MF

…

任务：

(1)、材料中划横线部分短缺的条件为：；

(2)、请用符号语言将下面“布拉美古塔定理”的逆命题补充完整，并证明该逆命题的符合题意性：

已知：如图，四边形ABCD内接于⊙O，对角线AC⊥BD，垂足为M，F为AD上一点，直线FM交BC于点E，

① ▲ ．

求证：② ▲ ．

证明：

查看试题解析

27. 已知： $△ A B C$ ，CD平分 $∠ A C B$ ．
求作：菱形DFCE ，使点F在BC边上，点E在AC边上，下面是尺规作图过程．

作法：①分别以C、D为圆心，大于 $\frac{1}{2} C D$ 为半径作弧，两弧分别交于点M、N；

②作直线MN分别与AC、BC交于点E、F；

③连接DE、DF ， DC与EF的交点记为点G；四边形DFCE为所求作的菱形．

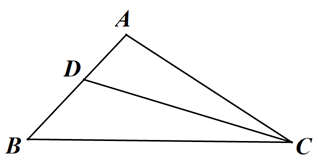(1)、利用直尺和圆规依做法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明： $∵ D E = E C ， D F = F C$ ，

$∴ E F$ 为DC的垂直平分线．

$∵ D E = E C$ ，

$∴ ∠ E D C = ∠ E C D$ ．

$∵ C D$ 平分 $∠ A C B$ ，

$∴ ∠ E C D = ∠ D C B$ ．

$∴ ∠ E D C = ∠ D C B$ ，

$∴$ ▲ $/ /$ ▲ （）（填推理依据）

同理可证 $E F / / C E$ ，

$∴$ 四边形DFCE为平行四边形．

又 $∵$ ▲ ，

$∴$ 四边形DFCE为菱形．

查看试题解析
28. 将一块 $a \times b \times c (a < b < c)$ 的长方体铁块（图1）平放在一个长方体水槽底部（图2），现向水槽内匀速注水，直至注满水槽为止，因铁块在水槽内有3种不同的放置方式，所以水槽内的水深h与注水时间t的函数关系用图象来反映，其全过程有三种不同的图象（图3，图4，图5）（注：长度单位：厘米；时间单位：秒）

(1)、判断t₁与t₂的大小关系：t₁t₂；

(2)、水槽深度为厘米；a=厘米，b=厘米；

(3)、求铁块的体积.

查看试题解析