浙教版备考2022年中考数学一轮复习专题33 弧长与扇形

试卷更新日期：2022-01-10 类型：一轮复习

进入出卷网下载

一、单选题

1. 如图，⊙O是△ABC的外接圆，BC＝2，∠BAC＝30°，则劣弧 $\overset{⌢}{B C}$ 的长等于（）

A、 $\frac{2 π}{3}$ B、 $\frac{π}{3}$ C、 $\frac{2 \sqrt{3} π}{3}$ D、 $\frac{\sqrt{3} π}{3}$

查看试题解析
2. 已知圆心角为120°的扇形的面积为12π，则扇形的弧长为（）

A、4π B、2π C、4 D、2

查看试题解析
3. 如图，在5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与BD交于E，则图中阴影部分的面积为（）（结果保留π）

A、 $\frac{5}{4}$ π- $\frac{5}{8}$ B、 $\frac{5}{3}$ C、 $\frac{13}{16}$ π- $\frac{13}{8}$ D、 $\frac{5}{3}$ π

查看试题解析
4. 如图，四边形ABCD是⊙O的内接四边形，∠ABC＝2∠D，∠AOB＝ $\frac{1}{3}$ ∠COB，⊙O的半径为 $\sqrt{3}$ ，连接AC交OB于点E，则图中阴影部分面积是（）

A、 $\frac{3 π}{4} - \frac{3}{2}$ B、 $\frac{\sqrt{3} π}{4} - \frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3} π}{4} - \sqrt{3}$ D、 $\frac{3 π}{4} - \frac{\sqrt{3}}{2}$

查看试题解析
5. 如图物体由两个圆锥组成．其主视图中，∠A＝90°，∠ABC＝105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（）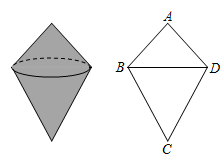

A、2 B、 $\sqrt{3}$ C、 $\frac{3}{2}$ D、 $\sqrt{2}$

查看试题解析
6. 如图，圆锥的轴截面是一个斜边为2cm的等腰直角三角形，则这个圆锥的侧面积是（）

A、 $\frac{\sqrt{2}}{2} π {cm}^{2}$ B、 $\sqrt{2} π {cm}^{2}$ C、 $2 π {cm}^{2}$ D、 $2 \sqrt{2} π {cm}^{2}$

查看试题解析
7. 如图是一个几何体的三视图，根据图中所标数据计算这个几何体的体积为（）

A、 $12 π$ B、 $18 π$ C、 $24 π$ D、 $30 π$

查看试题解析
8. 如图，在四边形ABCD中，BC=CD=4，AB=7，AB⊥BC，CD⊥BC。把四边形ABCD绕AB旋转一周，则该几何体的表面积为（）

A、48π B、56π C、68π D、72π

查看试题解析
9. 如图，AB为半圆O的直径，C是半圆上一点，且∠COA＝60°，设扇形AOC、△COB，弓形BmC的面积为S₁、S₂、S₂ ，则它们之间的关系是（）

A、S₁＜S₂＜S₃ B、S₂＜S₁＜S₃ C、S₁＜S₃＜S₂ D、S₃＜S₂＜S₁

查看试题解析
10. 如图，已知在半径为6的⊙O中，点A，B，C在⊙O上且∠ACB＝60°，则 $\overset{⌢}{A B}$ 的长度为（）

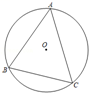A、6π B、4π C、2π D、π

查看试题解析

二、填空题

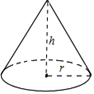
11. 若扇形的圆心角为90°，半径为4，则该扇形的弧长为．

查看试题解析
12. 如图，圆锥的底面半径 $r$ 为 $6 c m$ ，高 $h$ 为 $8 c m$ ，则圆锥的侧面积为．

查看试题解析
13. 圆锥的底面半径为3，侧面积为21π，则这个圆锥的高为．

查看试题解析
14. 如图，点A、B、C、D都在边长为1的网格格点上，以A为圆心，AE为半径画弧，弧EF经过格点D，则扇形AEF的面积是．

查看试题解析
15. 在Rt△ABC中，∠ACB＝90°，AC＝BC＝1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，则图中阴影部分的面积是．

查看试题解析
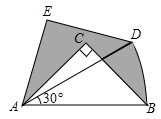16. 已知，如图，扇形AOB中， $∠ A O B = 120 °$ ， $O A = 4$ ，若以点A为圆心，AO长为半径画弧交弧AB于点C，过点C作 $C D ⊥ O A$ ，垂足为点D，则图中阴影部分的面积为.

查看试题解析

三、综合题

17. 如图，在边长为1的正方形组成的网格中建立直角坐标系， $△ A O B$ 的顶点均在格点上，点O为原点，点A、B的坐标分别是 $A (3 ， 2)$ 、 $B (1 ， 3)$ ．

(1)、将 $△ A O B$ 向下平移2个单位后得到 $△ A_{1} O_{1} B_{1}$ ，则点 $B_{1}$ 的坐标为；

(2)、将 $△ A O B$ 绕点O逆时针旋转 $90 °$ 后得到 $△ A_{2} O B_{2}$ ，请在图中作出 $△ A_{2} O B_{2}$ ，并求出这时点 $A_{2}$ 的坐标为 ▲ ；

(3)、在（2）中的旋转过程中，求线段OB扫过的图形的面积．

查看试题解析
18. 如图1所示，在 $△ A B C$ 中， $A B = A C = 12$ ， $∠ C A B = 120 °$ ，P是BC边上一点（不与B、C点重合），将线段AP绕点A逆时针旋转 $120 °$ 得到扇形PAQ．

(1)、求证： $△ A P B ≅ △ A Q C$

(2)、当BC与扇形PAQ相切时，求BQ的长；

(3)、如图2，若 $A P ∥ C Q$ ，求阴影部分的图形的周长．（结果不求近似值）

查看试题解析
19. 如图，在边长为1的正方形组成的网格中建立直角坐标系， $△ A O B$ 的顶点均在格点上，点O为原点，点A ， B的坐标分别是 $A (3 ， 2)$ 、 $B (1 ， 3)$ ．

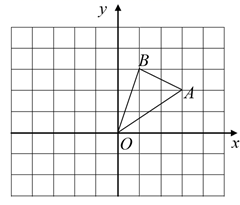(1)、将 $△ A O B$ 向下平移3个单位后得到 $△ A_{1} O_{1} B_{1}$ ，则点 $B_{1}$ 的坐标为；

(2)、将 $△ A O B$ 绕点O逆时针旋转90°后得到 $△ A_{2} O B_{2}$ ，请在图中作出 $△ A_{2} O B_{2}$ ，并求出这时点 $A_{2}$ 的坐标为；

(3)、在（2）中的旋转过程中，求出线段 $O A$ 扫过的图形的弧长．

查看试题解析
20. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连结AC，BC.

(1)、求证：∠A＝∠BCD；

(2)、 $C D = 4 \sqrt{3}$ ，∠B＝60°，求阴影部分的面积.

查看试题解析
21. 将图中的破轮子复原，已知弧上三点A，B，C.

(1)、用尺规作出该轮的圆心O，并保留作图痕迹；

(2)、若半径R＝6，弧BC的度数为120°，则扇形BOC的面积为；（保留π）

(3)、若△ABC是等腰三角形，设底边BC＝8，腰AB＝5，求该轮的半径R.

查看试题解析
22. 在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC＝10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m²）.

(1)、如图1，画出小狗活动的区域，并求出当BC＝2m时S的值.（结果保留π）

(2)、如图2，现考虑在（1）中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，设BC＝x，
①写出面积S与x的关系式；

②在BC的变化过程中，当S取得最小值时，求边BC的长及S的最小值.（结果保留π）

查看试题解析
23. 如图，已知AB是⊙O的直径，点C，D在⊙O上，∠D=60°．

(1)、求∠BAC的度数；

(2)、当BC=4时，求劣弧AC的长．

查看试题解析
24. 如图所示是一个几何体的表面展开图．

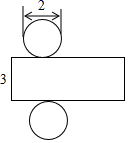(1)、该几何体的名称是，其底面半径为．

(2)、根据图中所给信息，求该几何体的侧面积和体积（结果保留m）

查看试题解析
25. 将一块含有45°的三角板ABC的顶点A放在⊙O上，且AC与⊙O相切于点A（如图1），将△ABC从点A开始，绕着点A顺时针旋转，设旋转角为α（0°＜α＜135°），旋转后，AC、AB分别与⊙O交于点E，F，连接EF（如图2）.已知AC=8，⊙O的半径为4.

(1)、在旋转过程中，有以下几个量：①弦EF的长；② $\overset{⌢}{E F}$ 的长；③∠AFE的度数；④点O到EF的距离.其中不变的量是（填序号）；

(2)、当α＝°时，BC与⊙O相切（直接写出答案）；

(3)、当BC与⊙O相切时，求△AEF的面积.

查看试题解析
26. 如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E.点C是弧BF的中点.

(1)、求证：AD⊥CD；

(2)、若∠CAD=30°.⊙O的半径为3，一只蚂蚁从点B出发，沿着BE--EC--弧CB爬回至点B，求蚂蚁爬过的路程(π≈3.14， $\sqrt{3}$ ≈1.73，结果保留一位小数.)

查看试题解析
27. 如图，在△ABC中，AB＝AC．以BC为直径画圆O分别交AB，AC与点D，E.

(1)、求证：BD＝CE；

(2)、当△ABC中 $∠ B = 70 °$ 且BC＝12时，求 $\overset{⌢}{D E}$ 的长．

查看试题解析
28. 如图，已知AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E，∠D＝65°.

(1)、求∠CAD的度数；

(2)、若AB＝4，求 $\overset{⌢}{B C}$ 的长.

查看试题解析