浙教版备考2022年中考数学一轮复习专题30 直线与圆的位置关系
试卷更新日期:2022-01-10 类型:一轮复习
一、单选题
-
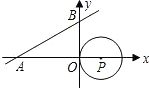
1. ⊙O的半径为6cm,圆心O到直线l的距离为7cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、不能确定2. 如图,直线 与x轴、y 轴分别相交于点A、B两点,圆心P的坐标为(2,0).⊙P与y轴相切于点O,若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是( )
 A、5 B、6 C、7 D、83. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A、5 B、6 C、7 D、83. 如图,在平面直角坐标系中,过边长为1的正方形格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )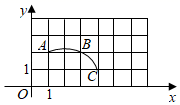 A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)4. 下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )A、1个 B、2个 C、3个 D、0个5. 如图,正三角形 的边长为2,点 , 在⊙O上,点 在⊙O内,⊙O的半径为 ,将正三角形 绕点 逆时针旋转.下列关于嘉嘉和淇淇得出的结论,判断正确的是( )
A、点(5,0) B、点(2,3) C、点(6,1) D、点(1,3)4. 下列命题中:①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③垂直于半径的直线是圆的切线;④E,F是∠AOB的两边OA,OB上的两点,则不同的E,O,F三点确定一个圆:其中正确的有( )A、1个 B、2个 C、3个 D、0个5. 如图,正三角形 的边长为2,点 , 在⊙O上,点 在⊙O内,⊙O的半径为 ,将正三角形 绕点 逆时针旋转.下列关于嘉嘉和淇淇得出的结论,判断正确的是( )嘉嘉:当 第一次与⊙O相切时,旋转角为 ;
淇淇:当点 第一次落在⊙O上时,点 的运动路径长度为 .
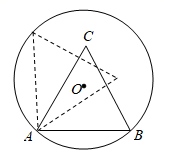 A、只有嘉嘉正确 B、只有淇淇正确 C、两人均正确 D、两人均不正确6. 下列命题中的假命题是( )A、和圆有唯一公共点的直线是圆的切线 B、切线垂直于过切点的半径 C、在同圆或等圆中,等弦所对的圆心角相等 D、平分弦的直径垂直于弦,并且平分弦所对的两条弧7. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )
A、只有嘉嘉正确 B、只有淇淇正确 C、两人均正确 D、两人均不正确6. 下列命题中的假命题是( )A、和圆有唯一公共点的直线是圆的切线 B、切线垂直于过切点的半径 C、在同圆或等圆中,等弦所对的圆心角相等 D、平分弦的直径垂直于弦,并且平分弦所对的两条弧7. 如图,从圆外一点P引圆的两条切线PA,PB,A,B为切点,C为PB上的一点,连接CO交⊙O于点D,若 , , ,则⊙O的半径长是( )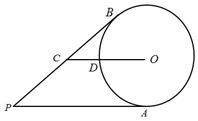 A、 B、 C、4 D、38. 已知PA , PB是⊙O的切线,A , B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )A、63° B、117° C、53°或127° D、117°或63°9. 如图, 和 是 的两条切线, , 为切点,点 在 上,点 , 分别在线段 和 上,且 , .若 ,则 的度数为( )
A、 B、 C、4 D、38. 已知PA , PB是⊙O的切线,A , B是切点,点C是⊙O上不同于点A、点B的一个动点,若∠P=54°,则∠ACB的度数是( )A、63° B、117° C、53°或127° D、117°或63°9. 如图, 和 是 的两条切线, , 为切点,点 在 上,点 , 分别在线段 和 上,且 , .若 ,则 的度数为( )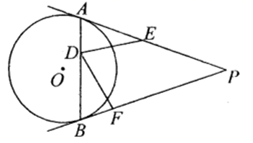 A、 B、 C、 D、10. 如图, 中, ,它的周长为16,若圆O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A、 B、 C、 D、10. 如图, 中, ,它的周长为16,若圆O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )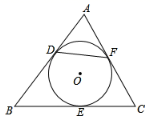 A、2 B、3 C、4 D、6
A、2 B、3 C、4 D、6二、填空题
-
11. 如图,已知 , 分别切⊙O于A、B, 切⊙O于E,若 , ,则△ 周长为.
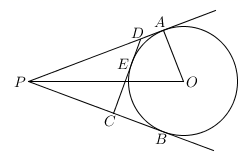 12. 如图,PA、PB是 的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=°.
12. 如图,PA、PB是 的切线,A、B为切点,点C、D在⊙O上.若∠P=102°,则∠A+∠C=°. 13. 如图,等边三角形ABC的边长为4,E、F分别是边AB,BC上的动点,且AE=BF,连接EF,以EF为直径作圆O.当圆O与AC边相切时,AE的长为.
13. 如图,等边三角形ABC的边长为4,E、F分别是边AB,BC上的动点,且AE=BF,连接EF,以EF为直径作圆O.当圆O与AC边相切时,AE的长为.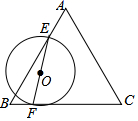 14. 如图,半圆的圆心与坐标原点重合,半圆的半径为2,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是.
14. 如图,半圆的圆心与坐标原点重合,半圆的半径为2,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是.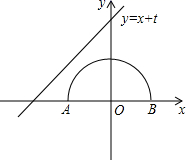 15. 如图1,一个圆球放置在 形架中,图2是它的平面示意图, 和 都是 的切线,切点分别是 ,若 的半径为 ,且 ,则 .
15. 如图1,一个圆球放置在 形架中,图2是它的平面示意图, 和 都是 的切线,切点分别是 ,若 的半径为 ,且 ,则 .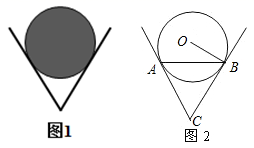 16. 如图,Rt△ABC中,∠ABC=90°,点D是BC边上一点,以BD为直径的半圆与边AC相切于点E.若AB=3,BC=4,则BD=.
16. 如图,Rt△ABC中,∠ABC=90°,点D是BC边上一点,以BD为直径的半圆与边AC相切于点E.若AB=3,BC=4,则BD=.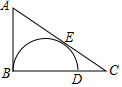
三、综合题
-
17. 如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB CD,BO=6cm.CO=8cm,
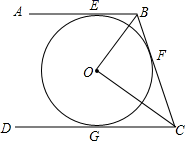 (1)、求证:BO⊥CO;(2)、求⊙O的半径.18. 如图,在 中, ,以 为直径作⊙O交 交于点 ,作切线 交 于点 ,过点 作 ,交 的延长线于点 ,交⊙O于点 ,连接 交 于点 .
(1)、求证:BO⊥CO;(2)、求⊙O的半径.18. 如图,在 中, ,以 为直径作⊙O交 交于点 ,作切线 交 于点 ,过点 作 ,交 的延长线于点 ,交⊙O于点 ,连接 交 于点 .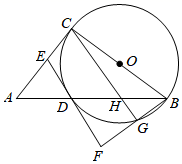 (1)、求证: ;(2)、若 , ,求 的长.19. 已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC于E.
(1)、求证: ;(2)、若 , ,求 的长.19. 已知AB是⊙O的直径,AC是弦,∠BAC的角平分线交⊙O于点D,DE⊥AC于E.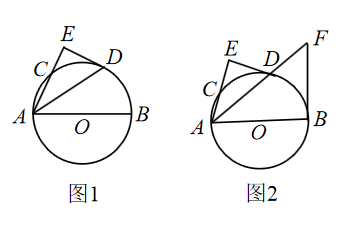 (1)、如图(1)求证:DE是⊙O的切线;(2)、如图(1)若AB=10,AC=6,求ED的长;(3)、如图(2)过点B作⊙O的切线,交AD延长线于F,若ED=DF,求 的值.20. 如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F.
(1)、如图(1)求证:DE是⊙O的切线;(2)、如图(1)若AB=10,AC=6,求ED的长;(3)、如图(2)过点B作⊙O的切线,交AD延长线于F,若ED=DF,求 的值.20. 如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP,AP与OD的延长线交于点P.连接PC并延长与AB的延长线交于点F. (1)、求证:PC是半⊙O的切线;
(1)、求证:PC是半⊙O的切线;
(2)、若∠CAB=30°,AB=10,求由劣弧AC、线段PA和线段PC所围成的图形面积S.
21. 已知:如图,AC⊙O是的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C. (1)、求证:PB是⊙O的切线;(2)、若OP∥BC,且OP=8,BC=2.求⊙O的半径.22. 如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .
(1)、求证:PB是⊙O的切线;(2)、若OP∥BC,且OP=8,BC=2.求⊙O的半径.22. 如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .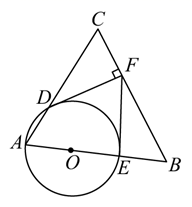 (1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.23. 如图,矩形ABCD中,AB=8,BC=12,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.23. 如图,矩形ABCD中,AB=8,BC=12,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.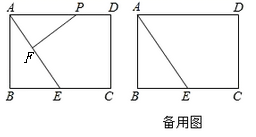 (1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出DP满足的条件:.24. 如图,△ABC是直角三角形,∠ACB=90°.
(1)、求证:△PFA∽△ABE;(2)、当点P在线段AD上运动时,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;(3)、探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出DP满足的条件:.24. 如图,△ABC是直角三角形,∠ACB=90°. (1)、实践与操作利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
(1)、实践与操作利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).①作△ABC的外接圆,圆心为O;
②以线段AC为一边,在AC的右侧作等边△ACD;
③连接BD,交⊙O于点E,连接AE,
(2)、综合与运用 在你所作的图中,若AB=4,BC=2,则:①AD与⊙O的位置关系是.
②线段AE的长为.
25. 已知, 内接于 ,AD、BD为 的弦,且 . (1)、如图1,求证: ;(2)、如图2,过B作 的切线交AC的延长线于E,求证: ;(3)、如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.26. 如图,Rt ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)、如图1,求证: ;(2)、如图2,过B作 的切线交AC的延长线于E,求证: ;(3)、如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.26. 如图,Rt ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.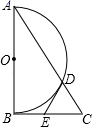 (1)、求证:DE是半圆⊙O的切线.(2)、若∠BAC=30°,DE=2,求AD的长.27. 如图,在 中, , , 的垂直平分线 交 于点O , 以O为圆心, 为半径作 .
(1)、求证:DE是半圆⊙O的切线.(2)、若∠BAC=30°,DE=2,求AD的长.27. 如图,在 中, , , 的垂直平分线 交 于点O , 以O为圆心, 为半径作 .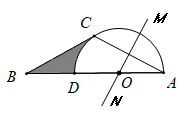 (1)、求证: 是 的切线;(2)、若 的半径为6,求图中阴影部分的面积.28. 如图1所示,在正方形ABCD中,AB=1, 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的任意一点(点E与点A、D不重合),过E作AC所在圆的切线,交边DC于点F,G为切点.
(1)、求证: 是 的切线;(2)、若 的半径为6,求图中阴影部分的面积.28. 如图1所示,在正方形ABCD中,AB=1, 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的任意一点(点E与点A、D不重合),过E作AC所在圆的切线,交边DC于点F,G为切点. (1)、当∠DEF=45°时,求证:点G为线段EF的中点;(2)、设AE=x,FC=y,求y关于x的函数解析式,并写出函数的定义域;(3)、图2所示,将△DEF沿直线EF翻折后得△D1EF,当EF= 时,讨论△AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
(1)、当∠DEF=45°时,求证:点G为线段EF的中点;(2)、设AE=x,FC=y,求y关于x的函数解析式,并写出函数的定义域;(3)、图2所示,将△DEF沿直线EF翻折后得△D1EF,当EF= 时,讨论△AD1D与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.