浙教版备考2022年中考数学一轮复习专题29 圆的基本性质
试卷更新日期：2022-01-09 类型：一轮复习
一、单选题
-
1. 如图，四边形ABCD内接于 ，如果它的一个外角 ，那么 的度数为（ ）
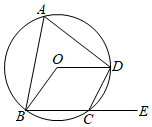A、64° B、128° C、20° D、116°2. 如图，BD是⊙O的直径，点A、C在圆上，且CD＝OB，则∠BAC＝（ ）
A、120° B、90° C、60° D、30°3. 如图，AB是⊙O的直径，CD是⊙O的弦，如果∠ACD=36°，那么∠BAD等于（ ）．
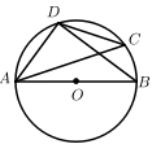A、36° B、44° C、54° D、56°4. 如图， 是半圆 的直径， ， 是 上两点，连接 ， 并延长交于点 ，连接 ， ，如果 ，那么 的度数为（ ）
A、 B、 C、 D、5. 如图，⊙O是△ABC的外接圆，∠OCB＝40°，则∠A的大小为（ ）
A、40° B、50° C、80° D、100°6. 如图所示，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA，OB在O点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE＝8个单位，OF＝6个单位，则圆的直径为（ ）
A、12个单位 B、10个单位 C、1个单位 D、15个单位7. 下列图形中的角是圆周角的是（ ）A、
B、
C、
D、
8. 如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于（ ）
A、20° B、30° C、40° D、50°9. 如图，点A、B、C是⊙O上的三个点，若∠AOB＝82°，则∠C的度数为（ ）
A、82° B、38° C、24° D、41°10. 已知 是半径为6的圆的一条弦，则 的长不可能是（ ）A、8 B、10 C、12 D、14二、填空题
-
11. 如图，在⊙O中，=2 ， AD⊥OC于点D，比较大小AB2AD．（填入“＞”或“＜”或“＝”）．
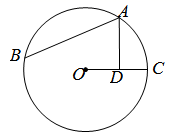12. 如图，四边形ABCD内接于⊙O，且四边形OABC是平行四边形，则∠D＝ ．
13. 在Rt△ABC中，∠C＝90°，AC＝2，BC＝4，如果以点A为圆心，AC为半径作⊙A，那么斜边中点D与⊙A的位置关系是：点D在 ． （填：圆上或圆外或圆内）14. 如图，在⊙O中， =2 ， 于点D，比较大小AB2AD．（填入“＞”或“＜”或“=”）．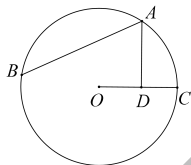
15. 如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是 ．
16. 如图，BD是⊙O的直径，∠CBD＝30°，则∠A的度数为 ．
三、综合题
-
17. 如图，ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
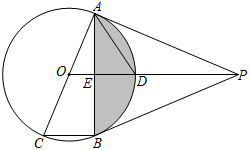
(1)、求证：∠ACD＝∠B；(2)、若BC＝6，AC＝8，求AD、CD的长．18. 如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，点E是BC的中点，连结并延长OE交圆于点D．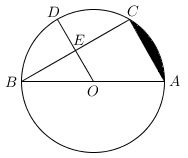
(1)、求证：OD AC．(2)、若DE＝2，BE＝2 ，求阴影部分的面积．19. 如图，BD是圆O的直径，A、C是圆O上的两个点，且AB=AC，AD与BC的延长线交于点E．
(1)、证明： ABD∽ AEB；(2)、若AD=1，DE=3，求圆O的直径的长．20. 如图，AB是 的直径， 于点E，连接CO并延长交AD于点F，且 ．
(1)、求证：E是OB的中点；(2)、若 ，求CD的长．21. 如图，正方形网格中有—段弧，弧上三点 ， ， 均在格点上．
(1)、圆心 的坐标是（）， ．(2)、求 的长度．22. 如图，已知四边形ABCD内接于圆O，连接BD， ， ．
(1)、求证： ；(2)、若圆O的半径为3，求BC的长．23. 如图，在⊙O中， ，CD⊥OA于点D，CE⊥OB于点E．
(1)、求证：CD=CE；(2)、若∠AOB=120°，OA=2，求四边形DOEC的面积．24. 如图，⊙O是四边形ABCD的外接圆，直径BD与弦AC交于点E．若∠BAC＝2∠ABE．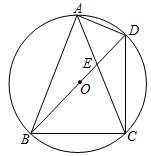
(1)、求证：AB＝AC；(2)、当△BCE是等腰三角形时，求∠BCE的大小；(3)、当AE＝4，CE＝6时，求边BC的长．25. 将图中的破轮子复原，已知弧上三点A，B，C．
(1)、用尺规作出该轮的圆心O，并保留作图痕迹；(2)、若△ABC是等腰三角形，设底边BC＝8，腰AB＝5，求该轮的半径R．26. 如图，△ABC是⊙O的内接三角形，且AB＝AC．
(1)、求证：AO平分∠BAC；(2)、若AB＝ ，BC＝4，求半径OA的长．
