浙教版备考2022年中考数学一轮复习专题26 矩形
试卷更新日期:2022-01-09 类型:一轮复习
一、单选题
-
1. 下列说法中错误的是( )A、两条对角线互相垂直且平分的四边形是菱形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直、平分且相等的四边形是正方形 D、两条对角线互相平分的四边形是平行四边形2. 如图,将矩形纸片 沿 折叠,使点 落在对角线 上的 处.若 ,则 等于( )
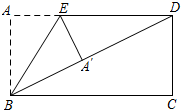 A、 B、 C、 D、3. 下列命题是真命题的是 ( )A、正方形是轴对称图形,但不是中心对称图形 B、对角线互相垂直的平行四边形是矩形 C、四条边相等的四边形是菱形 D、一组对边平行,另一组对边相等的四边形是平行四边形4. 下列说法中错误的是( )A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的平行四边形是菱形 D、两条对角线相等的菱形是正方形5. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ).
A、 B、 C、 D、3. 下列命题是真命题的是 ( )A、正方形是轴对称图形,但不是中心对称图形 B、对角线互相垂直的平行四边形是矩形 C、四条边相等的四边形是菱形 D、一组对边平行,另一组对边相等的四边形是平行四边形4. 下列说法中错误的是( )A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的平行四边形是菱形 D、两条对角线相等的菱形是正方形5. 如图, ,其中 , , ,M为BC中点,EF过点M交AC、BD于点E、F , 连接BE、CF , 则下列结论错误的是( ). A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形6. 如图,在 中, , , , 为边 上一动点, 于 , 于 ,则 的最小值为( )
A、四边形BECF为平行四边形 B、当 时,四边形BECF为矩形 C、当 时,四边形BECF为菱形 D、四边形BECF不可能为正方形6. 如图,在 中, , , , 为边 上一动点, 于 , 于 ,则 的最小值为( ) A、5 B、 C、4 D、37. 如图,有甲、乙、丙三个矩形,其中相似的是( )
A、5 B、 C、4 D、37. 如图,有甲、乙、丙三个矩形,其中相似的是( )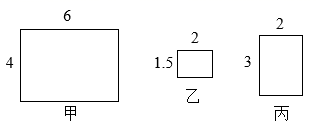 A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似8. 将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.若 , ,则 ( )
A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似8. 将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.若 , ,则 ( ) A、3 B、4 C、 D、9. 如图,在矩形ABCD中,P为BC边的中点,E、F分别为AB、CD边上的点,若BE=2,CF=3,∠EPF=90°,则EF的长为( )
A、3 B、4 C、 D、9. 如图,在矩形ABCD中,P为BC边的中点,E、F分别为AB、CD边上的点,若BE=2,CF=3,∠EPF=90°,则EF的长为( )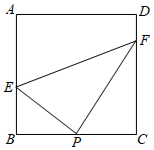 A、5 B、2 C、2 D、410. 如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D , 若点D巧好为线段AB的中点,则AB的长度为( )
A、5 B、2 C、2 D、410. 如图,在Rt△ABC中,∠ACB=90°, AC=3,以点C为圆心、CA为半径的圆与AB交于点D , 若点D巧好为线段AB的中点,则AB的长度为( )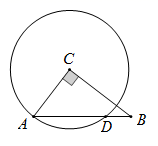 A、 B、3 C、6 D、9
A、 B、3 C、6 D、9二、填空题
-
11. 如图,在矩形ABCD中,AD=8,AB=4,将矩形ABCD折叠,使点A与点C重合,折痕为MN.给出以下四个结论:①△CDM≌△CEN;②△CMN是等边三角形;③CM=5;④BN=3.其中正确的结论序号是 .
 12. 如图所示,在Rt 中, , ,CM是斜边AB上的中线,E、F分别为MB、BC的中点,若 ,则 的面积为 .
12. 如图所示,在Rt 中, , ,CM是斜边AB上的中线,E、F分别为MB、BC的中点,若 ,则 的面积为 . 13. 如图所示,在正方形ABCD中,点P在AC上, , ,垂足分别为E,F, ,则DP的长为 .
13. 如图所示,在正方形ABCD中,点P在AC上, , ,垂足分别为E,F, ,则DP的长为 . 14. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形,BC=8.AE平分∠BAD交BC于点E , 连接OE . 请从A , B两题中任选一题作答(1)、线段AE的长等于 .(2)、线段OE的长等于 .
14. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形,BC=8.AE平分∠BAD交BC于点E , 连接OE . 请从A , B两题中任选一题作答(1)、线段AE的长等于 .(2)、线段OE的长等于 . 15. 如图,矩形 中, , ,连接 .以点 为圆心,以任意长为半径作弧,交 , 分别于点 , :分别以点 , 为圆心,以大于 长为半径作弧,两弧相交于点 :作射线 ,交 于点 .则 的面积为 .
15. 如图,矩形 中, , ,连接 .以点 为圆心,以任意长为半径作弧,交 , 分别于点 , :分别以点 , 为圆心,以大于 长为半径作弧,两弧相交于点 :作射线 ,交 于点 .则 的面积为 . 16. 如图,在矩形ABCD中, ,点E , F分别在BC , CD上,将 沿AE折叠,使点B落在AC上的点 处,又将 沿EF折叠,使点C落在直线 与AD的交点 处, .
16. 如图,在矩形ABCD中, ,点E , F分别在BC , CD上,将 沿AE折叠,使点B落在AC上的点 处,又将 沿EF折叠,使点C落在直线 与AD的交点 处, .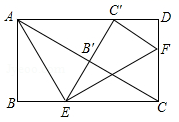
三、综合题
-
17. 如图,将矩形纸片ABCD(AD>DC)的点A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F
 (1)、若BE=1、EC=2,则sin∠EDC=;(2)、若BE:EC=1:4,CD=9,求BF的长;(3)、若BE:EC=m:n,求AF:FB(用含有m、n的代数式表示)18. 如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.
(1)、若BE=1、EC=2,则sin∠EDC=;(2)、若BE:EC=1:4,CD=9,求BF的长;(3)、若BE:EC=m:n,求AF:FB(用含有m、n的代数式表示)18. 如图,将矩形纸片ABCD(AD>DC)的∠A沿着过点D的直线折叠,使点A落在BC边上,落点为E,折痕交AB边于点F.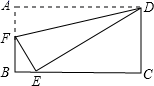 (1)、图中的全等三角形是 , 相似三角形是 .(2)、若BE:EC=1:4,CD=9,求BF的长;(3)、若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)19. 如图,菱形 的对角线 , 相交于点 , 是 的中点,点 、 在 上, , .
(1)、图中的全等三角形是 , 相似三角形是 .(2)、若BE:EC=1:4,CD=9,求BF的长;(3)、若BE:EC=m:n,求AF:FB.(用含有m,n的代数式表示)19. 如图,菱形 的对角线 , 相交于点 , 是 的中点,点 、 在 上, , .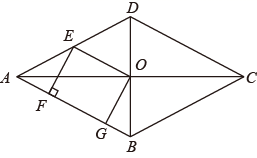 (1)、求证:四边形 是矩形;(2)、若 , ,求 和 的长.20. 如图,在正方形 中,点 在对角线 上(不与点 ,点 重合), 于点 , 于点 ,连结 ,
(1)、求证:四边形 是矩形;(2)、若 , ,求 和 的长.20. 如图,在正方形 中,点 在对角线 上(不与点 ,点 重合), 于点 , 于点 ,连结 , (1)、写出线段 , , 长度之间的数量关系,并说明理由.(2)、若正方形 的边长为 , ,求线段 的长.21. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)、写出线段 , , 长度之间的数量关系,并说明理由.(2)、若正方形 的边长为 , ,求线段 的长.21. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF. (1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.22. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2.
(1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.22. 如图,小亮父亲想用长80m的栅栏.再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长50m,设矩形ABCD的边AB=xm,面积为Sm2. (1)、写出S与x之间的函数表达式,并写出x的取值范围.(2)、当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?23. 如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF.
(1)、写出S与x之间的函数表达式,并写出x的取值范围.(2)、当AB,BC分别为多少米时,羊圈的面积最大?最大值是多少?23. 如图,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,点E是边BC延长线上一点,连接AE、DE,过点C作CF⊥DE于点F,且DF=EF. (1)、求证:AD=CE.(2)、若CD=5,AC=6,求△AEB的面积.24. 定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
(1)、求证:AD=CE.(2)、若CD=5,AC=6,求△AEB的面积.24. 定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
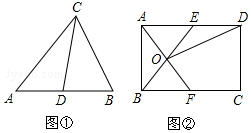 (1)、求证:△AOB和△AOE是“友好三角形”;(2)、连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.25. 如图1,在Rt 中, ,AC=BC=4,D是AB的中点.延长 至点 ,在 右侧作 ,点 为射线 上一点,连结 交 于点 ,过点 作 交 于点 .
(1)、求证:△AOB和△AOE是“友好三角形”;(2)、连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.25. 如图1,在Rt 中, ,AC=BC=4,D是AB的中点.延长 至点 ,在 右侧作 ,点 为射线 上一点,连结 交 于点 ,过点 作 交 于点 . (1)、求证: ;(2)、如图 2,点 在射线 上,且 平分 ,连结 .
(1)、求证: ;(2)、如图 2,点 在射线 上,且 平分 ,连结 .①求证: ;
②当 是以 为腰的等腰三角形时,则 .(直接写出答案,结果保留根号).
26. 如图,矩形 中, , , 为 上一点,将 沿 翻折至 , 与 相交于点 , 与 相交于点F,且 . (1)、求证: ;(2)、若设 为 ,试求 (用含 的代数式表示);(3)、求 的长.
(1)、求证: ;(2)、若设 为 ,试求 (用含 的代数式表示);(3)、求 的长.