浙教版备考2022年中考数学一轮复习专题24 直角三角形
试卷更新日期：2022-01-09 类型：一轮复习
一、单选题
-
1. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．连结AE，若大正方形ABCD的面积为169，△ABE的面积为72，则小正方形EFGH的面积是（ ）
A、36 B、49 C、48 D、502. 如图，圆柱的底面周长是14cm，圆柱高为24cm，一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B，那么它爬行的最短路程为（ ）
A、14cm B、15cm C、24cm D、25cm3. 已知a、b、c是三角形的三边长，如果满足（a﹣3）2 +|c﹣5|＝0，则三角形的形状是（ ）A、等腰三角形 B、直角三角形 C、锐角三角形 D、钝角三角形4. 四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”（如图），其直角三角形的两条直角边长分别为2和3，则小正方形与大正方形的面积比是（ ）
A、1：13 B、1：14 C、2：9 D、2：155. 已知直角三角形的两条直角边的长是方程x2﹣7x+12＝0的两根，则这个直角三角形外接圆的半径（ ）A、7 B、2.5 C、 D、56. 如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置，若四边形AECF的面积为25，DE=2，则AE的长为（ ）
A、5 B、 C、7 D、7. Rt△ABC中，∠C=90°，AC=2，BC=4，如果以点为圆心，AC为半径作⊙A，那么斜边AB的中点D与⊙A的位置关系是（ ）．A、点D在⊙A外 B、点D在⊙A上 C、点D在⊙A内 D、无法确定8. 如图，PA、PB分别切⊙O于A，B，∠APB=60°，⊙O半径为2，则PB的长为（ ）．
A、3 B、4 C、 D、9. 如图，在 ABC中，∠ABC的平分线BP与AC的垂直平分线DP相交于点P ， 过点P作PF⊥BC于点F ， PE⊥AB交BA的延长线于点E ． AB=7cm，BC=15cm，则AE的长为（ ）
A、3cm B、4cm C、5cm D、6cm10. 一个长方形抽屉长 ，宽 ，贴抽屉底面放一根木棒，那么这根木棒最长（不计木棒粗细）可以是（ ）A、 B、 C、 D、二、填空题
-
11. 已知一个直角三角形两条直角边的长分别是a和3，则斜边长是；已知一个圆的面积为S，则该圆的半径是12. 如图，在等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB，且∠EBD =∠CBD，连接DE、CE，则下列结论； ①∠DAC=∠DBC；②BE⊥AC； ③∠DEB=30°.
④若EC//AD，则S△EBC=1.其中正确的有 ． （只填序号）
13. 如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是 ．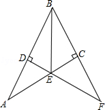
14. 如图，在等边三角形ABC中，CD⊥AB于点D，若AB=2，则CD的长是 ．
15. 某校八年级数学兴趣小组活动，准备将一块底为10cm，高为12.8cm的三角形纸板分割成四块(如图1)，然后将这四块拼成一张正方形纸板(无缝隙不重叠，如图2)，则DG 的长是cm，CF的长是cm．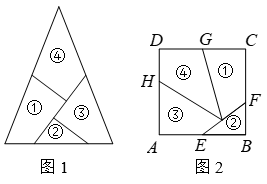
16. 如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F点处，已知DE＝5，AB＝8，则BF＝ ．
17. 如图所示的圆柱体中底面圆的周长是2，高为3，若一只小虫从A点出发沿着圆柱体的侧面匀速爬行一周到B点，则小虫爬行的最短路程是 ．
三、综合题
-
18. 如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按逆时针旋转得到△ADC，连接OD，OA．
(1)、求∠ODC的度数；(2)、若OB=2，OC=3，求AO的长．19. 已知一个直角三角形的斜边长为41，一条直角边长为x．(1)、用关于x的代数式表示这个直角三角形的另一条直角边长；(2)、当x=40时，求另一条直角边的长．20. 如图，在平面直角坐标系中，点A(-4，0)，C(3，0)，D(0，4)， AG⊥CD于点G，交y轴于点B.
(1)、求证：△AOB≌△DOC．(2)、点E在线段AB上，作OF⊥OE交CD于点F，连结EF．①若E是AB的中点，求△OEF的面积.
②连结DE，当△DEF是以DE为腰的等腰三角形时，求CF的长．
21. 如图，在△ABC中，AB=AC，CD⊥AB于点D，过点D作DE⊥BC于点E，交CA的延长线于点F．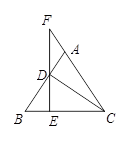
(1)、求证：△ADF是等腰三角形．(2)、当CD 8，CF=10时，求BD的长．22. 如图，在△ABC中，∠ACB＝90°，AC＝3，BC＝4．点P从点A出发，在线段AB上以每秒1个单位长度的速度向终点B运动，连接CP．设点P运动的时间为t秒．
(1)、填空：AB＝；(2)、当t为何值时，CP平分∠ACB；(3)、当t为何值时，△BCP为等腰三角形．23. 如图，△ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．
(1)、求证：∠ACD= ∠B；(2)、若BC＝6，AC＝8，求AD和CD的长．24. 如图，点O是等边三角形ABC内部一点，且满足∠BOC=150°，将△BOC绕点C按顺时针旋转至△ADC的位置，连接OD，OA．
(1)、求∠ODC的度数；(2)、若OB=2，OC=3，求AO的长.25. 在平面直角坐标系中，长方形OABC的边OA在x轴上，OC在y轴上，B（4，3），点M从点A开始，以每秒1个单位长度的速度沿AB→BC→CO运动，设△AOM的面积为S ， 点M运动的时间为t ．
(1)、当0＜t＜3时，AM=；当7＜t＜10时，OM= ． （用含t的代数式表示）(2)、当7＜t＜10时，求S关于t的函数关系式；(3)、当t=8时，在x轴上是否存在一点H ， 使得△MBH是以MB为直角边的直角三角形，若存在，请求出点H的坐标；若不存在，请说明理由．26. 已知：如图1，OA＝2，∠A＝90°， ，OB平分∠AOC ， 且CB⊥OB于点B ．
(1)、求OC的长；(2)、将图1的四边形ABCO折叠，如图2，使点C与点A重合，折痕为FG ， 求OG的长．27. 如图，C为线段BD上一动点，分别过点B、D作 ， ，连接AC、EC ． 已知 ， ， ，设 ．
(1)、用含x的代数式表示 的长．(2)、请问点C满足什么条件时， 的值最小，并求出此时 的最小值．(3)、根据（2）中的规律和结论，重新构图求出代数式 的最小值．28. 如图， ， ， ， ，垂足分别为 ， ．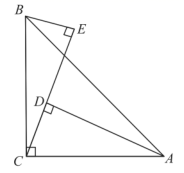
(1)、求证： ；(2)、若 ， ，请直接写出 的长．
