浙教版备考2022年中考数学一轮复习专题21 三角形与全等三角形
试卷更新日期:2022-01-09 类型:一轮复习
一、单选题
-
1. 若一个三角形的三边长为a,b,c,且满足a2-2ab+b2+ac-bc =0,则这个三角形是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形2. 如图所示,已知点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以是( )
 A、∠E=∠C B、 AC∥EF C、∠ABC=∠FDE D、 AB=DF3. 如图, △ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:
A、∠E=∠C B、 AC∥EF C、∠ABC=∠FDE D、 AB=DF3. 如图, △ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F; ②2∠DAE=∠ABD-∠ACE; ③S△AEB:S△AEC=AB:AC; ④∠AGH=∠BAE+∠ACB.
其中正确的结论有( )个.
 A、1 B、2 C、3 D、44. 在等腰△ABC中,AB=AC,其周长为24cm,则AB边的取值范围是( )A、1cm<AB<12cm B、6cm<AB<8cm C、6cm<AB<12cm D、8cm<AB<12cm5. 若一个等腰三角形的两边m,n满足9m2-n2=-13,3m+n=13,则该等腰三角形的周长为( )A、11 B、13 C、16 D、11或166. 如图,在△ABC和△BAD中,已知∠CAB=∠DBA,添加下列条件,还不一定能判定△ABC≌△BAD的是( )
A、1 B、2 C、3 D、44. 在等腰△ABC中,AB=AC,其周长为24cm,则AB边的取值范围是( )A、1cm<AB<12cm B、6cm<AB<8cm C、6cm<AB<12cm D、8cm<AB<12cm5. 若一个等腰三角形的两边m,n满足9m2-n2=-13,3m+n=13,则该等腰三角形的周长为( )A、11 B、13 C、16 D、11或166. 如图,在△ABC和△BAD中,已知∠CAB=∠DBA,添加下列条件,还不一定能判定△ABC≌△BAD的是( ) A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM7. 下列长度的三条线段,能首尾相连围成三角形的是( )A、1cm,2cm,3cm B、2cm,3cm,4cm C、1cm,1cm,2cm D、1cm,2cm,4cm8. 如图,圆柱的底面周长是14cm,圆柱高为24cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为( )
A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM7. 下列长度的三条线段,能首尾相连围成三角形的是( )A、1cm,2cm,3cm B、2cm,3cm,4cm C、1cm,1cm,2cm D、1cm,2cm,4cm8. 如图,圆柱的底面周长是14cm,圆柱高为24cm,一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B,那么它爬行的最短路程为( ) A、14cm B、15cm C、24cm D、25cm9. 如图, ,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若 ,则 的大小为( )度.
A、14cm B、15cm C、24cm D、25cm9. 如图, ,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若 ,则 的大小为( )度. A、8 B、16 C、32 D、6410. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D为AC上任一点,F为AB中点,连接BD,E在BD上,且满足CD2=DE•BD,连接EF,则EF的最小值为( )
A、8 B、16 C、32 D、6410. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,D为AC上任一点,F为AB中点,连接BD,E在BD上,且满足CD2=DE•BD,连接EF,则EF的最小值为( ) A、 ﹣1 B、1 C、 D、
A、 ﹣1 B、1 C、 D、二、填空题
-
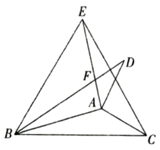
11. 如图,在等边△ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD =∠CBD,连接DE、CE,则下列结论; ①∠DAC=∠DBC;②BE⊥AC; ③∠DEB=30°.
④若EC//AD,则S△EBC=1.其中正确的有 . (只填序号)
 12. 如图,△ABC中,∠A=60°将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′DB=50°,那么∠A′ED的度数为 .
12. 如图,△ABC中,∠A=60°将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′DB=50°,那么∠A′ED的度数为 .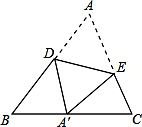 13. 有一个三角形纸片 , ,点D是 边上一点,沿 方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则 的度数可以是 .
13. 有一个三角形纸片 , ,点D是 边上一点,沿 方向剪开三角形纸片后,发现所得的两纸片均为等腰三角形,则 的度数可以是 . 14. 如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是 .
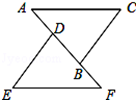
14. 如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=2,△ABC的面积是 . 15. 如图,已知 与 相交于点E, ,点E为 的中点,点D是 上一点,如果 , .求 的长.
15. 如图,已知 与 相交于点E, ,点E为 的中点,点D是 上一点,如果 , .求 的长. 16. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是.
16. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是.
三、综合题
-
17. 如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
 (1)、观察猜想:图1中,线段PF与PG的数量关系是 , ∠FPG=(用含α的代数式表示)(2)、探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.18. 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,
(1)、观察猜想:图1中,线段PF与PG的数量关系是 , ∠FPG=(用含α的代数式表示)(2)、探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.18. 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
 (1)、求证:△BCD≌△ACE.(2)、当CD AB时,求证:AB=2CE.19. 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)、求证:△BCD≌△ACE.(2)、当CD AB时,求证:AB=2CE.19. 如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F. (1)、若△CMN的周长为25cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数 .20. 如图,在平面直角坐标系中,点A( 1, 2) ,B(5, 2) .点C(2a +1,2 a) 在第一象限内,过点C作直线CD∥AB,交y轴于点D.
(1)、若△CMN的周长为25cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数 .20. 如图,在平面直角坐标系中,点A( 1, 2) ,B(5, 2) .点C(2a +1,2 a) 在第一象限内,过点C作直线CD∥AB,交y轴于点D. (1)、若AB= CD,求点C的坐标.(2)、若△ABC的面积为9,求△ABC的周长.21. 如图,在平面直角坐标系中,点A(-4,0),C(3,0),D(0,4), AG⊥CD于点G,交y轴于点B.
(1)、若AB= CD,求点C的坐标.(2)、若△ABC的面积为9,求△ABC的周长.21. 如图,在平面直角坐标系中,点A(-4,0),C(3,0),D(0,4), AG⊥CD于点G,交y轴于点B. (1)、求证:△AOB≌△DOC.(2)、点E在线段AB上,作OF⊥OE交CD于点F,连结EF.
(1)、求证:△AOB≌△DOC.(2)、点E在线段AB上,作OF⊥OE交CD于点F,连结EF.①若E是AB的中点,求△OEF的面积.
②连结DE,当△DEF是以DE为腰的等腰三角形时,求CF的长.
22. 如图, , , , .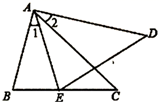 (1)、试说明: ;(2)、求 的度数.23. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.点P从点A出发,在线段AB上以每秒1个单位长度的速度向终点B运动,连接CP.设点P运动的时间为t秒.
(1)、试说明: ;(2)、求 的度数.23. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4.点P从点A出发,在线段AB上以每秒1个单位长度的速度向终点B运动,连接CP.设点P运动的时间为t秒. (1)、填空:AB=;(2)、当t为何值时,CP平分∠ACB;(3)、当t为何值时,△BCP为等腰三角形.24. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.动点P从点A出发,沿AB以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作PD⊥AC于点D,以AP,AD为边作▱APED.设点P的运动时间为t秒.
(1)、填空:AB=;(2)、当t为何值时,CP平分∠ACB;(3)、当t为何值时,△BCP为等腰三角形.24. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.动点P从点A出发,沿AB以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作PD⊥AC于点D,以AP,AD为边作▱APED.设点P的运动时间为t秒. (1)、线段AD的长为(用含t的代数式表示).(2)、当点E落在BC边上时,求t的值.(3)、连结BE,当tan∠CBE= 时,求t的值.(4)、若线段PE的中点为Q,当点Q落在△ABC一边垂直平分线上时,直接写出t的值.25. 如图,在 ABC中,AB=AC , ∠BAC=90°,点A在直线l上,BM⊥,CN⊥l , 垂足分别为M , N .
(1)、线段AD的长为(用含t的代数式表示).(2)、当点E落在BC边上时,求t的值.(3)、连结BE,当tan∠CBE= 时,求t的值.(4)、若线段PE的中点为Q,当点Q落在△ABC一边垂直平分线上时,直接写出t的值.25. 如图,在 ABC中,AB=AC , ∠BAC=90°,点A在直线l上,BM⊥,CN⊥l , 垂足分别为M , N . (1)、你能找到一对全等的三角形吗?并说明理由.(2)、线段BM , CN , MN之间有何数量关系?并说明理由.26. 定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB , OC=OD , ∠AOB=∠COD .
(1)、你能找到一对全等的三角形吗?并说明理由.(2)、线段BM , CN , MN之间有何数量关系?并说明理由.26. 定义:顶角相等且顶点重合的两个等腰三角形叫做对顶三角形.如图1,在 OAB与 OCD中,OA=OB , OC=OD , ∠AOB=∠COD . (1)、如图1, OAB与 OCD是对顶三角形,且A , O , C三点共线请判断AB与CD的位置关系,并说明理由.(2)、如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC , BD , 试探究线段AC , BD之间的关系,并说明理由.(3)、如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD , BC , 取AD的中点E , 连接EO并延长交BC于点F , 延长OE至点G , 使EG=OE , 连接AG , 求证:EF⊥BC .27. 如图,在等腰 ABC中,AB=AC=6cm,∠B=30°,点D在BC边上由点C向点B匀速运动(点D不与点B , C重合),速度为2cm/s,连接AD , 作∠ADE=30°,DE交线段AC于点E .
(1)、如图1, OAB与 OCD是对顶三角形,且A , O , C三点共线请判断AB与CD的位置关系,并说明理由.(2)、如图2, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AC , BD , 试探究线段AC , BD之间的关系,并说明理由.(3)、如图3, OAB与 OCD是对顶三角形,∠AOB=∠COD=90°,连接AD , BC , 取AD的中点E , 连接EO并延长交BC于点F , 延长OE至点G , 使EG=OE , 连接AG , 求证:EF⊥BC .27. 如图,在等腰 ABC中,AB=AC=6cm,∠B=30°,点D在BC边上由点C向点B匀速运动(点D不与点B , C重合),速度为2cm/s,连接AD , 作∠ADE=30°,DE交线段AC于点E . (1)、在此运动过程中,∠BDA逐渐变(填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD=°.(2)、点D运动3s后到达图2位置,则CD=cm.此时 ABD和 DCE是否全等,请说明理由.(3)、在点D运动过程中, ADE的形状也在变化.当 ADE是等腰三角形时,∠BDA的度数为 .
(1)、在此运动过程中,∠BDA逐渐变(填“大”或“小”);D点运动到图1位置时,∠BDA=75°,则∠BAD=°.(2)、点D运动3s后到达图2位置,则CD=cm.此时 ABD和 DCE是否全等,请说明理由.(3)、在点D运动过程中, ADE的形状也在变化.当 ADE是等腰三角形时,∠BDA的度数为 .