浙教版备考2022年中考数学一轮复习专题15 反比例函数的图象与性质

试卷更新日期：2022-01-09 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知一次函数y₁=kx-b 与反比例函数y₂= $\frac{k}{x}$ ，在同一平面直角坐标系中的图象如图所示，则当kx< $\frac{k}{x}$ +b时，x的取值范围是（）

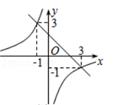A、x<-1或0<x<3 B、-1<x<0或x>3 C、-3<x<0或x> 1 D、x>3

查看试题解析
2. 下列各问题中，两个变量之间的关系不是反比例函数的是

A、小明完成100m赛跑时，时间t（s）与跑步的平均速度v（m/s）之间的关系. B、菱形的面积为48cm² ，它的两条对角线的长为y（cm）与x（cm）的关系. C、一个玻璃容器的体积为30L时，所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时，压强p与受力面积S之间的关系.

查看试题解析
3. 两个反比例函数 $y = \frac{k}{x}$ 和 $y = \frac{1}{x}$ 在第一象限内的图象如图所示，点P在 $y = \frac{k}{x}$ 的图象上， $P C ⊥ x$ 轴于点C，交 $y = \frac{1}{x}$ 的图象于点A， $P D ⊥ y$ 轴于点D，交 $y = \frac{1}{x}$ 的图象于点B，当点P在 $y = \frac{k}{x}$ 的图象上运动时，下列结论错误的是（）

A、 $△ O D B$ 与 $△ O C A$ 的面积相等 B、当点A是PC的中点时，点B一定是PD的中点 C、 $\frac{C A}{P A} = \frac{D B}{P B}$ D、只有当四边形OCPD为正方形时，四边形PAOB的面积最大

查看试题解析
4. 下列各点中，在反比例函数y＝﹣ $\frac{4}{x}$ 图象上的是（）

A、（﹣1，4） B、（1，4） C、（﹣2，﹣2） D、（2，2）

查看试题解析
5. 二次函数y＝ax²＋bx＋c（abc≠0）的图象如图所示，反比例函数y＝ $\frac{c}{x}$ 与正比例函数y＝bx在同一坐标系内的大致图象是（）

A、 B、 C、 D、

查看试题解析
6. 设 $A ， B ， C ， D$ 是反比例函数 $y = \frac{1}{x}$ 图象上的任意四点，现有以下结论：
①存在无数个四边形 $A B C D$ 是平行四边形； ②存在无数个四边形 $A B C D$ 是菱形；

③存在无数个四边形 $A B C D$ 是矩形； ④至少存在一个四边形 $A B C D$ 是正方形.

其中正确结论的个数是（）

A、 $3$ B、 $2$ C、 $1$ D、 $0$

查看试题解析
7. 函数y＝ $\frac{- a^{2} - 1}{x}$ （a为常数）的图象上有三点（x₁ ， ﹣4），（x₂ ， 1），（x₃ ， 3），则x₁ ， x₂ ， x₃的大小关系是（）

A、x₁＜x₂＜x₃ B、x₂＜x₃＜x₁ C、x₃＜x₂＜x₁ D、x₃＜x₁＜x₂

查看试题解析
8. 已知点（x₁ ， y₁）和（x₂ ， y₂）都在反比例函数y＝﹣ $\frac{3}{x}$ 的图象上，如果x₁＜x₂ ，那么y₁与y₂的大小关系正确的是（　　）

A、y₁＜y₂ B、y₁＝y₂ C、y₁＞y₂ D、无法判断

查看试题解析
9. 如图，在平面直角坐标系中，一条直线与反比例函数y= $\frac{4}{x}$ （x＞0）的图象交于两点A、B ，与x轴交于点C ，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y= $\frac{1}{x}$ （x＞0）的图象交于两点D、E ，连接DE ，则四边形ABED的面积为（　　）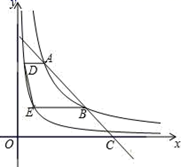

A、4 B、 $\frac{9}{4}$ C、 $\frac{9}{2}$ D、 $\frac{11}{2}$

查看试题解析
10. 函数 $y = a x$ 与 $y = \frac{b}{x} (a b \neq 0)$ 的图象的两个交点的坐标分别为 $(3 ， m)$ ， $(n ， - 2)$ ，则 $m$ ， $n$ 的值分别是（）

A、2，﹣3 B、﹣2，﹣3 C、﹣2，3 D、2，3

查看试题解析

二、填空题

11. 如图，已知一次函数y＝ax（a＜0）与反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象相交于点A，过点A作AB⊥y轴，垂足为B，若△OAB的面积为4，则k的值为．

查看试题解析
12. 如图，已知A₁ ， A₂ ， A₃ ， …，A_n是x轴上的点，且OA₁＝A₁A₂＝A₂A₃＝…＝A_n_－1A_n＝1，分别过点A₁ ， A₂ ， A₃ ， …，A_n作x轴的垂线交二次函数y＝ $\frac{1}{2}$ x²(x＞0)的图象于点P₁ ， P₂ ， P₃ ， …，P_n ，若记△OA₁P₁的面积为S₁ ，过点P₁作P₁B₁⊥A₂P₂于点B₁ ，记△P₁B₁P₂的面积为S₂ ，过点P₂作P₂B₂⊥A₃P₃于点B₂ ，记△P₂B₂P₃的面积为S₃……依次进行下去，则S₃＝，最后记△P_n_－1B_n_－1P_n(n＞1)的面积为S_n ，则S_n＝．

查看试题解析
13. 如图，矩形△ABC的两边OA、OC分别在x轴和y轴上，以AC为边作平行四边形ACDE，E点在CB的延长线上，反比例函数y= $\frac{k}{x}$ (x>0)过B点且与CD交于F点，CF=3DF，S_△ABF=6，则k的值为

查看试题解析
14. 如图，矩形 $A B C D$ 的顶点 $D$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，且点 $D$ 在第一象限，顶点 $B ， C$ 在 $x$ 轴上，对角线 $A C$ 的延长线交 $y$ 轴于点 $E$ ，若 $△ B C E$ 的面积是 $12$ ，则 $k =$ .

查看试题解析
15. 如图，一次函数为y₁＝kx+b（k≠0）的图象与反比例函数y₂＝ $\frac{m}{x}$ （m≠0）的图象交于A（1，t+1），B（t﹣5，﹣1）两点，当y₁＞y₂时，自变量x的取值范围为．

查看试题解析
16. 在平面直角坐标系中，点A（﹣4，1）为直线y＝kx（k≠0）和双曲线y＝ $\frac{m}{x}$ （m≠0）的一个交点，点B（﹣5，0），如果在直线y＝kx上有一点P ，使得S_△ABP＝2S_△ABO ，那么点P的坐标是．

查看试题解析

三、综合题

17. 如图，在平面直角坐标系中，一次函数y＝ax＋b（a≠0）的图象分别交x轴，y轴于A，B两点，与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象交于C，D两点，DE⊥轴于点E，点C的坐标为（6，﹣1），DE＝3

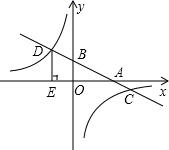(1)、求反比例函数与一次函数的表达式；

(2)、求△COD的面积．

查看试题解析
18. 已知反比例函数y＝ $\frac{2 - k}{x}$ 的图象经过点A（3，﹣2）．

(1)、求k的值．

(2)、点C（x₁ ， y₁），B（x₂ ， y₂）均在反比例函数y＝ $\frac{2 - k}{x}$ 的图象上，若0＜x₁＜x₂ ，直接写出y₁ ， y₂的大小关系．

查看试题解析
19. 如图，在平面直角坐标系中，矩形ABCD的对角线AC的中点与坐标原点重合，点E是x轴上一点，连接AE、BE，若AD平分∠OAE，反比例函数y＝ $\frac{k}{x}$ （k＜0，x＜0）的图象经过AE上的点A、F，且AF＝EF，△ABE的面积为18。

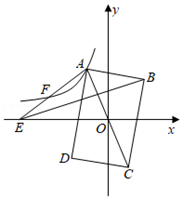(1)、连接BD，证明AF∥BD.

(2)、连接OF，求△AOF的面积.

(3)、求k的值.

查看试题解析
20. 如图，正比例函数y＝ $\frac{1}{2}$ x的图像与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图像交于A（a ， ﹣2）、B两点．

(1)、求反比例函数的解析式和点B的坐标．

(2)、点P为第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C ，连接PO ，如果△POC的面积为3，求点P的坐标．

查看试题解析
21. 在平面直角坐标系xOy中，点A（m ， 6），B（n ， 1）在反比例函数y＝ $\frac{k}{x}$ （k≠0）的第一象限内的图像上．过点A向x轴作垂线，垂足为C；过点B向x轴作垂线，垂足为D ，且CD＝5．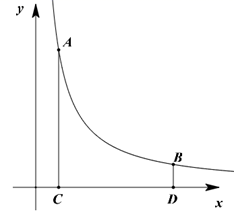

(1)、求m ， n的值，并求出反比例函数的解析式；

(2)、联结AB、AO、BO ，求S_△OAB ．

查看试题解析
22. 如图，一次函数 $y = a x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象交于第一象限C ， D两点，坐标轴交于A、B两点，连结OC ， OD（O是坐标原点）．

(1)、利用图中条件，求反比例函数的解析式和m的值；

(2)、求△DOC的面积．

(3)、双曲线上是否存在一点P ，使得△POC和△POD全等？若存在，给出证明并求出点P的坐标；若不存在，说明理由．

查看试题解析
23. 如图，一次函数y＝ $\frac{1}{2}$ x＋1的图象与轴交于点A ，与y轴交于点C ，与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象交于B ， D两点，且AC＝BC ．

(1)、写出点A ， B的坐标；

(2)、求出点D的坐标，并直接写出当 $\frac{k}{x}$ ＞ $\frac{1}{2}$ x＋1时，x的取值范围；

(3)、若P是x轴上一点，PM⊥x轴交一次函数于点M ，交反比例函数于点N ，当O ， C ， M ， N为顶点的四边形为平行四边形时，请直接写出点P的坐标．

查看试题解析
24. 泡茶需要将电热水壶中的水先烧到100℃，然后停止烧水，等水温降低到适合的温度时再泡茶，烧水时水温y(℃)与时间x(min)成一次函数关系；停止加热过了1分钟后，水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图)．已知水壶中水的初始温度是20℃，降温过程中水温不低于20℃．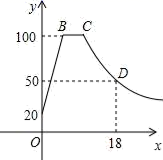

(1)、分别求出图中所对应的函数关系式，并且写出自变量x的取值范围：

(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶，问从水烧开到泡茶需要等待多长时间？

查看试题解析
25. 如图，已知反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点A（4，2），过A作AC⊥y轴于点C ．点B为反比例函数图象上的一动点，过点B作BD⊥x轴于点D ，连接AD ．直线BC与x轴的负半轴交于点E ．

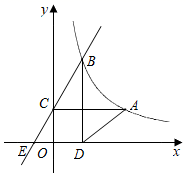(1)、求k的值；

(2)、连接CD ，求△ACD的面积；

(3)、若BD＝3OC ，求四边形ACED的面积．

查看试题解析
26. 用洗衣粉洗衣物时，漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.某天，小金、小东放学回家后各自洗一件完全相同的衣服，漂洗时，小金每次用水约6升，小东每次用水约5升，他们都用了5克洗衣粉，第一次漂洗后，小金的衣服残留的洗衣粉还有1.5克，小东的衣服残留的洗衣粉还有2克.

(1)、分别求出小金、小东衣服漂洗后洗衣粉残留量 $y$ 关于次数 $x$ 的函数解析式.

(2)、已知洗衣粉的残留量降至0.35克时，便视为衣服漂洗干净，若以把衣服洗干净为前提，节约用水为目标，判断小金和小东两种漂洗方法用水量的大小，并说明理由.

查看试题解析
27. 如图，矩形 $O A B C$ 的顶点A，C分别落在x轴，y轴的正半轴上，顶点 $B (2 ， 2 \sqrt{3})$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与 $B C$ ， $A B$ 分别交于D，E， $B D = \frac{1}{2}$ ．

(1)、求反比例函数关系式和点E的坐标；

(2)、写出 $D E$ 与 $A C$ 的位置关系并说明理由；

(3)、点F在直线 $A C$ 上，点G是坐标系内点，当四边形 $B C F G$ 为菱形时，求出点G的坐标．

查看试题解析
28. 如图，在平面直角坐标系中，一次函数y＝ax＋b（a≠0）的图象与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象交于第一、三象限的A、B两点，与x轴交于点C、与y轴交于点D，OC＝1、BC＝5， sin∠BCO＝ $\frac{3}{5}$ ．

(1)、求反比例函数与一次函数的表达式．

(2)、在y轴上有一点E（O点除外），使得S_△BDE＝3S_△BDO ，求点E的坐标．

(3)、根据图像直接回答：当x为何值时，一次函数的值大于反比例函数的值．

查看试题解析