浙教版备考2022年中考数学一轮复习专题5 二次根式

试卷更新日期：2022-01-08 类型：一轮复习

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a}$ (a≥0)是（）

A、正数 B、负数 C、0 D、非负数

查看试题解析
2. 若二次根式 $\sqrt{3 n}$ 的值是整数，则下列n的取值不符合条件的是（）

A、n=3 B、n=12 C、n=18 D、n=27

查看试题解析
3. 若二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（）

A、x<2 B、x≠2 C、x≤2 D、x≥2

查看试题解析
4. 下列各式中，不是二次根式的是（）

A、 $\sqrt{45}$ B、 $\sqrt{- 3}$ C、 $\sqrt{（ a + 3)^{2}}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
5. 下列各式中，正确的是（　　）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$ B、 $\sqrt{27} \div \sqrt{3} = 9$ C、 $(\sqrt{5} + 1) (\sqrt{5} - 1) = 4$ D、 ${(\sqrt{3} + \sqrt{2})}^{2} = 5$

查看试题解析
6. 下列二次根式中，是最简二次根式的是（　　）

A、 $\sqrt{20}$ B、 $\sqrt{30}$ C、 $\sqrt{40}$ D、 $\sqrt{50}$

查看试题解析
7. 函数y＝ $\frac{\sqrt{x + 1}}{x}$ 中的自变量x的取值范围是（　　）

A、x＞0 B、x≥﹣1 C、x＞0且x≠﹣1 D、x≥﹣1且x≠0

查看试题解析
8. 实数 $a$ ， $b$ 在数轴上对应的点的位置如图所示那么 $\sqrt{{(b - a)}^{2}} + | a + b | - \sqrt[3]{b^{3}}$ 化简的结果（）

A、 $2 a + b$ B、 $b$ C、 $2 a - b$ D、 $3 b$

查看试题解析
9. 四巧板是一种类似七巧板的传统智力玩具，它是由一个长方形按如图1分割而成，这几个多边形的内角除了有直角外，还有45°、135°、270°角.小明发现可以将四巧板拼搭成如图2的T字形和V字形，那么T字形图中高与宽的比值 $\frac{h}{1}$ 为（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2} + 1}{2}$ C、 $\frac{4 + \sqrt{2}}{4}$ D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
10. 下列二次根式中，与 $\sqrt{3}$ 为同类二次根式的是（）

A、 $\sqrt{0.3}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{1}{18}}$

查看试题解析

二、填空题

11. 当x=时，代数式4- $\sqrt{x + 1}$ 有最大值，其最大值是

查看试题解析
12. 在下列式子 $\frac{1}{\sqrt{x - 2}}$ ， $\frac{1}{\sqrt{x - 3}}$ ， $\sqrt{x - 2}$ ， $\sqrt{x - 3}$ 中，x可以取2和3的是

查看试题解析
13. 若实数a满足 $\sqrt{2 a - 2}$ =4，则a的值为

查看试题解析
14. 已知实数a，b，c表示一个三角形的三边长，它们满足 $\sqrt{a - 3}$ +|b-3|+ $\sqrt{c - 4}$ =0，则该三角形的形状为

查看试题解析
15. 已知实数a，b，c在数轴上的位置如图所示，化简代数式 $\sqrt{a^{2}} - | a + c | + \sqrt{{(b - c)}^{2}} - | - b |$

查看试题解析
16. 若实数x ， y满足y＝3 $\sqrt{x - 5}$ +2 $\sqrt{5 - x}$ +8，则2x﹣y＝．

查看试题解析
17. 如图，长方形内有两个相邻的正方形，其面积分别为 $2$ 和 $8$ ，则图中阴影部分的面积为

查看试题解析

三、综合题

18.

(1)、已知二次根式 $\sqrt{3 - \frac{1}{2} x}$ ，求x的取值范围；

(2)、当x=-2时，求二次根式 $\sqrt{3 - \frac{1}{2} x}$ 的值；

(3)、若二次根式 $\sqrt{3 - \frac{1}{2} x}$ 的值为1，求x的值．

查看试题解析
19. 已知一个直角三角形的斜边长为41，一条直角边长为x．

(1)、用关于x的代数式表示这个直角三角形的另一条直角边长；

(2)、当x=40时，求另一条直角边的长．

查看试题解析
20. 阅读下列引例的解答过程：
已知x，y为实数，且y= $\sqrt{x - 2021} + \sqrt{2021 - x} + 1$ ，求x+y的值．

解：由题意，得x-2021≥0且2021-x≥0，

∴x≥2 021且x≤2 021，

∴x=2 021，∴y=1，

∴x+y=2 022．

结合引例，请挖掘下列问题中所蕴含的条件并解决问题：

(1)、已知y= $\frac{\sqrt{x - 4} + \sqrt{4 - x}}{2}$ -2．求(x+y)^y的值．

(2)、已知y= $\sqrt{- x^{2}}$ -1，求x-y的值．

(3)、已知|2021-x|+ $\sqrt{x - 2022}$ = x，求x-2021²的值．

查看试题解析
21. 解下列各题：

(1)、计算： $\sqrt[3]{- 27} + \sqrt{5} (\sqrt{5} - \frac{1}{\sqrt{5}})$ ；

(2)、计算： $| \sqrt{3} | + {(\sqrt{3} - \frac{1}{2})}^{2} - {(\sqrt{3} + \frac{1}{2})}^{2}$ ；

(3)、如图，点A是数轴上表示实数a的点．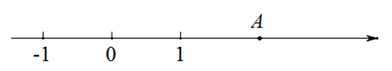

①用直尺和圆规在数轴上作出表示实数的 $\sqrt{2}$ 的点P；（保留作图痕迹，不写作法）

②利用数轴比较 $\sqrt{2}$ 和a的大小，并说明理由．

查看试题解析
22. 观察下列一组等式，解答后面的问题：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2}$ ﹣1，

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$

应用计算：

(1)、利用上面的方法进行化简： $\frac{1}{\sqrt{7} + \sqrt{6}}$ ；

(2)、归纳：根据上面的结论，找规律，请直接写出下列算式的结果： $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝；

(3)、拓展： $\frac{1}{\sqrt{101} + \sqrt{100}} + \frac{1}{\sqrt{102} + \sqrt{101}} + \frac{1}{\sqrt{103} + \sqrt{102}} + \dots \dots + \frac{1}{\sqrt{2021} + \sqrt{2020}}$ ＝．

查看试题解析
23.

(1)、计算： $(\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3}) + 1$ ；

(2)、计算： $\sqrt{125} + 9 \sqrt{\frac{2}{27}} - \frac{1}{2} \sqrt{24} + {(\sqrt{5})}^{2}$ ；

(3)、下面是甜甜同学进行实数运算的过程，认真阅读并完成相应的任务：
$\sqrt{\frac{9}{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$

$= \frac{\sqrt{9}}{\sqrt{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$ ……第一步

$= \frac{3 \sqrt{2}}{2} - 2 \sqrt{3} \times 2 \sqrt{6} + 2 \times 3 \sqrt{3} \times \sqrt{\frac{2}{3}}$ ……第二步

$= \frac{3 \sqrt{2}}{2} - 12 \sqrt{2} + 6 \sqrt{2}$ ……第三步

$= - \frac{9 \sqrt{2}}{2}$ ……第四步

任务一：以上化简步骤中第一步化简的依据是：；

任务二：第步开始出现错误，请写出错误的原因，该试运算正确结果是．

查看试题解析
24. 阅读材料：黑白双雄，纵横江湖；双剑合璧，天下无敌．这是武侠小说中的常见描述，其意是指两个人合在一起，取长补短，威力无比．在二次根式中也有这种相辅相成的“对子”，如： $(2 + \sqrt{3}) (2 - \sqrt{3}) = 1$ ， $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2}) = 3$ ，它们的积不含根号，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式，于是，二次根式除法可以这样理解：如： $\frac{1}{\sqrt{3}} = \frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 7 + 4 \sqrt{3}$ ．像这样，通过分子，分母同乘以一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化．
解决问题：

(1)、 $\sqrt{100} + \sqrt{99}$ 的有理化因式可以是， $\frac{1}{\sqrt{6} + \sqrt{5}}$ 分母有理化得．

(2)、计算：
①当 $a = \sqrt{3} + \sqrt{2}$ ， $b = \sqrt{3} - \sqrt{2}$ ，则 $a^{3} b^{2} + a^{2} b^{3} =$ ；

② $\frac{2}{\sqrt{2} + 1} + \frac{2}{\sqrt{3} + \sqrt{2}} + \frac{2}{2 + \sqrt{3}} + \frac{2}{\sqrt{5} + 2} + \cdot \cdot \cdot + \frac{2}{\sqrt{n} + \sqrt{n - 1}} =$ （ $n \geq 1$ 且 $n$ 为整数）．

(3)、根据你的推断，比较 $\sqrt{15} - \sqrt{14}$ 和 $\sqrt{14} - \sqrt{13}$ 的大小．

查看试题解析
25. 阅读下列材料，然后解答问题．
在进行二次根式的化简与计算时我们有时会遇到如： $\frac{3}{\sqrt{2}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：

$\frac{3}{\sqrt{2}}$ ＝ $\frac{3 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}$ ＝ $\frac{3 \sqrt{2}}{2}$ ； $\frac{2}{\sqrt{3} + 1}$ ＝ $\frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)}$ ＝ $\frac{2 \times (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}}$ = $\sqrt{3} - 1$ ．

以上将分母中的根号化去的过程，叫做分母有理化．

请参照以上方法化简下列各式：

(1)、 $\frac{5}{\sqrt{3}}$ ；

(2)、 $\frac{1}{\sqrt{2} - 1}$ ；

(3)、 $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + ... + \frac{1}{\sqrt{2021} + \sqrt{2019}}$ ．

查看试题解析
26. 已知： $a - b = 2 + \sqrt{2}$ ， $b - c = 2 - \sqrt{2}$ .
求：

(1)、a﹣c的值；

(2)、 $\frac{a^{2} + b^{2} + c^{2} - a b - a c - b c}{a b + b c - a c - b^{2}}$ 的值.

查看试题解析
27. 阅读下列解题过程：
例：若代数式 $\sqrt{{(2 - a)}^{2}} + \sqrt{{(a - 4)}^{2}} = 2$ ，求a的取值.

解：原式＝|a﹣2|+|a﹣4|，

当a＜2时，原式＝（2﹣a）+（4﹣a）＝6﹣2a＝2，解得a＝2（舍去）；

当2≤a＜4时，原式＝（a﹣2）+（4﹣a）＝2，等式恒成立；

当a≥4时，原式＝（a﹣2）+（a﹣4）＝2a﹣6＝2，解得a＝4；

所以，a的取值范围是2≤a≤4.

上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题：

(1)、当3≤a≤7时，化简： $\sqrt{{(3 - a)}^{2}} + \sqrt{{(a - 7)}^{2}}$ ＝；

(2)、请直接写出满足 $\sqrt{{(a - 1)}^{2}} + \sqrt{{(a - 6)}^{2}}$ ＝5的a的取值范围；

(3)、若 $\sqrt{{(a + 1)}^{2}} + \sqrt{{(a - 3)}^{2}}$ ＝6，求a的取值.

查看试题解析
28. 已知 $a = \sqrt{5} + 2 ， b = \sqrt{5} - 2$ .求下列式子的值：

(1)、 $a^{2} b + a b^{2}$

(2)、 $a^{2} - 3 a b + b^{2}$

查看试题解析