2021-2022学年初中数学北师大版七年级上册1-3章专题复习

试卷更新日期：2022-01-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 四个相同的小正方体组成的立体图形如图所示，它的主视图为（）

A、 B、 C、 D、

查看试题解析
2. 如下图，将三角形绕轴旋转一周，所得的立体图形从正面观察得到的图形是（）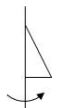

A、 B、 C、 D、

查看试题解析
3. 一个儿何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小正方块的个数，能符合题意表示该几何体的主视图的是（）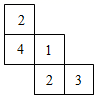

A、 B、 C、 D、

查看试题解析
4. 如图，这个几何体是将一个正方体中间挖出一个圆柱体后的剩余部分，该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 把立方体的六个面分别涂上六种不同的颜色，并画出朵数不等的花，各面上的颜色与花朵的朵数情况列表如下：现将上述大小相同，颜色、花朵分布完全样的四个立方体拼成一个水平放置的长方体，如图所示，那么长方体的下底面共有花朵数是（）

颜色

红

黄

蓝

白

紫

绿

花朵数

1

2

3

4

5

6

A、11 B、13 C、15 D、17

查看试题解析
6. 阿里巴巴数据显示，2021年天猫“双11”交易额超5403亿元，数据5403亿用科学记数法表示为（）

A、5403×10⁸ B、5.403×10¹⁰ C、5.403×10¹¹ D、0.5403×10¹²

查看试题解析
7. － $\frac{1}{2}$ 的绝对值是（）

A、－ $\frac{1}{2}$ B、2 C、－2 D、 $\frac{1}{2}$

查看试题解析
8. “东风快递，使命必达！”东风-41是我国目前最先进的洲际战略导弹，假设其最快飞行速度是25马赫，若每马赫速度为340米/秒，则用科学记数法表示东风-41的最快飞行速度为（）

A、8.5×10³米/秒 B、0.85×10⁴米/秒 C、8.5×10⁴米/秒 D、85×10³米/秒

查看试题解析
9. 计算 $(- 30) + 60$ 的结果等于（）

A、30 B、-90 C、90 D、-30

查看试题解析
10. 下列说法：①3²xy³是4次单项式； ②多项式2³x²y﹣3x²+1是六次三项式；
③将方程 $\frac{x - 1}{0.3} - \frac{x + 2}{0.5}$ =1.2中的分母化为整数，得 $\frac{10 x + 20}{5}$ =12；

④近似数4.3万精确到十分位．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 如图是由五个棱长均为1的正方体搭成的几何体，则它的左视图的面积为．

查看试题解析
12. 已知正方体的一个平面展开图如图所示，则在原正方体上“百”的对面是．

查看试题解析
13. 如图1，若在边长为a的正方形硬纸板的四角各剪掉一个矩形（图1中阴影部分，其中有两个小正方形），将剩余部分按图中的线条折成一个有盖的长方体盒子（图2）．若剪掉的一个小正方形的边长为b ，此时长方体盒子表面积是．

查看试题解析
14. 如图是正方体的一种展开图，其中每个面上都有一个数字，在原正方体中，与数字1相对面上的数字是。

查看试题解析
15. 一张长50cm，宽40cm的长方形纸板，在其四个角上分别剪去一个小正方形（边长相等且为整厘米数）后，折成一个无盖的长方体形盒子，这个长方体形盒子的容积最大为cm³.

查看试题解析
16. 如图，长方体的棱AB长为4，棱BC长为3，棱BF长为2，P为HG的中点，一只蚂蚁从点A出发，沿长方体的表面爬行到点 $P$ 处吃食物，那么它爬行的最短路程是.

查看试题解析
17. 将12.459精确到0.01得到的近似数是．

查看试题解析
18. 如果收入20元记作＋20元，那么支出50元记作元．

查看试题解析
19. 已知实数a，b，c表示一个三角形的三边长，它们满足 $\sqrt{a - 3}$ +|b-3|+ $\sqrt{c - 4}$ =0，则该三角形的形状为

查看试题解析
20. 若一个三棱锥的顶点个数为m、它的棱数为n，则（m+n－9）²⁰²¹的值为.

查看试题解析

三、计算题

21. 计算题、解方程

(1)、 $6 - 6 \times (- \frac{1}{2}) + | - 2 | \div {(- \frac{1}{3})}^{2}$

(2)、 $- 1^{4} - (2.5 - 2) \times \frac{1}{4} [4 - {(- 1)}^{3}]$

(3)、2(x－3)－3＝19－5(2x－4）

(4)、 $\frac{x}{0.2} - \frac{x - 0.1}{0.5} = 1$

查看试题解析

四、解答题

22. 已知 $\sqrt{x - 2 y + 9}$ 与|x-y-3|互为相反数，求 $\sqrt{x - y}$ 的值．

查看试题解析

五、综合题

23. 如图，一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．

(1)、填空： $a$ = ， b= ， c=；

(2)、先化简，再求值： $5 a^{2} b - [2 a^{2} b - 3 (2 a b c - a^{2} b)] + 4 a b c$

查看试题解析
24. 用棱长都为5cm的小立方块搭成几何体，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数．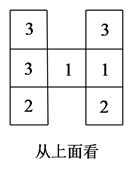

(1)、请你分别画出从正面和从左面看到的这个几何体的形状图；

(2)、若在所搭几何体的基础上（不改变原几何体中小立方块的位置），继续添加大小相同的小立方块，以搭成一个大正方体，至少还需要个小立方块；

(3)、①图中的几何体的表面积（包括与桌面接触的部分）为 ${cm}^{2}$ ；
②若新搭一个几何体，且满足如下三个条件：图中从上面看到的几何体的形状图不变，小立方块的总数不变，从上面看到的小正方形中的数字可以改变，则新搭几何体的表面积（包括与桌面接触的部分）最小值和最大值分别为 ${cm}^{2}$ ， ${cm}^{2}$ ．

查看试题解析
25. 如图1，现有一个棱长为20cm的立方体水槽放在桌面上，水槽内水的高度为acm，往水槽里放入棱长为10cm的立方体铁块.

(1)、求下列两种情况下a的值.
①若放入铁块后水面恰好在铁块的上表面，则a=cm；②若放入铁块后水槽恰好盛满（无溢出)，则a=cm；

(2)、若0≤a≤7.5，放入铁块后水槽内水面的高度为cm，(用含a的代数式表示）.

(3)、如图2，在水槽旁用管子连通一个底面在桌面上的圆柱形容器，内部底面积为
50cm² ，管口底部A离水槽内底面的高度为hcm (h>a)，水槽内放入铁块，水溢入圆柱形容器后，容器内水面与水槽内水面的高度差为4cm，若 a=15，求h的值.(水槽和容器的壁及底面厚度相同)

查看试题解析
26. 在一次青少年模型大赛中，小高和小刘各制作了一个模型，小高制作的是棱长为acm的正方体模型，小刘制作的是棱长为acm的正方体右上角割去一个长为3cm，宽为2cm，高为1cm的长方体模型（如图2）

(1)、用含a的代数式表示，小高制作的模型的各棱长度之和是；

(2)、若小高的模型各棱长之和是小刘的模型各棱长之和的 $\frac{5}{6}$ ，求a的值；

(3)、在（2）的条件下，
①图3是小刘制作的模型中正方体六个面的展开图，图中缺失的有一部分已经很用阴影表示，请你用阴影表示出其余缺失部分，并标出边的长度.

②如果把小刘的模型中正方体的六个面展开，则展开图的周长是 ▲ cm；请你在图方格中画出小刘的模型中正方体六个面的展开图周长最大时的图形.

查看试题解析
27. 阅读下列引例的解答过程：
已知x，y为实数，且y= $\sqrt{x - 2021} + \sqrt{2021 - x} + 1$ ，求x+y的值．

解：由题意，得x-2021≥0且2021-x≥0，

∴x≥2 021且x≤2 021，

∴x=2 021，∴y=1，

∴x+y=2 022．

结合引例，请挖掘下列问题中所蕴含的条件并解决问题：

(1)、已知y= $\frac{\sqrt{x - 4} + \sqrt{4 - x}}{2}$ -2．求(x+y)^y的值．

(2)、已知y= $\sqrt{- x^{2}}$ -1，求x-y的值．

(3)、已知|2021-x|+ $\sqrt{x - 2022}$ = x，求x-2021²的值．

查看试题解析
28. 已知，在数轴上a、b、c所对应的点分别为A、B、C点：c是最小的两位正整数，且a，b满足（a＋26）²＋|b＋c|＝0，请回答问题：

(1)、求a，b，c的值.

(2)、若P为该数轴的一点，PA＝3PB，求点P表示的数．

(3)、若点M从A出发，以每秒1个单位长度的速度向终点C移动，同时点N从B出发，以每秒3个单位长度向A点运动，N点到达A点后，再立即以同样的速度运动到终点C，当某一个点到达点C时另一个点停止运动。设点M运动时间为t秒，当t为何值时，M，N两点间的距离为4．

查看试题解析
29. 已知：b是最小的正整数，且a、b满足（c-5）²+|a+b|＝0，请回答问题：

(1)、请直接写出a、b、c的值：a＝；b＝；c＝．

(2)、a、b、c所对应的点分别为A、B、C，已知数轴上两点间的距离为这两点所表示的数的差的绝对值（或用这两点所表示数中较大的数减去较小的数），若点B与点C之间的距离表示为BC，点A与点B之间的距离表示为AB，试计算此时BC-AB的值．

(3)、在（1）（2）的条件下，点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动，则经过t秒钟时，请问：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请直接写出它的值．

查看试题解析
30. 阅读下面材料：
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a﹣b|；当A、B两点都不在原点时，

①如图2，点A、B都在原点的右边|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝b﹣a＝|a﹣b|；

②如图3，点A、B都在原点的左边，|AB|＝|OB|﹣|OA|＝|b|﹣|a|＝﹣b﹣（﹣a）＝|a﹣b|；

③如图4，点A、B在原点的两边，|AB|＝|OB|+|OA|＝|a|+|b|＝a+（﹣b）＝|a﹣b|

回答下列问题：

(1)、数轴上表示2和5的两点之间的距离是，数轴上表示﹣2和﹣5的两点之间的距离是，数轴上表示1和﹣3的两点之间的距离是；

(2)、数轴上表示x和﹣1的两点A和B之间的距离是，如果|AB|＝2，那么x为；

(3)、代数式|x+1|+|x﹣2|取最小值时，相应的整数x的取值是．

查看试题解析

颜色	红	黄	蓝	白	紫	绿
花朵数	1	2	3	4	5	6