浙教版备考2022年中考数学一轮复习专题7 二元一次方程（组）及其应用

试卷更新日期：2022-01-08 类型：一轮复习

进入出卷网下载

一、单选题

1. 下到方程组中，属于二元一次方程组的是（）

A、 ${\begin{array}{l} x + y = 5 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x + y = 2 \\ y - z = 6 \end{array}$ C、 ${\begin{array}{l} x y = 4 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x^{2} - 1 = 0 \\ x + y = 5 \end{array}$

查看试题解析
2. 已知 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} a x + b y = 7 \\ a x - b y = 1 \end{array}$ 的解，则﹣a^b的值为（　　）

A、﹣9 B、9 C、﹣8 D、8

查看试题解析
3. 如果|x﹣2|+（y+ $\frac{1}{3}$ ）²＝0，那么y^x的值为（　　）

A、 $\frac{1}{9}$ B、﹣ $\frac{1}{9}$ C、 $\frac{1}{6}$ D、﹣ $\frac{1}{6}$

查看试题解析
4. 关于x，y的方程组 ${\begin{cases} x - y = 3 a \\ 2 x + 4 y = 9 \end{cases}$ ，已知-4＜a＜0，则x+y的取值范围为（）

A、0＜x+y＜2 B、-1＜x+y＜3 C、0＜x+y＜4 D、-1＜x+y＜2

查看试题解析
5. 某市举办中学生足球赛，按比赛规则，每场比赛都要分出胜负，胜1场得3分，负一场扣1分，菁英队在8场比赛中得到12分，若设该队胜的场数为x，负的场数为y，则可列方程组为（）

A、 ${\begin{cases} x - y = 18 \\ 3 x - y = 12 \end{cases}$ B、 ${\begin{cases} x + y = 18 \\ 3 x + y = 12 \end{cases}$ C、 ${\begin{cases} x + y = 8 \\ 3 x + y = 12 \end{cases}$ D、 ${\begin{cases} x + y = 8 \\ 3 x - y = 12 \end{cases}$

查看试题解析
6. 有铅笔、练习本、圆珠笔三种学习用品．若购铅笔3支，练习本7本，圆珠笔1支共需31元；若购铅笔4支，练习本10本，圆珠笔1支共需42元．现购铅笔，练习本，圆珠笔各1个，共需（）

A、12元 B、10.5元 C、9.5元 D、9元

查看试题解析
7. 为迎接2022年北京冬奥会，某班开展了以迎冬奥为主题的体育活动，计划拿出200元钱全部用于购买甲、乙两种奖品（两种奖品都购买），奖励表现突出的学生，已知甲种奖品每件25元，乙种奖品每件10元，则购买方案有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
8. 已知关于x，y的方程组 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解为 ${\begin{matrix} x = 2 \\ y = 4 \end{matrix}$ ，则关于方程组 ${\begin{matrix} a_{1} (x + 1) + 2 b_{1} (y - 1) = 3 c_{1} \\ a_{2} (x + 1) + 2 b_{2} (y - 1) = 3 c_{2} \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = 5 \\ y = 7 \end{matrix}$ B、 ${\begin{matrix} x = 5 \\ y = 13 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 3 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = 7 \end{matrix}$

查看试题解析
9. 某车间每天能生产甲种零件120个或者乙种零件100个.3个甲种零件与2个乙种零件配成一套，要在27天内生产最多的成套产品，问甲、乙两种零件各生产几天？设甲种零件生产 $x$ 天，乙种零件生产 $y$ 天，下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 27 \\ 120 x = 100 y \end{array}$ B、 ${\begin{array}{l} x + y = 27 \\ 2 \times 120 x = 3 \times 100 y \end{array}$ C、 ${\begin{array}{l} x + y = 27 \\ 3 \times 120 x = 2 \times 100 y \end{array}$ D、 ${\begin{array}{l} x + y = 27 \\ 2 x = 3 y \end{array}$

查看试题解析
10. 将两块完全相同的长方体木块先按图1的方式放置，再按图2的方式放置，测得的数据如图所示．则桌子的高度 $h =$ （）

A、70 B、55 C、40 D、30

查看试题解析

二、填空题

11. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如 ﹣x²﹣4xy+4y²＝﹣x²+3y² ．

(1)、被捂住的多项式是；

(2)、当|x﹣2|+（y+1）²＝0时，被捂住的多项式的值为．

查看试题解析
12. 已知m为十位数字是8的三位数，且m-40n=24（n为自然数），则m的可能取值有种．

查看试题解析
13. 甲、乙、丙三人到某单人小火锅就餐，该店共有 $m$ 种配菜可以选择，每种配菜都有大盘菜、中盘菜、小盘菜这三种分量，价格分别为 $a$ 元、 $b$ 元和 $3$ 元， $3 < b < a \leq 8$ ， $a$ 、 $b$ 都为正整数.每个人都选择了所有 $m$ 种配菜，而且对于每一种配菜，三个人在分量上的选择都各个相同，结账时，甲乙两人都花费了 $53$ 元且两个在大盘菜的花费上各不相同，而丙共花费了 $54$ 元，那么丙在大盘菜上花费元.

查看试题解析
14. 若 $\sqrt{a^{2} - 3 a + 1} + b^{2} + 2 b + 1 = 0$ ，则 $a^{2} + \frac{1}{a^{2}} - | b |$ =.

查看试题解析
15. 某运输公司有核定载重量之比为 $3 ： 4 ： 5$ 的甲、乙、丙三种货车，该运输公司接到为某灾区免费运输物资任务，迅速按照各车型核定载重量将物资运往灾区，承担本次运输的三种货车数量相同，当这批物资送达灾区后，发现还需要一部分物资才能满足当地灾区的需要，于是该运输公司又安排部分甲、乙丙三种货车进行第二次运输，其中乙型车第二次送输的物资量是还需要运输的物资量的 $\frac{3}{5}$ ，丙型车两次运输的物资总量是两次运往灾区物资总量的 $\frac{2}{7}$ ，甲型车两次运输的物资总量与乙型车两次运输的物总量之比为 $2 ： 5$ ，则甲型车第一次与甲型车第二次运输的物资量之比是.

查看试题解析
16. 对 $x$ ， $y$ 定义一种新运算 $F$ ，规定： $F (x ， y) = (m x + n y) (3 x - y)$ （其中 $m$ ， $n$ 均为非零常数）.例如： $F (1 ， 1) = 2 m + 2 n$ ， $F (- 1 ， 0) = 3 m$ .当 $F (1 ， - 1) = - 8$ ， $F (1 ， 2) = 13$ ，则 $F (x ， y) =$ ；当 $x^{2} \neq y^{2}$ 时， $F (x ， y) = F (y ， x)$ 对任意有理数 $x$ ， $y$ 都成立，则 $m$ ， $n$ 满足的关系式是.

查看试题解析
17. 已知关于x，y的二元一次方程组 ${\begin{cases} x + y = a + b - 6 \\ x - y = a - b + 6 \end{cases}$ (a，b为实数)。

(1)、若x=2a-1，则a的值是；

(2)、若x，y同时满足ax+by+4=0，2x+5y-ay=0，则a+b的值是。

查看试题解析
18. 已知关于x、y的方程组 ${\begin{matrix} x + 3 y = 2 a + 4 \\ 2 x - y = 1 - 3 a \end{matrix}$ 的解都为非负数，且满足 $2 a + b = 5$ ， $2 \leq b \leq 5$ ，若 $z = a - b$ ，则z的取值范围是

查看试题解析
19. 采购员用一张1万元支票去购物，购单价为590元的A种物品若干件，又购单价为670元的B种物品若干件，其中B种件数多于A种件数，找回了几张100元和几张10元的（10元的不超过9张）.如把购A种物品和B种物品的件数互换，找回的100元和10元的钞票张数也恰好相反，则原来购B种物品件.

查看试题解析

三、综合题

20. 对 $x$ ， $y$ 定义一种新运算 $F (x ， y) = (a x + b y) (x + 3 y)$ （中 $a$ ， $b$ 均为非零常数）.例如： $F (1 ， 1) = 4 a + 4 b$ ；已知 $F (3 ， 1) = 0$ ， $F (0 ， 1) = - 9$ .

(1)、求 $a$ ， $b$ 的值；

(2)、若关于 $F$ 的不等式组 ${\begin{array}{l} F (3 t + 1 ， t) \geq k \\ F (6 t ， 1 - 2 t) < 27 \end{array}$ 恰好只有 $1$ 个整数解，求 $k$ 的取值范围.

查看试题解析
21. 新冠病毒来势汹汹，疫情刻不容缓，某企业接到一批制氧机订单急需大量工人生产制氧机，该企业招聘了一些工人，按照熟练程度，分为一级、二级、三级，已知一名一级工人和三名三级工人共同生产3天可完成54台，且一名一级工人每天比一名三级工人每天多生产6台。

(1)、求每名一级工人和每名三级工人每天分别生产多少台制氧机？

(2)、为了最大限度提高产量，该企业决定每月花费90000元（全部用完）招聘一、二、三级工人合计18人，其中各级工人至少一人，已知二级工人每天生产量是三级工人的2倍，一级、二级、三级工人每月的工资分别是6000元，5000元，3500元，问该企业应如何安排招聘方案，使得每天生产制氧机的台数最多？最多为多少台？

查看试题解析
22. 一个四位数，记千位和百位的数字之和为a，十位和个位的数字之和为b，如果a＝b，那么称这个四位数为“心平气和数”例如：1625，a＝1+6，b＝2+5，因为a＝b，所以，1625是“心平气和数”.

(1)、直接写出：最小的“心平气和数”是，最大的“心平气和数”；

(2)、将一个“心平气和数”的个位与十位的数字交换位置，同时将百位与千位的数字交换，称交换前后的这两个“心平气和数”为一组 “相关心平气和数”.例如：1625与6152为一组“相关心平气和数”，求证：任意的一组“相关心平气和数”之和是11的倍数.

(3)、求千位数字是个位数字的3倍，且百位数字与十位数字之和是14的倍数的所有“心平气和数”.

查看试题解析
23. 目前，新型冠状病毒在我国虽可控可防，但不可松懈某校欲购置规格分别为 $300 m l$ 和 $500 m l$ 的甲、乙两种免洗手消毒液若干瓶，已知购买1瓶甲和1瓶乙免洗手消毒液需要32元，购5瓶甲和3瓶乙免洗手消毒液需要120元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、该校在校师生共1000人，平均每人每天都需使用 $10 m l$ 的免洗手消毒液，若校方采购甲、乙两免洗手消毒液共花费4000元，则这批消毒液可使用多少天？

(3)、为节约成本，该校购买散装免洗手消毒液进行分装，现需将 $9.6 L$ 的免洗手消毒液全部装入最大容量分别为 $300 m l$ 和 $500 m l$ 的两种空瓶中（每瓶均装满），若分装时平均每瓶需损耗 $20 m l$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析
24. 某商场若购进2部甲型号手机和3部乙型号手机，共需7400元；若购进3部甲型号手机和5部乙型号手机，共需11700元.

(1)、求甲、乙型号手机每部的进价；

(2)、商场计划用不少于44400元且不多于50000元的资金购进这两种型号手机共30台.
①求有多少种进货方案；

②若每部甲，乙型号手机的售价分别为2500元，1950元，为了促销.商场决定每售出一部乙型号手机，返还顾客现金 $a$ 元（ $a \geq 150$ ，且 $a$ 为50的整数倍），要使每一种进货方案（全都售完）获利均不低于15300元，求 $a$ 的值.

查看试题解析
25. 某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算（小数部分无条件舍去） .

(1)、下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，

(2)、若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？

查看试题解析
26. 所谓完全平方式，就是对一个整式M，如果存在另一个整式N，使 $M = N^{2}$ ，则称M是完全平方式，如 $x^{4} = {(x^{2})}^{2}$ 、 $x^{2} + 2 x y + y^{2} = {(x + y)}^{2}$ ，则称 $x^{4}$ 、 $x^{2} + 2 x y + y^{2}$ 是完全平方式.

(1)、下列各式中是完全平方式的有.（填写编号）
① $a^{2} + 4 a + 4 b^{2}$ ② $4 x^{2}$ ③ $x^{2} - x y + y^{2}$ ④ $y^{2} - 10 y - 25$ ⑤ $x^{2} + 12 x + 36$

⑥ $\frac{1}{49} a^{2} - 2 a + 49$

(2)、证明：多项式 $x {(x + 4)}^{2} (x + 8) + 64$ 是一个完全平方式.

(3)、已知a、b、c是△ABC的三边长，满足 $a^{2} + b^{2} + 2 c^{2} = 2 c (a + b)$ ，判定△ABC的形状.

查看试题解析
27. 图1是一个三角形，分别连接这个三角形三边的中点得到图2；再分别连接图2中间小角形三边的中点，得到图3.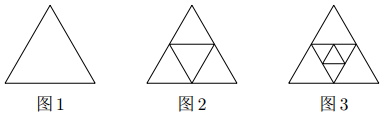

(1)、图2中共有个三角形，图3中共有三角形；

(2)、按上面的方法继续下去：
①第n个图形（图1是第一个图形）中共有多少个三角形（用含n的代数式表示）？如果某个图形有2021个三角形，求n的值.

②是否存在相邻两个图形的三角形的数量之和等于另一个图形的三角形的数量？说明理由.

查看试题解析
28. 我们知道，任意一个正整数 $x$ 都可以进行这样的分解： $x = m \times n$ （ $m$ ， $n$ 是正整数，且 $m \leq n$ ），在 $x$ 的所有这种分解中，如果 $m$ ， $n$ 两因数之差的绝对值最小，我们就称 $m \times n$ 是 $x$ 的最佳分解，并规定： $f (x) = \frac{n}{m}$ .例如： $18$ 可分解成 $1 \times 18$ ， $2 \times 9$ 或 $3 \times 6$ ，因为 $18 - 1 > 9 - 2 > 6 - 3$ ，所以 $3 \times 6$ 是 $18$ 的最佳分解，所以 $f (18) = \frac{3}{6} = \frac{1}{2}$

(1)、填空： $f (6) =$ ； $f (16) =$ ；

(2)、一个两位正整数 $t$ （ $t = 10 a + b$ ， $1 \leq a \leq b \leq 9$ ， $a$ ， $b$ 为正整数），交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为 $54$ ，求出所有的两位正整数；并求 $f (t)$ 的最大值；

(3)、填空：
① $f (2^{2} \times 3 \times 5 \times 7) =$ ；② $f (2^{4} \times 3 \times 5 \times 7) =$ ；

查看试题解析
29. 目前，新型冠状病毒在我国虽可控可防，但不可松懈某校欲购置规格分别为 $300 ml$ 和 $500 ml$ 的甲、乙两种免洗手消毒液若干瓶，已知购买1瓶甲和1瓶乙免洗手消毒液需要32元，购5瓶甲和3瓶乙免洗手消毒液需要120元.

(1)、求甲、乙两种免洗手消毒液的单价.

(2)、该校在校师生共1000人，平均每人每天都需使用 $10 ml$ 的免洗手消毒液，若校方采购甲、乙两免洗手消毒液共花费4000元，则这批消毒液可使用多少天？

(3)、为节约成本，该校购买散装免洗手消毒液进行分装，现需将 $9.6 L$ 的免洗手消毒液全部装入最大容量分别为 $300 ml$ 和 $500 ml$ 的两种空瓶中（每瓶均装满），若分装时平均每瓶需损耗 $20 ml$ ，请问如何分装能使总损耗最小，求出此时需要的两种空瓶的数量.

查看试题解析