2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.1 相交线与平行线
试卷更新日期:2022-01-07 类型:一轮复习
一、单选题
-
1. 如图,与∠1是内错角的是( )
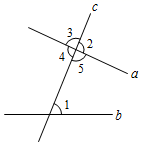 A、∠2 B、∠3 C、∠4 D、∠52. 如图, , ,则 的度数为( )
A、∠2 B、∠3 C、∠4 D、∠52. 如图, , ,则 的度数为( ) A、 B、 C、 D、3. 如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )
A、 B、 C、 D、3. 如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )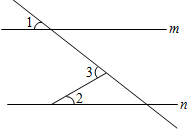 A、80° B、70° C、60° D、50°4. 如图,直线AB∥CD,∠M=90°,∠C=120°,则∠MPB=( )
A、80° B、70° C、60° D、50°4. 如图,直线AB∥CD,∠M=90°,∠C=120°,则∠MPB=( )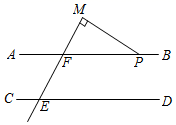 A、30° B、60° C、120° D、150°5. 如图,AM∥BN , ∠ACB=90°,∠MAC=35°,则∠CBN的度数是( )
A、30° B、60° C、120° D、150°5. 如图,AM∥BN , ∠ACB=90°,∠MAC=35°,则∠CBN的度数是( )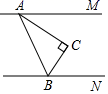 A、35° B、45° C、55° D、65°6. 已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数( )
A、35° B、45° C、55° D、65°6. 已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数( )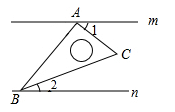 A、20° B、22° C、28° D、38°7. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )
A、20° B、22° C、28° D、38°7. 如图,直线a,b被直线c所截,a∥b,∠2=∠3,若∠1=80°,则∠4等于( )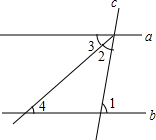 A、20° B、40° C、60° D、80°8. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )
A、20° B、40° C、60° D、80°8. 如图,将△ABC绕点B按逆时针方向旋转40°到△DBE(其中点D与点A对应,点E与点C对应),连接AD,若AD∥BC,则∠ABE的度数为( )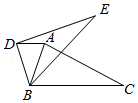 A、25° B、30° C、35° D、40°9. 如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )
A、25° B、30° C、35° D、40°9. 如图,AB CD,∠ABE= ∠EBF,∠DCE= ∠ECF,设∠ABE=α,∠E=β,∠F=γ,则α,β,γ的数量关系是( )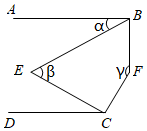 A、4β﹣α+γ=360° B、3β﹣α+γ=360° C、4β﹣α﹣γ=360° D、3β﹣2α﹣γ=360°10. 如图,已知直线 、 被直线 所截, ,E是直线 右边任意一点(点E不在直线 , 上),设 , .下列各式:① ,② ,③ ,④ , 的度数可能是( )
A、4β﹣α+γ=360° B、3β﹣α+γ=360° C、4β﹣α﹣γ=360° D、3β﹣2α﹣γ=360°10. 如图,已知直线 、 被直线 所截, ,E是直线 右边任意一点(点E不在直线 , 上),设 , .下列各式:① ,② ,③ ,④ , 的度数可能是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 如图所示,在△ABC中,∠A=90°,点D在AC边上,DE∥BC.若∠1=156°,则∠B=度.
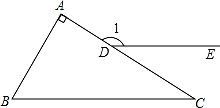 12. 把一把直尺和一块三角板如图放置,若∠1=42°,则∠2的度数为°.
12. 把一把直尺和一块三角板如图放置,若∠1=42°,则∠2的度数为°. 13. 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为9,△ABC的周长是14,则BC=.
13. 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若△ADE的周长为9,△ABC的周长是14,则BC=.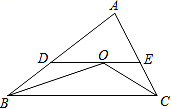 14. 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于
14. 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于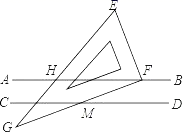 15. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.
15. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.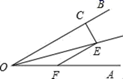 16. 如图,把一张长方形纸片 沿 折叠,点D与点C分别落在点 和点 的位置上, 与 的交点为G,若 ,则 为度.
16. 如图,把一张长方形纸片 沿 折叠,点D与点C分别落在点 和点 的位置上, 与 的交点为G,若 ,则 为度.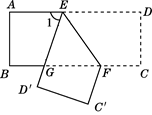 17. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .
17. 如图,直线l1∥l2 , ∠BAE=125°,∠ABF=85°,则∠1+∠2= .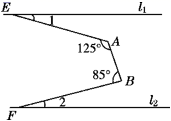 18. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为.
18. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为.
三、解答题
-
19. 如图, , ,试说明: .
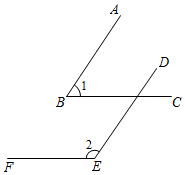 20. 如图,B,E分别是AC,DF上的点,AE∥BF,∠A=∠F.求证:∠C=∠D.
20. 如图,B,E分别是AC,DF上的点,AE∥BF,∠A=∠F.求证:∠C=∠D.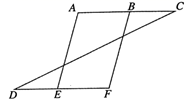 21. 如图,已知AD平分∠EAC,且AD∥BC,求证AB=AC.
21. 如图,已知AD平分∠EAC,且AD∥BC,求证AB=AC.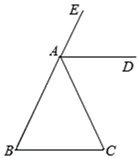 22. 如图,直线AB∥CD,点E在CD上,点O、点F在AB上,连接OE,过点F作FH⊥OE于点H.
22. 如图,直线AB∥CD,点E在CD上,点O、点F在AB上,连接OE,过点F作FH⊥OE于点H. (1)、尺规作图:作∠EOF的角平分线OG交CD于点G;(不写作法,保留作图痕迹,并标明字母)(2)、在(1)的条件下,已知∠OFH=20°,求∠OGD的度数.23. 如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.
(1)、尺规作图:作∠EOF的角平分线OG交CD于点G;(不写作法,保留作图痕迹,并标明字母)(2)、在(1)的条件下,已知∠OFH=20°,求∠OGD的度数.23. 如图,∠AOB是平角,∠DOE=90°,OC平分∠DOB.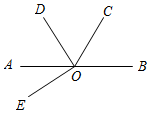 (1)、若∠AOE=32°,求∠BOC的度数;(2)、若OD是∠AOC的角平分线,求∠AOE的度数.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)、若∠AOE=32°,求∠BOC的度数;(2)、若OD是∠AOC的角平分线,求∠AOE的度数.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. (1)、CD与EF平行吗?为什么?
(1)、CD与EF平行吗?为什么?
(2)、CD与EF平行吗?为什么?(3)、如果∠1=∠2,且∠3=115°,求∠ACB的度数.25. 在四边形ABCD中,∠A=∠C=90°.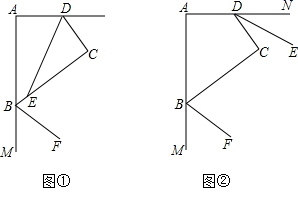 (1)、求:∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC , BF平分∠CBM , 写出DE与BF的位置关系.(3)、如图②,若BF , DE分别平分∠ABC , ∠ADC的外角,写出BF与DE的位置关系,对(2)和(3)任选一个加以证明.26. 如图,四边形ABCD中,AB∥CD,∠C=110°.E为BC的中点,直线FG经过点E,DG⊥FG于点G,BF⊥FG于点F.
(1)、求:∠ABC+∠ADC=°;(2)、如图①,若DE平分∠ADC , BF平分∠CBM , 写出DE与BF的位置关系.(3)、如图②,若BF , DE分别平分∠ABC , ∠ADC的外角,写出BF与DE的位置关系,对(2)和(3)任选一个加以证明.26. 如图,四边形ABCD中,AB∥CD,∠C=110°.E为BC的中点,直线FG经过点E,DG⊥FG于点G,BF⊥FG于点F.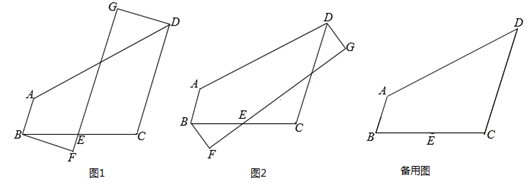 (1)、如图1,当∠BEF=70°时,求证:DG=BF;(2)、如图2,当∠BEF≠70°时,若BC=DC,DG=BF,请直接写出∠BEF的度数;(3)、当DG-BF的值最大时,直接写出∠BEF的度数.27.(1)、(问题)如图①,点C是线段AB上一点,点D,E分别是线段AC,BC的中点,若线段AB=26cm,则线段DE的长为 cm.
(1)、如图1,当∠BEF=70°时,求证:DG=BF;(2)、如图2,当∠BEF≠70°时,若BC=DC,DG=BF,请直接写出∠BEF的度数;(3)、当DG-BF的值最大时,直接写出∠BEF的度数.27.(1)、(问题)如图①,点C是线段AB上一点,点D,E分别是线段AC,BC的中点,若线段AB=26cm,则线段DE的长为 cm. (2)、(拓展)在(问题)中,若把条件“如图①,点C是线段AB上一点”改为“点C是直线 AB上一点”,其余条件不变,则(问题)中DE的长是否会发生变化?请画出示意图并求解.(3)、(应用)如图②,∠AOB=α,点C在∠AOB内部,射线OM,ON分别平分∠AOC,∠BOC,则∠MON的大小为(用含字母α的式子表示).
(2)、(拓展)在(问题)中,若把条件“如图①,点C是线段AB上一点”改为“点C是直线 AB上一点”,其余条件不变,则(问题)中DE的长是否会发生变化?请画出示意图并求解.(3)、(应用)如图②,∠AOB=α,点C在∠AOB内部,射线OM,ON分别平分∠AOC,∠BOC,则∠MON的大小为(用含字母α的式子表示).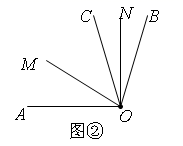 (4)、如图③,在(3)中,若点C在∠AOB外部,且射线OC与射线OB在OA所在直线的同侧,其他条件不变,则(1)中的结论是否成立,若成立,请写出求解过程;若不成立,请说明理由.
(4)、如图③,在(3)中,若点C在∠AOB外部,且射线OC与射线OB在OA所在直线的同侧,其他条件不变,则(1)中的结论是否成立,若成立,请写出求解过程;若不成立,请说明理由.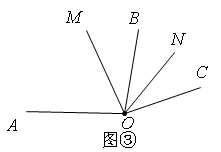 28. 如图 ,MN∥PQ,直线 与 、 分别交于点 、 ,点 在直线 上,过点 作 ,垂足为点 .
28. 如图 ,MN∥PQ,直线 与 、 分别交于点 、 ,点 在直线 上,过点 作 ,垂足为点 .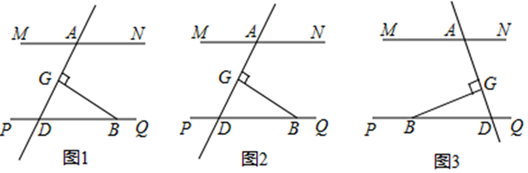 (1)、求证: ;(2)、若点 在线段 上 不与 、 、 重合 ,连接 , 和 的平分线交于点 ,请在图 中补全图形,猜想并证明 与 的数量关系;(3)、若直线 的位置如图 所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出 与 的数量关系.
(1)、求证: ;(2)、若点 在线段 上 不与 、 、 重合 ,连接 , 和 的平分线交于点 ,请在图 中补全图形,猜想并证明 与 的数量关系;(3)、若直线 的位置如图 所示,(2)中的结论是否成立?若成立,请证明;若不成立,请直接写出 与 的数量关系.