陕西省中考数学历年真题模拟题汇编——三角形
试卷更新日期:2022-01-07 类型:二轮复习
一、单选题
-
1. 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( )
 A、3 B、6 C、3 D、2. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
A、3 B、6 C、3 D、2. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
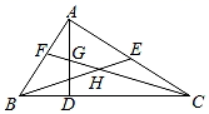 A、①②③④ B、①②③ C、②④ D、①③3. 如图,AB∥EF,∠B=75°,∠FDC=135°,则∠C的度数等于( )
A、①②③④ B、①②③ C、②④ D、①③3. 如图,AB∥EF,∠B=75°,∠FDC=135°,则∠C的度数等于( ) A、30° B、35° C、45° D、60°4. 如图,在 中, , , 平分 交 于点 , 的垂直平分线 交 于点 ,交 于点 ,若 ,则 的长为( )
A、30° B、35° C、45° D、60°4. 如图,在 中, , , 平分 交 于点 , 的垂直平分线 交 于点 ,交 于点 ,若 ,则 的长为( ) A、 B、 C、 D、5. 如图, 中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A、 B、 C、 D、5. 如图, 中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( ) A、4 B、3 C、5 D、66. 如图,菱形 对角线 , 交于点 , ,过点 作 交 的延长线于点 .若菱形 的面积为4,则菱形的边长为( )
A、4 B、3 C、5 D、66. 如图,菱形 对角线 , 交于点 , ,过点 作 交 的延长线于点 .若菱形 的面积为4,则菱形的边长为( ) A、 B、2 C、 D、47. 如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A、 B、2 C、 D、47. 如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( ) A、2 B、 C、3 D、8. 如图,已知 中,CD⊥AB,垂足为D,CE平分∠ACD交AD于E,若CD=12,BC=13,且 的面积为48,则点E到AC的距离为( )
A、2 B、 C、3 D、8. 如图,已知 中,CD⊥AB,垂足为D,CE平分∠ACD交AD于E,若CD=12,BC=13,且 的面积为48,则点E到AC的距离为( ) A、5 B、3 C、4 D、19. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或
A、5 B、3 C、4 D、19. 在平面直角坐标系中,有两条抛物线关于原点中心对称,且它们的顶点相距 个单位长度,若其中一条抛物线的函数表达式为 ,则 的值为( )A、 或 B、 或 C、 或 D、 或二、填空题
-
10. 在平面直角坐标系中,A为反比例函数y=﹣ (x>0)图象上一点,点B的坐标为(4,0),O为坐标原点,若 的面积为6,则点A的坐标为.11. 如图,AD,BE在AB的同侧,AD=4,BE=4,AB=8,点C为AB的中点,若∠DCE=120°,则DE的最大值是.
 12. 如图,在平行四边形 中, , ,其高 ,沿虚线 将纸片剪成两个面积相等的部分,若 ,则 的长为.
12. 如图,在平行四边形 中, , ,其高 ,沿虚线 将纸片剪成两个面积相等的部分,若 ,则 的长为. 13. 如图,在边长为13的菱形ABCD中,对角线BD=24,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.
13. 如图,在边长为13的菱形ABCD中,对角线BD=24,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.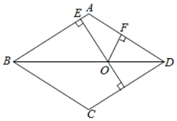 14. 如图,在菱形 中, ,点 是菱形 内或边上的一点,且 ,连接 ,则 面积的最小值为.
14. 如图,在菱形 中, ,点 是菱形 内或边上的一点,且 ,连接 ,则 面积的最小值为. 15. 如图,在△ABC中,∠ACB=90°,AB=4,点O是AB的中点,以BC为直角边向外作等腰Rt△BCD,连接OD,当OD取最大值时,则∠ODB的度数是.
15. 如图,在△ABC中,∠ACB=90°,AB=4,点O是AB的中点,以BC为直角边向外作等腰Rt△BCD,连接OD,当OD取最大值时,则∠ODB的度数是.
三、作图题
-
16. 如图,在 中.请用尺规作图法,求作一个以 为内角的菱形 ,使顶点E、F、G分别在 、 、 边上.
 17. 如图,在 中, ,用尺规在 上求作一点 ,使 到边 , 的距离相等(不写作法,保留作图痕迹).
17. 如图,在 中, ,用尺规在 上求作一点 ,使 到边 , 的距离相等(不写作法,保留作图痕迹).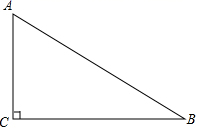 18. 如图,在 中,∠A=30°,请用尺规作图法,在AC边上求作一点M,使得AM=2BM.(不写作法,保留作图痕迹)
18. 如图,在 中,∠A=30°,请用尺规作图法,在AC边上求作一点M,使得AM=2BM.(不写作法,保留作图痕迹)
四、解答题
-
19. 如图,在四边形 中, ,连接 ,点 在 上,连接 ,若 , ,求证: .
 20. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在DB的延长线上,DE=BC,∠1=∠2,求证:DF=AB.
20. 如图,在△ABC中,∠ABC=90°,BD⊥AC于点D,点E在DB的延长线上,DE=BC,∠1=∠2,求证:DF=AB.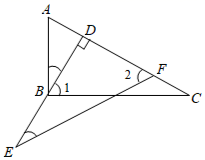 21. 如图,AB∥CF,D,E分别是AB,AC上的点,DE=EF.求证:△ADE≌△CFE.
21. 如图,AB∥CF,D,E分别是AB,AC上的点,DE=EF.求证:△ADE≌△CFE.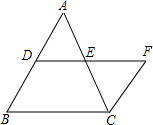 22. 如图,点D在等边 的边 上,作 ,交 于点G,点F在边 上,连接 并延长,交 的延长线于点E,且 .求证: .
22. 如图,点D在等边 的边 上,作 ,交 于点G,点F在边 上,连接 并延长,交 的延长线于点E,且 .求证: . 23. 如图,在△ABC中,AB=BC,点E为AC的中点,且∠DCA=∠ACB,DE的延长线交AB于点F。求证:AF=CD。
23. 如图,在△ABC中,AB=BC,点E为AC的中点,且∠DCA=∠ACB,DE的延长线交AB于点F。求证:AF=CD。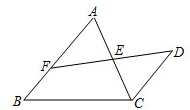
五、综合题
-
24. 如图,△ABC中,点D、E在边BC上,∠ADC=∠AEB,CD=BE.求证:∠BAD=∠CAE.
 25. 如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F.
25. 如图,△ABD和△BCE都是等边三角形,∠ABC<105°,AE与DC交于点F. (1)、求证:AE=DC;(2)、求∠BFE的度数;(3)、若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.26. 如图, , , .求证: .
(1)、求证:AE=DC;(2)、求∠BFE的度数;(3)、若AF=9.17cm,BF=1.53cm,CF=7.53cm,求CD.26. 如图, , , .求证: . 27. 如图,△ABD和△BCE都为等边三角形,连接AE、CD.求证:AE=DC.
27. 如图,△ABD和△BCE都为等边三角形,连接AE、CD.求证:AE=DC. 28. 如图,已知AB=AC,E为AB上一点,ED∥AC,BD=CD,求证:ED=AE.
28. 如图,已知AB=AC,E为AB上一点,ED∥AC,BD=CD,求证:ED=AE. 29.(1)、(1)问题发现
29.(1)、(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE.

填空:
①∠AEB的度数为;
②线段AD、BE之间的数量关系为 .
(2)、拓展研究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
(3)、解决问题如图3,在正方形ABCD中,CD=2 ,若点P满足PD=2,且∠BPD=90°,请直接写出点A到BP的距离.