湘教版数学八年级上册期末简答题综合测评

试卷更新日期：2022-01-07 类型：复习试卷

进入出卷网下载

一、计算题

1. 解不等式组： ${\begin{array}{l} 2 x + 3 \geq x + 9 \\ \frac{2 x + 5}{3} > 2 - x \end{array}$

查看试题解析
2.

(1)、解不等式组 ${\begin{matrix} 4 (x + 1) \leq 7 x + 13 \\ x - 4 < \frac{x - 8}{3} \end{matrix}$ ；

(2)、解方程： $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$ .

查看试题解析
3. 计算： $\frac{2}{\sqrt{2} - 1} - {(\sqrt{2} - 1)}^{2} + {(\frac{1}{\sqrt{2} - 3})}^{0}$ ．

查看试题解析
4. 计算

(1)、 $\sqrt[3]{- 8} - | 1 - \sqrt{2} | + {(- \frac{1}{2})}^{- 1} \times {(- 2007)}^{0}$ ；

(2)、 $\sqrt{27} \div \sqrt{\frac{3}{2}} - {(\sqrt{2} - 1)}^{2}$ .

查看试题解析
5. 计算： $\sqrt{{(- 3)}^{2}}$ ﹣ $\sqrt{8}$ ＋| $\sqrt{50}$ ﹣3|．

查看试题解析

二、解答题

6. 已知关于x的方程 $\frac{x - 4}{x - 3} - m - 4 = \frac{m}{3 - x}$ 无解，求m的值.

查看试题解析
7. 解方程： $\frac{2}{x^{2} - 1} + 1 = \frac{x}{x - 1}$ ．

查看试题解析
8. 如图，在△ABC 中，∠ABC=60°，∠ACB=82°，延长CB至D ，使DB=BA ，延长BC至E ，使CE=CA ，连接AD ， AE ．求∠D ， ∠E ， ∠DAE 的度数．

查看试题解析
9. 如图，在 $△ A B C$ 中， $A D$ ， $A E$ 分别是 $Δ A B C$ 的高和角平分线，若 $∠ A B C = 30 °$ ， $∠ A C B = 60 °$ ，求 $∠ D A E$ 的度数．

查看试题解析
10. 如图，在△ABC中，AB=AC，D是AB的中点，且DE⊥AB，△BCE的周长为8cm，且AC﹣BC=2cm，求AB、BC的长．

查看试题解析
11. 如图，已知∠ABC=50°，∠ACB=60°，BO、CO分别是∠ABC和∠ACB的平分线．求∠BOC的度数．

查看试题解析
12. 如图，点 $B 、 C 、 E 、 F$ 在一条直线上， $AB = CD ， AE = DF ， BF = CE$ ，求证： $∠ A = ∠ D$ .

查看试题解析
13. 如图，点D、B分别在∠A的两边上，C是∠A内一点，AB = AD，BC = CD，CE⊥AD于E，CF⊥AF于F.求证：CE = CF.

查看试题解析
14. 如图，已知 $A B = A D ， A C = A E$ ， $∠ 1 = ∠ 2$ ，求证 $∠ C = ∠ E$ .

查看试题解析
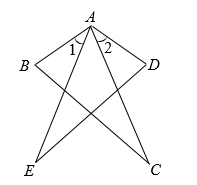15. 如图，已知AE⊥BC，AD平分∠BAE，∠ADB＝110°，∠CAE＝20°，求∠BAC和∠B的度数．

查看试题解析
16. 如图，∠ABC＝∠DCB，BD、CA分别平分∠ABC、∠DCB．求证：AC＝DB．

查看试题解析
17. 如图，在△ABC中，AB=AC，BD=CD，DE⊥AB，DF⊥AC，垂足分别为点E、F．
求证：△BED≌△CFD．

查看试题解析
18. 已知在△ABC中，AB＝AC，且线段BD为△ABC的中线，线段BD将△ABC的周长分成12和6两部分，求△ABC三边的长．

查看试题解析
19. 如图，在△ABC中，D是BC边上一点，AD=BD=AC，∠BAC=63⁰ ，求∠DAC的度数.

查看试题解析
20. 如图，已知AB＝AD ， ∠ABC＝∠ADC ，则∠1＝∠2，试说明理由．

查看试题解析

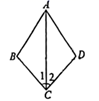
三、综合题

21. 解答下列各题：

(1)、计算： $\frac{1}{a - 1} + \frac{2}{1 - a^{2}}$ ；

(2)、先化简，再求值： $\frac{x^{2} - 4 x + 4}{x + 1} \div (\frac{3}{x + 1} - x + 1)$ ，请从不等式组 ${\begin{array}{l} 5 - 2 x \geq 1 \\ x + 2 \geq 0 \end{array}$ 的整数解中选择一个合适的值代入求值．

查看试题解析
22. 某商品经销店欲购进A、B两种纪念品，用320元购进的A种纪念品与用400元购进的B种纪念品的数量相同，每件B种纪念品的进价比A种纪念品的进价贵10元．

(1)、求A、B两种纪念品每件的进价分别为多少？

(2)、若该商店A种纪念品每件售价45元，B种纪念品每件售价60元，这两种纪念品共购进200件，这两种纪念品全部售出后总获利不低于1600元，求A种纪念品最多购进多少件．

查看试题解析

23. 今年南方某地发生特大洪灾，政府为了尽快搭建板房安置灾民，给某厂下达了生产A种板材48000m²和B种板材24000m²的任务.

(1)、如果该厂安排210人生产这两种板材，每人每天能生产A种板材60m²或B种板材40m² ，请问：应分别安排多少人生产A种板材和B种板材，才能确保同时完成各自的生产任务？

(2)、某灾民安置点计划用该厂生产的两种板材搭建甲、乙两种规格的板房共400间，已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示：

板房	A种板材（m²）	B种板材（m²）	安置人数
甲型	108	61	12
乙型	156	51	10

问这400间板房最多能安置多少灾民？

查看试题解析

24. 接种新冠病毒疫苗，建立全民免疫屏障，是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心，据调查得知，2辆 $A$ 型冷链运输车与3辆 $B$ 型冷链运输车一次可以运输600盒：5辆 $A$ 型冷链运输车与6辆 $B$ 型冷链运输车一次可以运输1350盒.

(1)、求每辆 $A$ 型车和每辆 $B$ 型车一次可以分别运输多少盒疫苗.

(2)、计划用两种冷链运输车共12辆运输这批疫苗， $A$ 型车一次需费用5000元， $B$ 型车一次需费用3000元.若运输物资不少于1500盒，且总费用小于54000元.请你列出所有运输方案，并指出哪种方案所需费用最少，最少费用是多少？

查看试题解析
25. 某城市平均每天产生垃圾700吨，由甲、乙两个垃圾处理厂处理，已知甲厂每小时处理垃圾55吨，需费用550元；乙厂每小时可处理垃圾45吨，需费用495元.

(1)、甲、乙两厂同时处理该城市的垃圾，每天需要几小时完成？

(2)、如果规定该城市每天用于处理垃圾的费用不得超过7370元，甲厂每天处理垃圾至少需要多少小时？

查看试题解析
26. 双十一前，妈妈购买了甲种物品15个，乙种物品20个，共花费250元，已知购买一个甲种物品比购买一个乙种物品多花费5元．

(1)、求双十一前购买一个甲种、一个乙种物品各需多少元？

(2)、双十一期间，甲种物品售价比上一次购买时减价2元，乙种物品按上一次购买时售价的8折出售．如果妈妈此时再次购买甲、乙两种物品共35个，总费用不超过225元，求至多需要购买多少个甲种物品？

查看试题解析