湖北省武汉市青山区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2022-01-06 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 在四个数－1，0，1，2中，最小的数是（   ）
    A、2 B、0 C、1 D、－1

    查看试题解析

  • 2. 下列方程，是一元一次方程的是 （   ）
    A、2x－3＝x B、x－y＝2 C、x－ 1x ＝1 D、x2－2x＝0

    查看试题解析

  • 3. 方程 8−3x=ax−4 的解是 x=3 ，则 a 的值是（   ）.
    A、1 B、-1 C、-3 D、3

    查看试题解析

  • 4. 下列四个几何体中，从左面看是圆的几何体是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 检测4个排球，其中超过标准的克数记为正数，不足的克数记为负数.从轻重的角度看，哪个球更接近标准（   ）
    A、－2.4 B、＋0.7 C、3.2 D、－0.5

    查看试题解析

  • 6. 如图，下列说法错误的是（   ）

    A、∠1与∠AOC表示的是同一个角； B、∠a表示的是∠BOC C、∠AOB也可用∠O表示； D、∠AOB是∠AOC与∠BOC的和

    查看试题解析

  • 7. 已知∠α＝70°18'，则∠α的补角是（   ）
    A、110°42′ B、109°42′ C、20°42′ D、19°42′

    查看试题解析

  • 8. 《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价各几何？译文为：现有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？这个物品的价格是多少？设这个物品的价格是x元，则可列方程为（   ）
    A、8x+3=7x+4 B、8x﹣3=7x+4 C、x−38=x+47 D、x+38=x−47

    查看试题解析

  • 9. 下列说法：①延长射线AB；              

     ②射线OA与射线AO是同一条射线；

    ③若（a－6）x3－2x2－8x－1是关于x的二次多项式，则a＝6；

    ④已知A，B，C三个点，过其中任意两点作一条直线，可作出1或3条直线.

    其中正确的个数有（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 10. 如图，按照上北下南，左西右东的规定画出方向十字线，∠AOE＝m°，∠EOF＝90°，OM、ON分别平分∠AOE和∠BOF，下面说法：

    ①点E位于点O的北偏西m°；②图中互余的角有4对；③若∠BOF＝4∠AOE，则∠DON＝54°；④若 ∠MON∠AOE+∠BOF=n ，则n的倒数是 23 ，其中正确有（   ）

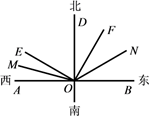    A、3个 B、2个 C、1个 D、0个

    查看试题解析

二、填空题

  • 11. 某地一天早晨的气温是－2℃，中午温度上升了8℃，则中午的气温是℃.

    查看试题解析

  • 12. 用两个钉子就可以把木条固定在墙上，这种现象的理论依据是.

    查看试题解析

  • 13. 中国的陆地面积约为9 600 000km2 ， 把9 600 000用科学记数法表示为 .

    查看试题解析

  • 14. 如图，是一个正方体的表面展开图，若正方体相对两个面上的数互为相反数，则3x－y的值为.

    查看试题解析

  • 15. 某糕点厂要制作一批盒装蛋糕，每盒中装2块大蛋糕和4块小蛋糕，制作1块大蛋糕要用0.05kg面粉，1块小蛋糕要用0.02kg面粉.现共有面粉450kg，用kg面粉制作大蛋糕，才能生产最多的盒装蛋糕.

    查看试题解析

  • 16. 如图，是一个运算的流程图，输入正整数x的值，按流程图进行操作并输出y的值.例如，若输入x＝10，则第一次输出y＝5.若输入某数x后，第二次输出y＝3，则输入的x的值为.

    查看试题解析

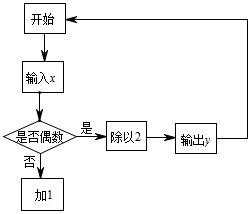
三、解答题

  • 17. 计算：
    (1)、（－1）10×2＋(－2)3÷4      
    (2)、(8a－7b)－2(4a－5b)

    查看试题解析

  • 18. 解方程：
    (1)、5x＝3x－6                           
    (2)、x−12−3−x3=1

    查看试题解析

  • 19. 如图，点C是线段AB外一点.请按下列语句画图.

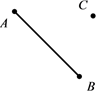    (1)、①画射线CB；

    ②反向延长线段AB；

    ③连接AC，并延长至点D，使CD＝BC；

    (2)、试比较AD与AB的大小，并简单说明理由.

    查看试题解析

  • 20. 下表是某校七、八年级某月课外兴趣小组活动时间统计表，其中七、八年级同一兴趣小组每次活动时间相同.

    年级

    课外小组活动总时间/ h

    文艺小组活动次数

    科技小组活动次数

    七年级

    18.6

    6

    7

    八年级

    15

    5

    5
    (1)、文艺小组和科技各活动1次，共用时h；
    (2)、求文艺小组每次活动多少h？

    查看试题解析

  • 21. 如图1，将长方形笔记本活页纸片的一角对折，使角的顶点A落在A′处，BC为折痕.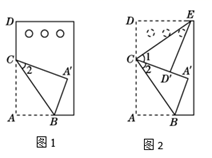

    (1)、若∠ACB＝35°.

    ① 求∠A′CD的度数；

    ② 如图2，若又将它的另一个角也斜折过去，并使CD边与CA′重合，折痕为CE.求∠1和∠BCE的度数；

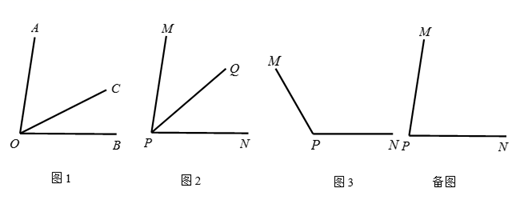
    (2)、在图2中，若改变∠ACB的大小，则CA′的位置也随之改变，则∠BCE的大小是否改变？请说明理由.

    查看试题解析

  • 22.   2020年“双十一”购物节，某商店将甲种商品降价30%，乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为2400元，顾客A参加此次活动购买甲、乙两种商品各一件，共付1830元.
    (1)、求甲、乙两种商品的原销售单价各是多少元？
    (2)、若商店在这次与顾客A的交易中，甲种商品亏损25%，乙种商品盈利25%，求商店在这次与顾客A的交易中总的盈亏情况.

    查看试题解析

  • 23. （学习概念） 如图1，在∠AOB的内部引一条射线OC，则图中共有3个角，分别是∠AOB、∠AOC和∠BOC.若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“好好线”.
    (1)、①如图2，若∠MPQ＝∠NPQ，则射线PQ▲ ∠MPN的“好好线”（填“是”或“不是”）；

    ②若∠MPQ≠∠NPQ，∠MPQ＝α，且射线PQ是∠MPN的“好好线”，请用含α的代数式表示∠MPN；

    (2)、（拓展提升）

    如图3，若∠MPN＝120°，射线PQ绕点P从PN位置开始，以每秒12°的速度逆时针旋转，旋转的时间为t秒.当PQ与PN成110°时停止旋转.同时射线PM绕点P以每秒6°的速度顺时针旋转，并与PQ同时停止. 当PQ、PM其中一条射线是另一条射线与射线PN的夹角的“好好线”时，则t＝秒.

    查看试题解析

  • 24. 已知线段AB＝m，CD＝n，线段CD在直线AB上运动（A在B的左侧，C在D的左侧），且m，n满足|m－12|＋（n－4）2＝0.

    (1)、m＝ ， n＝；
    (2)、点D与点B重合时，线段CD以2个单位长度/秒的速度向左运动.

    ①如图1，点C在线段AB上，若M是线段AC的中点，N是线段BD的中点，求线段MN的长；

    ②P是直线AB上A点左侧一点，线段CD运动的同时，点F从点P出发以3个单位/秒的向右运动，点E是线段BC的中点，若点F与点C相遇1秒后与点E相遇.试探索整个运动过程中，FC－5DE是否为定值，若是，请求出该定值；若不是，请说明理由.

    查看试题解析