浙江省杭州市萧山区六校2021-2022学年八年级上学期12月份独立作业数学试题

试卷更新日期：2022-01-06 类型：月考试卷

进入出卷网下载

一、填空题（本大题有10小题，每小题3分，共30分）

1. 下列长度的三条线段，能组成三角形的是（）

A、3，5，7 B、3，6，10 C、5，5，11 D、5，6，11

查看试题解析
2. 若 $a > b$ 成立，则下列不等式成立的是（）

A、 $- a > - b$ B、 $- a + 1 > - b + 1$ C、 $2 a - 1 > 2 b - 1$ D、 $m^{2} a > m^{2} b$

查看试题解析
3. 已知点A $(a ， 2)$ 关于 $x$ 轴的对称点A’与点B $(3 ， b)$ 关于 $y$ 轴的对称点B’重合，则 $a + b =$ （）

A、5 B、1 C、-1 D、-5

查看试题解析
4. 如图，点F在BC， $△ ABC ≌ △ AEF$ ， $AB = AE$ ， $∠ B = ∠ E$ ，则对于以下结论不正确的是（）

A、 $AC = AF$ B、 $∠ FAB = ∠ B$ C、 $EF = BC$ D、 $∠ AFC = ∠ ACF$

查看试题解析
5. 有下列四个命题是真命题的个数有（）个.
①垂直于同一条直线的两条直线互相垂直；②有一个角为60°的等腰三角形是等边三角形； ③三边长为 $\sqrt{14}$ ， $\sqrt{5}$ ，3的三角形为直角三角形；④顶角和底边对应相等的两个等腰三角形全等。

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，在 $Δ ABC$ 中， $∠ ACB = 90 °$ ， $∠ B = 30 °$ ， $AD$ 平分 $∠ BAC$ ， $E$ 是 $AD$ 中点，若 $BD = a$ ，则 $CE$ 的长为（）

A、 $\frac{1}{3} a$ B、 $\frac{1}{2} a$ C、 $\frac{2}{3} a$ D、 $\frac{3}{4} a$

查看试题解析
7. 已知关于x的不等式组的 ${\begin{cases} x - a \geq b \\ 2 x - a < 2 b + 1 \end{cases}$ 解集为3≤x＜5，则 $\frac{b}{a}$ 的值为（）

A、﹣2 B、 $- \frac{1}{2}$ C、﹣4 D、﹣ $\frac{1}{4}$

查看试题解析
8. 如图，点 $A$ 在点 $O$ 的北偏西 $30 °$ 的方向 $5 km$ 处， $AB ⊥ OA .$ 根据已知条件和图上尺规作图的痕迹判断，下列说法正确的是（）

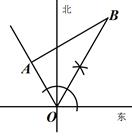A、点 $B$ 在点 $A$ 的北偏东 $30 °$ 方向 $5 km$ 处 B、点 $B$ 在点 $A$ 的北偏东 $60 °$ 方向 $5 km$ 处 C、点 $B$ 在点 $A$ 的北偏东 $30 °$ 方向 $5 \sqrt{3} km$ 处 D、点 $B$ 在点 $A$ 的北偏东 $60 °$ 方向 $5 \sqrt{3} km$ 处

查看试题解析
9. 如图，在等腰Rt△OAA₁中，∠OAA₁=90°，OA=1，以OA₁为直角边作等腰Rt△OA₁A₂ ，以OA₂为直角边作等腰Rt△OA₂A₃ ， …则OA_2n的长度为（）

A、 $2 n$ B、 $2 \sqrt{2} n$ C、 $2^{n}$ D、 $2^{n} \sqrt{2}$

查看试题解析
10. 如图，在平面直角坐标系中，点A是x轴正半轴上的一个动点，点C是y轴正半轴上的点，BC⊥AC于点C．已知AC=16，BC=6．点B到原点的最大距离为（）

A、22 B、18 C、14 D、10

查看试题解析

二、填空题（本大题有6小题，每小题4分，共24分）

11. 写出命题“直角三角形的两个锐角互余”的逆命题：．

查看试题解析
12. 已知 $y$ 与 $x - 2$ 成正比例，且当 $x = 1$ 时， $y = 1$ ，则 $y$ 与 $x$ 之间的函数关系式为．

查看试题解析
13. 已知关于 $x$ 的不等式组 ${\begin{array}{l} 5 - 3 x \geq - 1 ， \\ a - 2 x < 0 \end{array}$ 无解，则 $a$ 的取值范围是．

查看试题解析
14. 一次函数 $y = kx + 2 k - 3$ 的图象经过第一、三、四象限，则 $k$ 的取值范围是．

查看试题解析
15. 如图，已知，直角 $△ ABC$ 中， $∠ ACB = 90 °$ ，从直角三角形两个锐角顶点所引的中线的长 $AD = 5$ ， $BE = \sqrt{55}$ ，则斜边 $AB$ 之长为．

查看试题解析
16. 如图，在平面直角坐标系中，直线 $AB ： y = - x + b$ 交 $y$ 轴于点 $A (0 ， 2)$ ，交 $x$ 轴于点 $B$ ，直线1垂直平分 $OB$ 交 $AB$ 于点 $D$ ，交 $x$ 轴于点 $E$ ，点 $P$ 是直线1上且在第一象限一动点．若 $△ AOP$ 是等腰三角形，点 $P$ 的坐标是．

查看试题解析

三、解答题（本大题有7小题，共66分）

17. 解不等式 $($ 组 $)$
$(1) 3 (x - 1) \leq x + 5$

$(2) {\begin{array}{l} 4 x + 6 > 1 - x ， \\ \frac{4 + 3 x}{6} - \frac{1 + 2 x}{3} \leq 1 \end{array}$

查看试题解析
18. 如图，在平面直角坐标系中， $P (a ， b)$ 是三角形 $ABC$ 的边 $AB$ 上一点，三角形 $ABC$ 经平移后点 $P$ 的对应点为 $P_{1} (a - 2 ， b + 5)$ ．

(1)、请画出经过上述平移后得到的三角形 $A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ ， $C_{1}$ 的坐标；

(2)、求点A₁到B₁C₁的距离．

查看试题解析
19. 已知y是关于x的一次函数，且点(0，4)，(1，2)在此函数图象上．

(1)、求这个一次函数表达式；

(2)、求当-2≤y<4时x的取值范围；

(3)、在函数图象上有点P，点P到y轴的距离为2，直接写出P点的坐标.

查看试题解析
20. 已知：如图，∠B=30°， ∠ACD=45°，AD是BC上的高线，CE是AB边上的中线，DG⊥CE于G.

(1)、若 $AB = 6$ ，求线段AC的长；

(2)、求证： $CG = EG$ .

查看试题解析
21. 某商场销售一种西装和领带，西装每套定价200元，领带每条定价40元.国庆节期间商场决定开展促销活动，活动期间向客户提供两种优惠方案：
方案一：买一套西装送一条领带；

方案二：西装和领带都按定价的90%付款.

现某客户要到该商场购买西装20套，领带x $(x > 20) 条$ .

(1)、若该客户按方案一购买，需付款多少元（用含x的式子表示）？若该客户按方案二购买，需付款多少元（用含x的式子表示）？

(2)、若 $x = 30$ ，通过计算说明此时按哪种方案购买较为合算；

(3)、当 $x = 30$ 时，你能给出一种更为省钱的购买方法吗？试写出你的购买方法和所需费用.

查看试题解析
22. 已知 $△ ABC$ 的高 $AD$ 恰好平分边 $BC$ ，点 $E$ 是线段 $AD$ 上一动点.

(1)、如图1，若 $EA = EC ， ∠ BAC = 50^{o}$ ，求 $∠ AEC$ 的度数为；

(2)、如图2，若 $∠ BAC = 60^{o}$ ， $DE = DC$ ， $AB = 2$ ，求AE的长；

(3)、如图3，若点 $P$ 是 $BA$ 延长线上一点且 $EP = EC$ ， $∠ BAC = α^{o}$ ，求 $∠ APE + ∠ DCE$ 的值.

查看试题解析
23. 已知：如图点 $A (8 ， 6)$ 在正比例函数图象上，点 $B$ 坐标为 $(16 ， 0)$ ，连接 $A B$ ，点 $C$ 是线段 $A B$ 的中点，点 $P$ 在线段 $B O$ 上以每秒 $2$ 个单位的速度由点 $O$ 向点 $B$ 运动，点 $Q$ 在射线 $O A$ 上由点 $O$ 向点 $A$ 运动， $P$ 、 $Q$ 两点同时运动，同时停止，运动时间为 $t$ 秒.

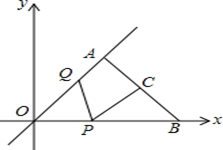(1)、求该正比例函数的解析式：

(2)、当 $t = 2$ 秒，且 $S_{△ O P Q} = 6$ 时，求点 $Q$ 的坐标：

(3)、连接 $C P$ ，在点 $P$ 、 $Q$ 运动过程中， $△ O P Q$ 与 $△ B P C$ 是否全等？如果全等，请求出点 $Q$ 的运动速度；如果不全等，请说明理由

查看试题解析