浙江省温州市瑞安市塘下六校联考2020-2021学年九年级下学期数学入学考试试卷

试卷更新日期：2022-01-06 类型：开学考试

进入出卷网下载

一、单选题

1. 数﹣ $\frac{1}{2}$ ，π ， 3，0中，最大的数是（）

A、﹣ $\frac{1}{2}$ B、π C、3 D、0

查看试题解析
2. 中国倡导的一带一路计划沿线覆盖 $4 400 000 000$ 人口，数据 $4 400 000 000$ 用科学记数法表示为（）

A、 $4.4 \times 10^{9}$ B、 $44 \times 10^{7}$ C、 $0.44 \times 10^{9}$ D、 $440 \times 10^{6}$

查看试题解析
3. 如图，桌面上有两卷圆柱形垃圾袋，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛，而这9名同学只知道自己的成绩，要想让他们知道自己是否入选,老师只需公布他们成绩的（　　）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
5. 如图，点 $D$ 在 $B A$ 的延长线上， $A E ∕ ∕ B C$ .若 $∠ D A C = 100 °$ ， $∠ B = 65 °$ ，则 $∠ E A C$ 的度数为（）

A、 $65 °$ B、 $35 °$ C、 $30 °$ D、 $40 °$

查看试题解析
6. 要使分式 $\frac{x + 1}{x - 1}$ 有意义，则 $x$ 的取值应满足（）

A、 $x = - 1$ B、 $x = 1$ C、 $x \neq 1$ D、 $x \neq - 1$

查看试题解析
7. 如图，在△ABC中，AB＝AC，∠B＝30°，以点A为圆心，以3cm为半径作⊙A.若BC与⊙A相切，则AB的长为（）cm.

A、3 B、3 $\sqrt{3}$ C、6 D、2 $\sqrt{3}$

查看试题解析
8. 如图，是梯子两梯腿张开的示意图，AB＝AC，梯腿与地面夹角∠ACB＝∠ $α$ ，当梯子顶端离地面高度AD＝2.8m时，则梯子两梯脚之间的距离BC＝（）m.

A、 $\frac{14}{5 \tan α}$ B、 $\frac{14 \tan α}{5}$ C、 $\frac{28 \tan α}{5}$ D、 $\frac{28}{5 \tan α}$

查看试题解析
9. 已知（﹣3，y₁），（﹣2，y₂），（1，y₃）是抛物线y＝﹣x²﹣4x＋a上的点，则（）

A、y₃＜y₂＜y₁ B、y₃＜y₁＜y₂ C、y₂＜y₃＜y₁ D、y₁＜y₃＜y₂

查看试题解析
10. 如图：四个形状大小相同的等腰三角形△ABE，△ADF，△CDG，△BCH按如图摆放在正方形ABCD的内部，顺次连接E、F、G、H得到四边形EFGH.若∠AEB＝∠AFD＝∠CGD＝∠BHC＝120°，且EH＝ $\sqrt{6}$ ﹣ $\sqrt{2}$ ，则BC的长为（　　）

A、 $\sqrt{6} + \sqrt{2}$ B、4 $\sqrt{3}$ ﹣4 C、2 $\sqrt{3}$ D、2

查看试题解析

二、填空题

11. 因式分解： $a^{2} + 2 a =$ ．

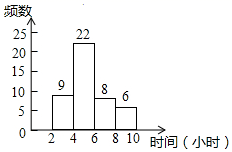
查看试题解析
12. 已知不等式组 ${\begin{array}{l} x - 2 < 0 \\ x + 1 \geq 0 \end{array}$ 的解集为 .

查看试题解析
13. 圆心角为120°，半径为4的扇形的面积是.

查看试题解析
14. 如图是九（1）班45名同学每周课外阅读时间的频数分布直方图（每组含前一个边界值，不含后一个边界值）.其中每周课外阅读时间在6小时及以上的人有名.

查看试题解析
15. 如图，在Rt△ABC中，点D为斜边AC上的一点（不与点A、C重合），BD＝4，过点A，B，D作⊙O，当点C关于直线BD的对称点落在⊙O上时，则⊙O的半径等于.

查看试题解析
16. 如图，在河对岸有一等腰三角形场地EFG，FG＝EG，为了估测场地的大小，在笔直的河岸上依次取点C，D，B，A，使FC⊥l，BG⊥l，EA⊥l，点E，G，D在同一直线上，在D观测F后，发现∠FDC＝∠EDA，测得CD＝12米，DB＝6米，AB＝12米，则FG＝米.

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{25} + {(π - 3)}^{0} - \tan 45^{°}$ .

(2)、化简： ${(x - 2)}^{2} - x (x - 1)$ .

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点D作DE⊥AB于点E.

(1)、求证：△ADC≌△ADE.

(2)、若CD＝2，BD＝4，求BE的长.

查看试题解析
19. 一个不透明的布袋里装有2个红球，1个白球，它们除颜色外其余都相同.

(1)、摸出1个球，记下颜色后不放回，再摸出1个球，求两次摸出的球恰好颜色相同的概率（要求画树状图或列表）.

(2)、现再将 $n$ 个白球放入布袋，搅匀后，使摸出1个球是白球的概率为 $\frac{5}{7}$ ，求 $n$ 的值.

查看试题解析
20. 如图，在6×6正方形网格中，四边形ABCD的顶点均在格点上，请按下列要求作图.

(1)、如图1，在BC上找一格点E，连接AE，DE，使得三角形ADE为直角三角形.

(2)、如图2，F为BC中点，请在网格中找一格点G，作直线FG，使得FG平分四边形ABCD的面积.

查看试题解析
21. 如图，在△ABC中，AB＝AC，以AB为直径的半圆O交BC于点D，交AC于点E，点F为CE的中点，连接DF，DE，AD.

(1)、求证：CD＝DE.

(2)、若OA＝5，sin∠CAB＝ $\frac{4}{5}$ ，求DF的长.

查看试题解析
22. 如图，已知二次函数y＝﹣（x＋1）（x﹣3m）与x轴交于点A，点B（点B在点A的右边），交y轴于点C，其中m＞0.

(1)、直接写出点B，点C的坐标，及抛物线的对称轴.（用m的代数式表示）

(2)、过OB的中点M做x轴垂线交抛物线于点D，交BC于点N，若 $\frac{D N}{N M} = \frac{3}{2}$ ，求m的值.

查看试题解析
23. 小张打算用3600元（全部用完）从商城购进甲、乙两种型号垃圾桶进行零售，进价和零售价如下表所示：

进价（元/个）

零售价（元/个）

甲型号垃圾桶

12

16

乙型号垃圾桶

30

36

设购进甲型号垃圾桶x个，乙型号垃圾桶y个.

(1)、求y关于x的函数表达式.

(2)、若甲、乙型号的垃圾桶的进货总和不超过160个，问小张如何进货，垃圾桶全部卖完后能获得最大的利润.

(3)、小张为了吸引更多的客源，决定调整甲型号垃圾桶零售价. 若每个甲型号垃圾桶零售价降价a元，甲、乙型号垃圾桶全部售完，小张发现获得的利润为常数，与 $x ， y$ 均无关，求a的值.

查看试题解析
24. 矩形ABCD中，AF、CE分别平分∠BAD，∠BCD，并交线段BC，AD于点F，E.当动点P从点A匀速运动到点F时，动点Q恰好从点C匀速运动到点B.记AP＝x，BQ＝y，且y与x满足关系式：y＝﹣ $\frac{5 \sqrt{2}}{4}$ x＋10.

(1)、判断AF与CE的位置关系，并说明理由.

(2)、求AF，CF的长度.

(3)、①当PQ平行于△ECD的一边时，求所有满足条件的x的值.
②连接DB，对角线DB交PQ于点O，若点O恰好为PQ的三等分点，请直接写出x的值.

查看试题解析

	进价（元/个）	零售价（元/个）
甲型号垃圾桶	12	16
乙型号垃圾桶	30	36