浙江省宁波市余姚市2021-2022学年九年级上学期第二次月考数学试卷

试卷更新日期：2022-01-06 类型：月考试卷

进入出卷网下载

一、选择题（每小题4分，共40分，在每小题给出的四个选项中，只有一项符合题目要求）

1. 若 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{5}{3}$ C、 $\frac{3}{5}$ D、 $\frac{3}{2}$

查看试题解析
2. 如图，正方形ABCD内接于⊙O，点P在 $\overset{⌢}{A B}$ 上，则∠BPC的度数为（　　）

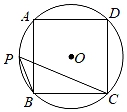A、30° B、45° C、60° D、90°

查看试题解析
3. 将二次函数y＝（x﹣1）²+2的图象先向右移动2个单位，向下平移3个单位，得到的图象对应的表达式是（　　）

A、y＝（x+2）²+4 B、y＝（x﹣3）²﹣1 C、y＝（x﹣3）²+5 D、y＝（x+1）²+5

查看试题解析
4. 在正面完全相同、反面印有下列四个图形的纸片中，任抽一张，则抽到的图形中，既是轴对称图形，又是中心对称图形的概率是（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
5. 如图，点A，B，C在⊙O上，∠B＝120°，则∠AOC的度数为（　　）

A、120° B、110° C、130° D、125°

查看试题解析
6. 二次函数y＝ax²+bx+c（a≠0）的图象如图所示，下列说法中，错误的是（　　）

A、对称轴是直线x＝ $\frac{1}{2}$ B、当﹣1＜x＜2时，y＜0 C、a+c＝b D、a+b＞﹣c

查看试题解析
7. 如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为6，则阴影部分的面积为（　　）

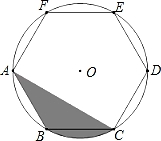A、12π B、6π C、9π D、18π

查看试题解析
8. 二次函数y＝﹣x²+2x+4，当﹣1≤x≤2时，则（）

A、1≤y≤4 B、y≤5 C、4≤y≤5 D、1≤y≤5

查看试题解析
9. 如图，△ABC中，AB＝10，AC＝8，BC＝4，以点A为圆心，AB为半径作圆，交BC的延长线于点D，则CD长为（　　）

A、10 B、9 C、4 $\sqrt{5}$ D、8

查看试题解析
10. 如图，在Rt△ABC中，∠ACB＝90°，以该三角形的三条边为边向外作正方形，正方形的顶点E，F，G，H，M，N都在同一个圆上.记该圆面积为S₁ ， △ABC面积为S₂ ，则 $\frac{S_{1}}{S_{2}}$ 的值是（　　）

A、 $\frac{5 π}{2}$ B、3π C、5π D、 $\frac{11 π}{2}$

查看试题解析

二、填空题（每小题5分，共30分）

11. 抛物线y＝﹣2x²+4x﹣3的对称轴是.

查看试题解析
12. 已知弧的长为3πcm，弧的半径为6cm，则圆弧的度数为.

查看试题解析
13. 点C是线段AB的黄金分割点（AC＞BC），AB＝2，则AC＝.（用根号表示）

查看试题解析

14. 若二次函数：y＝ax²+bx+c的x与y的部分对应值如表，则a+b+c＝.

x	﹣7	﹣6	﹣5	﹣4	﹣3	﹣2
y	﹣27	﹣13	﹣3	3	5	3

查看试题解析

15. 已知⊙O半径为1，AB是⊙O的一条弦，且AB＝ $\sqrt{2}$ ，则弦AB所对的圆周角度数是°.

查看试题解析
16. 如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是.

查看试题解析

三、解答题（第17～19题各8分，第20～22题各10分，第23题12分，第24题14分，共80分）

17. 已知线段a、b满足a：b＝3：2，且a+2b＝28.

(1)、求a、b的值.

(2)、若线段x是线段a、b的比例中项，求x的值.

查看试题解析
18. 在平面直角坐标系中，点A的坐标是（0，3），点B在x轴上，将△AOB绕点A逆时针旋转90°得到△AEF，点O、B的对应点分别是点E、F.

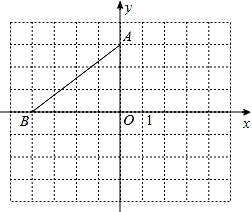(1)、若点B的坐标是（﹣4，0），请在图中画出△AEF，并写出点E、F的坐标.

(2)、当点F落在x轴的上方时，试写出一个符合条件的点B的坐标.

查看试题解析
19. 已知抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c经过点（1，0），（0， $\frac{3}{2}$ ）.

(1)、求该抛物线的函数表达式；

(2)、将抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c平移，使其顶点恰好落在原点，请写出一种平移的方法及平移后的函数表达式.

查看试题解析
20. 2018年6月，宁波全面推进生活垃圾分类工作，如图是某小区放置的垃圾桶，从左到右依次是红色：有害垃圾；蓝色：可回收垃圾；绿色：厨余垃圾；黑色：其他垃圾.

(1)、居民A将一袋厨余垃圾随手放入一个垃圾桶，问他能正确投放垃圾的概率是.

(2)、居民B手拎两袋垃圾，一袋是可回收垃圾，另一袋是有害垃圾，她先将可回收垃圾随手放入一个垃圾桶，然后把另一袋垃圾又随手放入其他垃圾桶.问：两袋垃圾都投放错误的概率？请画出树状图或列表说明理由.

查看试题解析
21. 如图，已知△ABC内接于⊙O，点D是 $\overset{⌢}{B C}$ 的中点，连接OD，交BC于点E.

(1)、如图1，当圆心O在AB边上时，求证：OD∥AC；

(2)、如图2，当圆心O在△ABC外部时，连接AD和CD，若∠BAC＝36°， $\overset{⌢}{A C}$ 的度数是88°，求∠ACD的度数；

(3)、如图3，当圆心O在△ABC内部时，连接BD和CD，若∠ABC＝45°，DE＝2，BC＝4 $\sqrt{3}$ ，求四边形ACDB的面积.

查看试题解析
22. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为y＝﹣ $\frac{1}{6}$ （x﹣5）²+6.

(1)、求雕塑高OA.

(2)、求落水点C，D之间的距离.

(3)、若需要在OD上的点E处竖立雕塑EF，OE＝10m，EF＝1.8m，EF⊥OD.问：顶部F是否会碰到水柱？请通过计算说明.

查看试题解析
23. 如图，在平面直角坐标系中，已知抛物线y＝x²+bx+c与直线AB相交于A，B两点，其中A（﹣3，﹣4），B（0，﹣1）.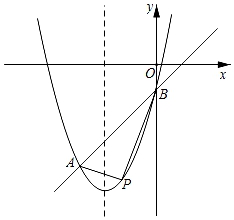

(1)、求该抛物线的函数表达式.

(2)、点P为直线AB下方抛物线上的任意一点，连接PA，PB，求△PAB面积的最大值.

(3)、在二次函数的对称轴上找一点C，使得△ABC是等腰三角形，求满足条件的点C的坐标.

查看试题解析
24. 定义：若两个三角形有一对公共边，且另有一组对应边和一对对应角分别对应相等，那么这两个三角形称为邻等三角形.
例如：如图1，△ABC中，AD＝AD，AB＝AC，∠B＝∠C，则△ABD与△ACD是邻等三角形.

(1)、如图2，⊙O中，点D是 $\overset{⌢}{B C}$ 的中点，那么请判断△ABD与△ACD是否为邻等三角形，并说明理由.

(2)、如图3，以点A（2，2）为圆心，OA为半径的⊙A交x轴于点B（4，0），△OBC是⊙A的内接三角形，∠COB＝30°.
①求∠C的度数和OC的长；
②点P在⊙A上，若△OCP与△OBC是邻等三角形时，请直接写出点P的坐标.

查看试题解析