浙江省杭州市余杭区2021-2022学年八年级上学期12月月考数学试卷
试卷更新日期:2022-01-06 类型:月考试卷
一、选择题:本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项最符合题目要求。
-
1. 下列各点,在第一象限的是A、 B、 C、 D、2. 下面各组线段中,能组成三角形的是( )A、5,11,6 B、8,8,16 C、10,5,4 D、6,9,143. 下列选项正确的是A、不是负数,表示为 B、不大于3,表示为 C、与4的差是负数,表示为 D、不等于 , 表示为4. 在数轴上表示不等式的解集正确的是A、
 B、
B、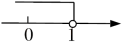 C、
C、 D、
D、 5. 有下列条件:①;②;③;④ , 其中能确定是直角三角形的是A、①②④ B、①②③ C、①③④ D、②③④6. 已知关于的不等式的解集为 , 则的取值范围是A、 B、 C、 D、7. 一辆汽车从甲地以的速度驶往乙地,已知甲地与乙地相距 , 则汽车距乙地的距离与行驶时间之间的函数解析式是A、 B、 C、 D、8. 如图,已知 , 是两条相交线段,连结 , , 分别作和的平分线相交于点 , 若 , , 则的度数为
5. 有下列条件:①;②;③;④ , 其中能确定是直角三角形的是A、①②④ B、①②③ C、①③④ D、②③④6. 已知关于的不等式的解集为 , 则的取值范围是A、 B、 C、 D、7. 一辆汽车从甲地以的速度驶往乙地,已知甲地与乙地相距 , 则汽车距乙地的距离与行驶时间之间的函数解析式是A、 B、 C、 D、8. 如图,已知 , 是两条相交线段,连结 , , 分别作和的平分线相交于点 , 若 , , 则的度数为 A、 B、 C、 D、9. 如图,将一个等腰直角三角形按如图所示的方式翻折,若折痕的长度为 , 有下列结论:①平分;②的长为;③是等腰三角形;④的周长等于的长.其中说法正确的是
A、 B、 C、 D、9. 如图,将一个等腰直角三角形按如图所示的方式翻折,若折痕的长度为 , 有下列结论:①平分;②的长为;③是等腰三角形;④的周长等于的长.其中说法正确的是 A、①②③ B、②④ C、②③④ D、③④10. 如图所示,点为内一定点,点 , 分别在的两边上,若的周长最小,则与的关系为
A、①②③ B、②④ C、②③④ D、③④10. 如图所示,点为内一定点,点 , 分别在的两边上,若的周长最小,则与的关系为 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题有6个小题,每小题4分,共24分。
-
11. 点关于轴的对称点是.12. 如果用总长为的篱笆围成一个长方形场地,设长方形的面积为 , 周长为 , 一边长为 , 那么在 , , 中是变量的是.13. 已知中, , 平分 , 平分 , 若 , 则的度数为.14. 已知点 , , 若轴,且线段 , 则 , .15. 一根蜡烛长 , 点燃后每小时燃烧 , 燃烧时剩下的高度(单位:cm)与燃烧时间(单位:h)之间的关系是.
16. 比较大小,用“”或“”填空:(1)、若 , 且 , 则.(2)、若 , 为实数,则.三、解答题:本题有7小题,共66分。解答应写出文字说明、证明过程或演算步骤。
-
17. 如图,已知线段 , .
 (1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.18. 解下列不等式:(1)、;(2)、.19. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.
(1)、尺规作图:作等腰 , 使底边长为 , 上的高为.(2)、若 , , 求的周长.18. 解下列不等式:(1)、;(2)、.19. 如图,在中, , , 是边上的点,且 , 过点作边的垂线交边于点 , 求的长.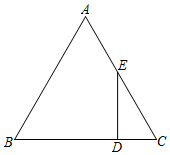 20. 已知等腰三角形的周长为12,设腰长为 , 底边长为.(1)、试写出关于的函数解析式,并直接写出自变量的取值范围;(2)、当时,求出函数值.21. 经销商销售甲型、乙型两种产品,价格随销售量的变化而不同,具体如表:
20. 已知等腰三角形的周长为12,设腰长为 , 底边长为.(1)、试写出关于的函数解析式,并直接写出自变量的取值范围;(2)、当时,求出函数值.21. 经销商销售甲型、乙型两种产品,价格随销售量的变化而不同,具体如表:销售量(件
价格(元件)
型号
甲型
乙型
已知销售10件甲型产品和30件乙型产品的销售额为750元;销售60件甲型产品和100件乙型产品的销售额为2520元.
(1)、求、的值;(2)、若学校要购买甲型、乙型两种产品共101件,购买的甲产品少于乙产品,所用经费不超过1680元,则有多少种购买方案?

