浙教版备考2022年中考数学一轮复习专题9 一元二次方程及其应用

试卷更新日期：2022-01-06 类型：一轮复习

进入出卷网下载

一、单选题

1. 若方程（a﹣3）x²＋x＋a＝0是关于x的一元二次方程，则（）

A、a≠0 B、a≠3 C、a＞0 D、a＞3

查看试题解析
2. 已知方程x²＋mx＋3＝0的一个根是1，则方程另一个根是（）

A、x＝－4 B、x＝－3 C、x＝3 D、x＝4

查看试题解析
3. 已知关于x的一元二次方程 $x^{2} + 2 x - 1 = 0$ ，则下列关于该方程根的判断，正确的是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、不能确定

查看试题解析
4. 方程2x²+x＝3的二次项系数、一次项系数、常数项分别是（　　）

A、2，0，3 B、2，1，3 C、2，0，﹣3 D、2，1，﹣3

查看试题解析
5. 已知二次函数y＝x²－bx+c的图象经过A（1，n），B（3，n），且与x轴只有一个交点，则n的值为（）．

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
6. 若关于x的一元二次方程 $(m - 3) x^{2} + 3 x + 1 = 0$ 有实数根，则m的取值范围中，正整数值有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 将一元二次方程 $x^{2} + 4 x - 1 = 0$ 化成 ${(x - a)}^{2} = b$ （a，b为常数）的形式，a，b的值分别为（）

A、 $a = 2 ， b = 3$ B、 $a = 2 ， b = 5$ C、 $a = - 2 ， b = 3$ D、 $a = - 2 ， b = 5$

查看试题解析
8. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，配方结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ， $a ， b ， c$ 为常数）中，函数y与自变量x的部分对应值如下表，则方程 $a x^{2} + b x + c = 0$ 的一个解的范围是（）

$x$

3. 17

3.18

3.19

$y$

$- 0.03$

$- 0.01$

0.02

A、 $- 0.03 < x < - 0.01$ B、 $3.18 < x < 3.19$ C、 $- 0.01 < x < 0.02$ D、 $3.17 < x < 3.18$

查看试题解析
10. 某商品经过连续两次降价，每件售价由原来的144元降到了121元，设平均每次降价的百分率为x，则可列方程为（）

A、144（1﹣x）²＝121 B、144（1+x）²＝121 C、（1﹣x）²＝121 D、121（1+x）²＝144

查看试题解析

二、填空题

11. 如图，已知二次函数y＝ax²+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝1.下列结论：①abc＞0；②4a+2b+c＞0；③4ac﹣b²＞8a；④ $\frac{1}{3}$ ＜a＜ $\frac{2}{3}$ .其中正确的选项是.（填序号）

查看试题解析
12. 如图，在等边三角形ABC中，D是AC的中点，P是边AB上的一个动点，过点P作PE⊥AB，交BC于点E，连接DP，DE.若AB＝8，△PDE是等腰三角形，则BP的长是.

查看试题解析
13. 已知关于x的方程 $| x^{2} + 2 p x - 3 p^{2} + 5 | - q = 0$ ，其中p、q都是实数.若方程有三个不同的实数根 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ ，且 $\frac{1}{x_{1}} + \frac{1}{x_{2}} + \frac{1}{x_{3}} = 0$ ，则q的值为.

查看试题解析
14. 在平面直角坐标系中点A（0，6）、B（6，0），AC、BD分别垂直于y轴、x轴，CA＝3，∠COD＝45°，二次函数y＝﹣ $\frac{1}{8}$ x²+m与线段CD有两个公共点时，m的取值范围是.

查看试题解析
15. 若关于x的方程(a+1)x²+(2a﹣3)x+a﹣2＝0有两个不相等的实根，且关于x的方程 $\frac{a x}{1 + x} - 1 = \frac{3}{x + 1}$ 的解为整数，则满足条件的所有整数a的和是．

查看试题解析
16. 如图，直线y＝﹣x＋m与双曲线y＝﹣ $\frac{2}{x}$ 相交于A，B两点BC∥x轴，AC∥y轴，则△ABC面积的最小值为.

查看试题解析

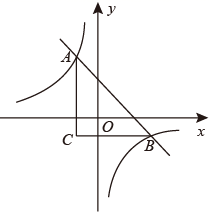
三、综合题

17. 受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素，我市某汽车零部件生产企业的利润逐年提高，据统计，2016年利润为3亿元，2018年利润为4.32亿元．

(1)、求该企业从2016年到2018年利润的年平均增长率；

(2)、若2019年保持前两年利润的年平均增长率不变，该企业2019年的利润能否超过5亿元？

查看试题解析
18. 有一个长、宽之比为5 ： 2的长方形过道，其面积为10 m² ．

(1)、求这个长方形过道的长和宽；

(2)、用40块大小一样的正方形地板砖刚好把这个过道铺满，求这种地板砖的边长．

查看试题解析
19. 某果商按每千克10元的价格收购了1000千克精品红富士苹果存入冷库中，预测这种苹果的市场价格平均每天每千克上涨0.5元，但冷库存放这批苹果时每天需要支出各种费用合计110元，同时，平均每天有3千克的苹果腐烂不能出售，而且这种苹果在冷库中最多能保存90天．

(1)、若该果商将这批苹果存放x天后一次性出售，则x天后这批苹果的销售单价为（）元，销售量为（）千克（用含x的代数式表示）；

(2)、这次销售后该果商共获得利润12000元，求这批苹果存放了多少天后出售？

查看试题解析
20.

(1)、用配方法解方程： $x^{2} - 2 x - 8 = 0$ ；

(2)、若关于x的一元二次方程 $(k - 1) x^{2} + 3 x + k^{2} - 1 = 0$ 有一个解为 $x = 0$ ，求k的值．

查看试题解析
21. 已知关于x的方程x²+2x+a＝0．

(1)、若该方程有两个不相等的实数根，求实数a的取值范围．

(2)、当该方程的一个根为1时，求a的值及方程的另一根．

查看试题解析
22. 如图，在Rt△ABC中，∠C＝90°，AC=10cm，BC＝8cm．点M从点C出发，以2cm/s的速度沿CA向点A匀速运动，点N从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一点也随即停止运动．

(1)、经过几秒后，△MCN的面积等于△ABC面积的 $\frac{2}{5}$ ？

(2)、经过几秒，△MCN与△ABC相似？

查看试题解析
23. 某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销．经过调查，每天销售量 $y$ （件）与销售单价 $x$ （元/件）满足一次函数关系，其部分对应数据如表．

销售单价 $x$ （元/件）

…

20

30

40

…

每天销售量 $y$ （件）

…

500

400

300

…

(1)、把表中 $x$ 、 $y$ 的各组对应值作为点的坐标，求出函数关系式；

(2)、相关物价部门规定，该工艺品销售单价最高不能超过35元/件，当销售单价定为多少时，工艺厂试销该工艺品每天获得的利润为8000元？

查看试题解析
24. 数学教科书中这样写道：“我们把多项式a²+2ab+b²及a²﹣2ab+b²叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：
先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．

例如：分解因式x²+2x﹣3＝（x²+2x+1）﹣4＝（x+1）²﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）；例如求代数式2x²+4x﹣6的最小值，2x²+4x﹣6＝2（x²+2x﹣3）＝2（x+1）²﹣8，可知当x＝﹣1时，2x²+4x﹣6有最小值，最小值是﹣8．

根据阅读材料用配方法解决下列问题：

(1)、分解因式：m²﹣4m﹣5＝．

(2)、求代数式x²+2x+4的最小值．

(3)、已知a、b、c是△ABC的三边长，且满足a²+c²+2b（b﹣a﹣c）＝0，试判断△ABC的形状．

查看试题解析
25. 请阅读下列材料，并按要求完成相应的任务：
人类对一元二次方程的研究经历了漫长的岁月．一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中．到了中世纪，阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法，并用几何法进行了证明．我国古代三国时期的数学家赵爽也给出了类似的几何解法．赵爽在其所著的《勾股圆方图注》中记载了解方程 $x^{2} + 5 x -14 = 0$ 即 $x (x + 5) = 14$ 得方法.首先构造了如图1所示得图形，图中的大正方形面积是 ${(x + x + 5)}^{2}$ ，其中四个全等的小矩形面积分别为 $x (x + 5) = 14$ ，中间的小正方形面积为 $5^{2}$ ，所以大正方形的面积又可表示为 $4 \times 14 + 5^{2}$ ，据此易得 $x = 2$ ．

　　　　　

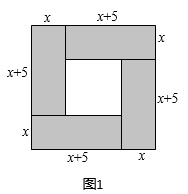
任务：

(1)、参照上述图解一元二次方程的方法，请在下面三个构图中选择能够说明方程 $x^{2} -4 x -12 = 0$ 的正确构图是（从序号①②③中选择）．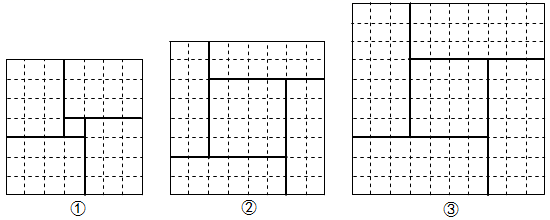

(2)、请你通过上述问题的学习，在图2的网格中设计正确的构图，用几何法求解方程 $x^{2} + 2 x -15 = 0$ （写出必要的思考过程）．

查看试题解析
26. 观察下列分解因式的过程：x²＋2xy－3y²
解：原式＝x²＋2xy＋y²－y²－3y²

＝(x²＋2xy＋y²)－4y²

＝(x＋y)²－(2y)²

＝(x＋y＋2y)(x＋y－2y)

＝(x＋3y)(x－y)

像这种通过增减项把多项式转化成完全平方形式的方法称为配方法.

(1)、请你运用上述配方法分解因式：x²＋4xy－5y²

(2)、代数式x²＋2x＋y²－6y＋15是否存在最小值？如果存在，请求出当x、y分别是多少时，此代数式存在最小值，最小值是多少？如果不存在，请说明理由.

(3)、求-x²-8x+15的最大值，并写出相应的x的值.

查看试题解析
27. 阅读材料：各类方程的解法不尽相同，但是它们有一个共同的基本数学思想——转化，把未知转化为已知．用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程 $x^{3} - 2 x^{2} - 3 x = 0$ ，通过因式分解可以把它转化为 $x (x^{2} - 2 x - 3) = 0$ ，解方程 $x = 0$ 和 $x^{2} - 2 x - 3 = 0$ ，可得方程 $x^{3} - 2 x^{2} - 3 x = 0$ 的解．
问题：

(1)、方程 $x^{3} - 2 x^{2} - 3 x = 0$ 的解是 $x_{1} = 0$ ， $x_{2} =$ ， $x_{3} =$ ．

(2)、求方程 $x^{3} = 6 x^{2} + 16 x$ 的解．

(3)、用“转化”思想求方程 $\sqrt{- 2 x + 15} = x$ 的解．

查看试题解析
28. 阅读材料：
材料1 若一元二次方程ax²+bx+c＝0（a≠0）的两个根为x₁ ， x₂则x₁+x₂＝﹣ $\frac{b}{a}$ ，x₁x₂＝ $\frac{c}{a}$ .

材料2 已知实数m，n满足m²﹣m﹣1＝0，n²﹣n﹣1＝0，且m≠n，求 $\frac{n}{m} + \frac{m}{n}$ 的值.

解：由题知m，n是方程x²﹣x﹣1＝0的两个不相等的实数根，根据材料1得m+n＝1，mn＝﹣1，所以 $\frac{n}{m} + \frac{m}{n} = \frac{m^{2} + n^{2}}{m n} = \frac{{(m + n)}^{2} - 2 m n}{m n} = \frac{1 + 2}{- 1}$ ＝﹣3.

根据上述材料解决以下问题：

(1)、材料理解：一元二次方程5x²+10x﹣1＝0的两个根为x₁ ， x₂ ，则x₁+x₂＝， x₁x₂＝.

(2)、类比探究：已知实数m，n满足7m²﹣7m﹣1＝0，7n²﹣7n﹣1＝0，且m≠n，求m²n+mn²的值：

(3)、思维拓展：已知实数s、t分别满足19s²+99s+1＝0，t²+99t+19＝0，且st≠1.求 $\frac{s t + 4 s + 1}{t}$ 的值.

查看试题解析
29. 阅读下面材料，并完成问题.
任意给定一个矩形A，若存在另一个矩形B，使它的周长和面积分别是矩形A的一半，则称矩形 $A, B$ 是“兄弟矩形”.

探究：当矩形A的边长分别为7和1时，是否存在A的“兄弟矩形”B？

小亮同学是这样探究的：

设所求矩形的两边分别是x和y，由题意，得 ${\begin{array}{l} x + y = 4 ① \\ x y = \frac{7}{2} ② \end{array}$

由①，得 $y = 4 - x$ ，③

把③代入②，得 $x (4 - x) = \frac{7}{2}$ ，

整理，得 $2 x^{2} - 8 x + 7 = 0$ .

$∵ b^{2} - 4 a c = 64 - 56 = 8 > 0$ ，

$∴ A$ 的“兄弟矩形”B存在.

(1)、若已知矩形A的边长分别为3和2，请你根据小亮的探究方法，说明A的“兄弟矩形”B是否存在？

(2)、若矩形A的边长为m和n，当A的“兄弟矩形”B存在时，求 $m, n$ 应满足的条件.

查看试题解析

销售单价 $x$ （元/件）	…	20	30	40	…
每天销售量 $y$ （件）	…	500	400	300	…

$x$	3. 17	3.18	3.19
$y$	$- 0.03$	$- 0.01$	0.02