浙教版备考2022年中考数学一轮复习专题8 一元一次不等式（组）及其应用

试卷更新日期：2022-01-06 类型：一轮复习

进入出卷网下载

一、单选题

1. 不等式3x+4 $\geq$ 1的解集是（）

A、 B、 C、 D、

查看试题解析
2. 随着科技的进步，我们可以通过手机APP实时查看公交车到站情况.小明想乘公交车，可又不想静静地等在A站.他从A站往B站走了一段路，拿出手机查看了公交车到站情况，发现他与公交车的距离为720m（如图），此时有两种选择：（1）与公交车相向而行，到A公交站去乘车；（2）与公交车同向而行，到B公交站去乘车.假设小明的速度是公交车速度的 $\frac{1}{5}$ ，若要保证小明不会错过这辆公交车，则A，B两公交站之间的距离最大为（）

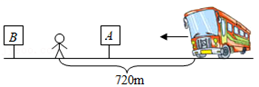A、240m B、300m C、320m D、360m

查看试题解析
3. 若x＜y成立，则下列不等式一定成立的是（）

A、4x＜3y B、﹣2x＜﹣2y C、x²＜y² D、x﹣2018＜y﹣2018

查看试题解析
4. 若x+2022>y+2022，则（）

A、x+2<y+2 B、x－2<y－2 C、－2x<－2y D、2x<2y

查看试题解析
5. 不等式1－x≥x－1的解是（）

A、x≥1 B、x≥－1 C、x≤1 D、x≤－1

查看试题解析
6. 已知点 $P (a ， 2 - a)$ 关于原点对称的点在第四象限，则 $a$ 的取值范围在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 能说明“若x $>$ y，则ax $>$ ay”是假命题的a的值是（）

A、3 B、2 C、1 D、-1

查看试题解析
8. 实数a，b，c在数轴上的对应点的位置如图所示，若|a|>|b|，则下列结论中一定成立的是（）

A、b+c>0 B、a+c<-2 C、 $\frac{b}{a}$ <1 D、abc≥0

查看试题解析
9. 若 $- 1 < a < 0$ ，则 $a ， \frac{1}{a} ， a^{2}$ 由小到大排列正确的是（）

A、 $a^{2} < a < \frac{1}{a}$ B、 $a < \frac{1}{a} < a^{2}$ C、 $\frac{1}{a} < a < a^{2}$ D、 $a < a^{2} < \frac{1}{a}$

查看试题解析
10. 已知某程序如图所示，规定：从“输入实数x”到“结果是否大于95”为一次操作，如果该程序进行了两次操作停止，那么实数x的取值范围是 $($ $)$

A、 $x > 23$ B、 $11 \leq x \leq 23$ C、 $23 < x \leq 47$ D、 $x \leq 47$

查看试题解析

二、填空题

11. 若关于x的不等式组 ${\begin{array}{l} x - m < 0 \\ 7 - 2 x \leq - 1 \end{array}$ 只有3个正整数解，则m的取值范围为.

查看试题解析
12. 经历了漫长艰难的体训，初三学子即将迎来中考体考，初三某班的家长为孩子们准备了脉动饮料、士力架和葡萄糖口服液.已知脉动饮料、士力架和葡萄糖口服液的单价之和为22元，计划购买脉动饮料、士力架和葡萄糖口服液的数量总共不超过200，其中葡萄糖口服液的单价为10元，计划购买50支.脉动饮料的数量不多于士力架数量的一半，但至少购买30瓶.在做预算时，将脉动饮料和士力架的单价弄反了，结果在实际购买时，总费用比预算多了160元.若脉动饮料、士力架和葡萄糖口服液的单价均为整数，则实际购买脉动饮料、士力架和葡萄糖口服液的总费用最多需要花费元.

查看试题解析
13. 已知有甲、乙两个长方形，它们的边长如图所示（m为正整数），面积分别为S₁、S₂。

(1)、请比较S₁与S₂的大小：S₁S₂；

(2)、满足条件4< n < ∣S₁-S₂∣的整数n有且只有4个，则m=

查看试题解析
14. 我国过年历史悠久，在传承发展中己形成了一些较为固定的习俗，有许多还相传至今，如买年货、扫尘、贴对联、吃年夜饭、守岁、拜岁、拜年、舞龙舞狮、拜神祭祖、祈福攘灾、游神、押舟、庙会、游锣鼓、游标旗、上灯酒、赏花灯等.某商店新进一批“福”字贴画和数对灯笼（灯笼一对为2件），共超过250件但不超过300件，灯笼的对数正好是“福”字贴画数量的 $\frac{1}{5}$ ，每张“福”字贴画进价是4元，每对灯笼的进价是50元（灯笼成对出售），商店将“福”字贴画以高出进价的 $\frac{3}{4}$ 售出，将灯笼每对按高出进价的40%售出，最后留下了35件物品未卖出，并把这批物品免费送给了自己的亲戚朋友，最后商店经过计算总利润率为20%，则最初购进灯笼对.

查看试题解析
15. 甲，乙，丙三人做一个抽牌游戏，三张纸牌上分别写有个数字0，x，y（x，y均为正整数，且x＜y），每人抽一张纸牌，纸牌上的数字就是这一轮的得分.经过若干轮后（至少四轮），甲的总得分为20，乙的总得分为10，丙的总得分为9.则甲抽到x的次数最多为.

查看试题解析
16. 12月是成都奶油巧克力草莓大丰收的季节，重庆渝北海领开展“水果一带一路”活动，成都顺丰快递公司出动所有车辆分12月25，26日两批往重庆运输现摘草莓.该公司共有A，B，C三种车型，其中A型车数量占公司车辆总数的一半，B型车数量与C型车数量相等.25日安排A型车数量的一半，B型车数量的 $\frac{1}{3}$ ，C型车数量的 $\frac{3}{4}$ 进行运输，且25日A，B，C三种车型每辆车载货量分别为10吨，15吨，20吨，则25日刚好运完所有草莓重量的一半.26日安排剩下的所有车辆完成剩下的所有草莓的运输，且26日A，B，C三种车型每辆载货量分别不超过14吨，27吨，24吨.26日B型车实际载货量为26日A型车每辆实际载货量的 $\frac{3}{2}$ .已知同型货车每辆的实际载货量相等，A，B，C三种车型每辆车26日运输成本分别为100元/吨，200元/吨，75元/吨，则26日运输时，一辆A型车、一辆B型车，一辆C型车总的运输成本至多为元.

查看试题解析

三、综合题

17. 为全面改善公园环境，现招标建设某全长960米绿化带，A ， B两个工程队的竞标，A队平均每天绿化长度是B队的2倍，若由一个工程队单独完成绿装化，B队比A队要多用6天．

(1)、分别求出A ， B两队平均每天绿化长度．

(2)、若决定由两个工程队共同合作绿化，要求至多4天完成绿化任务，两队都按（1）中的工作效率绿化完2天时，现又多出180米需要绿化，为了不超过4天时限，两队决定从第3天开始，各自都提高工作效率，且A队平均每天绿化长度仍是B队的2倍，则B队提高工作效率后平均每天至少绿化多少米？

查看试题解析
18. 解答下列各题：

(1)、计算： $\frac{1}{a - 1} + \frac{2}{1 - a^{2}}$ ；

(2)、先化简，再求值： $\frac{x^{2} - 4 x + 4}{x + 1} \div (\frac{3}{x + 1} - x + 1)$ ，请从不等式组 ${\begin{array}{l} 5 - 2 x \geq 1 \\ x + 2 \geq 0 \end{array}$ 的整数解中选择一个合适的值代入求值．

查看试题解析
19. 茶为国饮，茶文化是中国传统文化的重要组成部分，这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展，在“春季茶叶节”期间，某茶具店老板购进了A、B两种不同的茶具．若购进A种茶具1套和B种茶具2套，需要250元：若购进A种茶具3套和B种茶具4套需要600元．

(1)、A、B两种茶具每套进价分别为多少元？

(2)、由于茶具畅销，茶具店老板决定再次购进A、B两种茶具共80套茶具厂对这两种类型的茶具进行了价格调整，A种茶具的进价比第一次购进时提高了8%，B种茶具的进价按第一次购进时进价的八折．如果茶具店老板此次用于购进A、B两种茶具的总费用不超过6240元，则茶具店老板最多能购进A种茶具多少套？

查看试题解析
20. 为了弘扬我国书法艺术，培养学生良好的书写能力．某校举办了书法比赛，学校准备为获奖同学颁奖，在购买奖品时发现， $A$ 种奖品的单价比 $B$ 种奖品的单价多10元，用300元购买 $A$ 种奖品的件数与用240元购买 $B$ 种奖品的件数相同．

(1)、求 $A$ ， $B$ 两种奖品的单价各是多少元；

(2)、学校为获奖的15名学生购买奖品（每人一件 $A$ 种奖品或一件 $B$ 种奖品），且购买的总费用不超过700元，求最多可以购买多少件 $A$ 种奖品？

查看试题解析
21. 疫情期间，学校按照防疫要求，学生在进校时必须排队接受体温检测.某校统计了学生早晨到校情况，发现学生到校的累计人数 $y$ （单位：人）随时间 $x$ （单位：分钟）的变化情况如图所示，当 $0 \leq x \leq 10$ 时， $y$ 可看作是 $x$ 的二次函数，其图象经过原点，且顶点坐标为 $(10 ， 500)$ ；当 $10 < x \leq 12$ 时，累计人数保持不变.

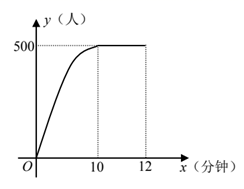(1)、求 $y$ 与 $x$ 之间的函数表达式；

(2)、如果学生一进校就开始测量体温，校门口有2个体温检测棚，每个检测点每分钟可检测20人.校门口排队等待体温检测的学生人数最多时有多少人？全部学生都完成体温检测需要多少时间？

(3)、在（2）的条件下，如果要在8分钟内让全部学生完成体温检测，从一开始就应该至少增加几个检测点？

查看试题解析
22. 定义：对任意一个两位数a，如果a满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“湘一数”.将一个“湘一数”的个位数字与十位数字对调后得到一个新的两位数，把这个两位数与原两位数的和与11的商记为 $f (a)$ .例如：a=23，对调个位数字与十位数字得到新两位数32，新两位数与原两位数的和为23+32=55，和与11的商为55÷11=5，所以 $f (23) = 5$ .
根据以上定义，回答下列问题：

(1)、填空：①下列两位数：50、42，33中，“湘一数”为；②计算： $f (45) =$ .

(2)、如果一个“湘一数”b的十位数字是k，个位数字是 $2 (k + 1)$ ，且 $f (b) = 8$ ，请求出“湘一数”b；

(3)、如果一个“湘一数”c，满足 $c - 5 f (c) > 30$ ，求满足条件的c的值.

查看试题解析
23. 对实数x、y，我们定义一种新运算：F（x，y） $= a x + b y$ （其中a，b为常数）.例如：F（2，3） $= 2 a + 3 b$ ，F（2， $- 3$ ） $= 2 a - 3 b$ .已知F（1，1）=2，F（1， $- 1$ ）=0.

(1)、则 $a =$ ， $b =$ ；

(2)、若方程组 ${\begin{array}{l} F (x ， - y) = 4 m - 3 \\ F (x ， 2 y) = - 5 m \end{array}$ 的解中，x是非正数，y是负数：
①求m的取值范围；

②若 $2^{x} \cdot 4^{y} = 2^{n}$ ，求n的最小值；

(3)、若关于x的不等式组 ${\begin{array}{l} F (3 x ， 0) > - 2 c \\ F (- 2 x ， 0) \geq - 3 c \end{array}$ 恰好有3个整数解，求c的取值范围.

查看试题解析
24.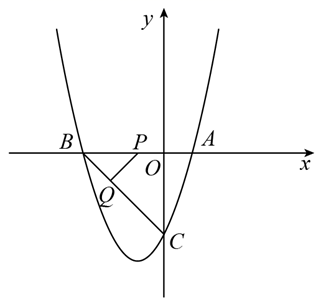 已知二次函数 $y = x^{2} + 2 b x - 3 b$ .

(1)、当该二次函数的图象经过点 $A (1 ， 0)$ 时，求该二次函数的表达式；

(2)、在(1) 的条件下，二次函数图象与x轴的另一个交点为点B，与y轴的交点为点C，点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动，直到其中一点到达终点时，两点停止运动，求△BPQ面积的最大值；

(3)、若对满足 $x \geq 1$ 的任意实数x，都使得 $y \geq 0$ 成立，求实数b的取值范围.

查看试题解析
25. 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆，如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨，每辆B型货车最多可装甲种货物5吨和乙种货物7吨.

(1)、装货时按此要求安排A、B两种货车的辆数，共有几种方案？

(2)、使用A型车每辆费用为600元，使用B型车每辆费用800元.在上述方案中，哪个方案运费最省？最省的运费是多少元？

(3)、在（2）的方案下，现决定对货车司机发共2100元的安全奖，已知每辆A型车奖金为m元.每辆B型车奖金为n元，38＜m＜n.且m、n均为整数，求此次奖金发放的具体方案.

查看试题解析
26. 有长为 $l$ 的篱笆，利用它和房屋的一面长为60米的墙围成形状如图的院子，院子的一边为 $x$ .

(1)、利用含 $l$ ， $x$ 的代数式表示院子的面积 .

(2)、若 $l = 100$ 固定不变.
①若 $x$ 的取值分别是20，25，30时，请通过计算说明哪一种取法围成的院子面积最大？

②问： $x$ 的值可以取10吗？ ▲；可以取50吗？ ▲ .（直接回答是或否即可）

③通过②的解答，你能说出 $x$ 可以取值的范围 ▲ .（直接写出答案）

查看试题解析

27. 为了防控新冠疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到如下图表：

该地区每周接种疫苗人数统计表

周次

第1周

第2周

第3周

第4周

第5周

第6周

第7周

第8周

接种人数（万人）

该地区全民接种疫苗情况扇形统计图

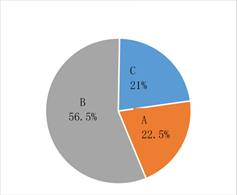
A：建议接种疫苗已接种人群

B：建议接种疫苗尚未接种人群

C：暂不建议接种疫苗人群

根据统计表中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点 $(3 ， 12)$ 、 $(8 ， 42)$ 作一条直线（如图所示，该直线的函数表达式为 $y = 6 x - 6$ ），那么这条直线可近似反映该地区接种人数的变化趋势.

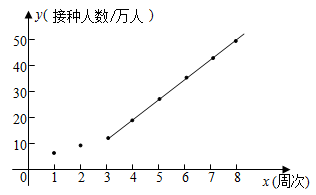
请根据以上信息，解答下列问题：

(1)、这八周中每周接种人数的平均数为万人：该地区的总人口约为万人；

(2)、若从第9周开始，每周的接种人数仍符合上述变化趋势.

①估计第9周的接种人数约为 ▲ 万人；

②专家表示：疫苗接种率至少达60%，才能实现全民免疫.那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？

(3)、实际上，受疫苗供应等客观因素，从第9周开始接种人数将会逐周减少

a (a > 0)

万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人.如果

a = 1.8

，那么该地区的建议接种人群最早将于第几周全部完成接种？

查看试题解析

28. 在平面直角坐标系中，点A、B的坐标分别为 $(a ， 0)$ ， $(0 ， b)$ ，其中a，b满足 $\sqrt{a - 2 b - 18} + | 2 a - 5 b - 30 | = 0$ .将点B向右平移26个单位长度得到点C，如图①所示.

(1)、求点A，B，C的坐标；

(2)、点M，N分别为线段 $B C$ ， $O A$ 上的两个动点，点M从点C向左以1.5个单位长度/秒运动，同时点N从点O向点A以2个单位长度/秒运动，如图②所示，设运动时间为t秒（ $0 < t < 15$ ）.
①当 $C M < A N$ 时，求t的取值范围；

②是否存在一段时间，使得 $S_{四边形 M N O B} > 2 S_{四边形 M N A C}$ ？若存在，求出t的取值范围；若不存在，说明理由.

查看试题解析

29. 班级书法小组购买“文房四宝”的数据如下，有部分数据因污损无法识别.

商品名	单价（元）	数量（件）	金额（元）
笔	20
墨		15	210
纸	24
砚	60	2
合计		43	922

(1)、此次购买的笔和纸各多少件？

(2)、若再次购买墨和砚共10件，且总价不超过370元，最多购买砚多少件？

(3)、若用420元购买墨和纸，在420元恰好用完的条件下，有哪些购买方案？

查看试题解析