浙教版备考2022年中考数学一轮复习专题6 一元一次方程及其应用
试卷更新日期:2022-01-06 类型:一轮复习
一、单选题
-
1. 某商店出售两件衣服,每件卖了200元,其中一件赚了25%,而另一件赔了20%.那这次交易中( )A、亏了10元钱 B、赚了10钱 C、赚了20元钱 D、亏了20元钱2. 若关于x的方程 是一元一次方程,则m值是( )A、1或2 B、1 或3 C、1 D、33. 若关于x的方程 有实数根,则实数k的取值范围是 ( )A、 B、 C、 D、4. 已知等式3a=2b+5,则下列等式变形错误的是( )A、3a﹣5=2b B、3a+1=2b+6 C、a= b+ D、3ac=2bc+55. 小迪想找一个解为x=-6的方程,那么她可以选择下面哪一个方程( )A、2x-1=x+7 B、 x= x-1 C、2(x+5)=-4-x D、 x=x-26. 如图,表中给出的是某月的月历,任意选取“H"型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是( )
 A、63 B、70 C、96 D、1057. 小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将-1、12、-3、14、15、-2、-4、13分别填入图中的圆圆内,使横、竖以及内外两围上的 4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )
A、63 B、70 C、96 D、1057. 小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将-1、12、-3、14、15、-2、-4、13分别填入图中的圆圆内,使横、竖以及内外两围上的 4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( ) A、12 或-3 B、-15或 13 C、12 或-16 D、-15或118. 幻方,又称纵横图.如图1是由数字1~9九个整数按照一定的规律排列成三行三列的一个方阵,每一横行、每一竖列以及两条斜线上的点数的和都相等.如图2所示的幻方中给出了三个数,则P处应该填的数字是( )
A、12 或-3 B、-15或 13 C、12 或-16 D、-15或118. 幻方,又称纵横图.如图1是由数字1~9九个整数按照一定的规律排列成三行三列的一个方阵,每一横行、每一竖列以及两条斜线上的点数的和都相等.如图2所示的幻方中给出了三个数,则P处应该填的数字是( )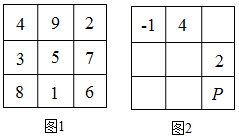 A、-1 B、0 C、1 D、29. 做完了一天的功课,立新老师组织学生乘坐小船泛游包河公园,若租用10座的小船m艘,则余下8人无座位:若租用16座的小船则可少租用1艘,且最后一艘小船还没坐满,则乘坐最后一艘16座小船的人数是( )A、32-6m B、40-6m C、64-8m D、16-2m10. 如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC=5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为t s,当以P,C,M为顶点的三角形与△QCN全等时,t的值为( )
A、-1 B、0 C、1 D、29. 做完了一天的功课,立新老师组织学生乘坐小船泛游包河公园,若租用10座的小船m艘,则余下8人无座位:若租用16座的小船则可少租用1艘,且最后一艘小船还没坐满,则乘坐最后一艘16座小船的人数是( )A、32-6m B、40-6m C、64-8m D、16-2m10. 如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC=5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为t s,当以P,C,M为顶点的三角形与△QCN全等时,t的值为( ) A、1或3 B、1或 C、1或 或 D、1或 或5
A、1或3 B、1或 C、1或 或 D、1或 或5二、填空题
-
11. 已知x=5是方程 的解,则 = .12. 如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度点运动至点A停止运动,设运动时间为t(单位:秒).
 (1)、当t=2时,点P表示的有理数为 .(2)、当点P与点B重合时t的值为 .(3)、①在点P由A到点B的运动过程中,点P与点A的距离为 . (用含t的代数式表示)
(1)、当t=2时,点P表示的有理数为 .(2)、当点P与点B重合时t的值为 .(3)、①在点P由A到点B的运动过程中,点P与点A的距离为 . (用含t的代数式表示)②在点P由点A到点B的运动过程中,点P表示的有理数为 . (用含t的代数式表示)
(4)、当点P表示的有理数与原点距离是2的单位长度时,t的值为 .13. 某服装店推出如下优惠方案:⑴一次性购物不超过100元不享受优惠;
⑵一次性购物超过100元但不超过300元一律9折;
⑶一次性购物超过300元一律8折.
小李两次购物分别付款85元,252元,如果他一次性购买以上两次相同的商品,他应付款元.
14. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为. 15. 如图,在△ABC中,∠ACB=90,AC=6,BC=8.点P从点A出发,沿折线AC—CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动,P、Q两点同时出发.分别过P、Q两点作PE⊥l于E,QF⊥l于F,当△PEC与△QFC全等时,CQ的长为.
15. 如图,在△ABC中,∠ACB=90,AC=6,BC=8.点P从点A出发,沿折线AC—CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动,P、Q两点同时出发.分别过P、Q两点作PE⊥l于E,QF⊥l于F,当△PEC与△QFC全等时,CQ的长为.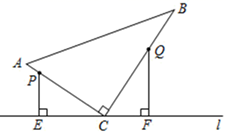 16. 如图, ,点 是线段 的中点,点 从点 出发,以 的速度向右移动,同时点 从点 出发,以 的速度向右移动到点 后立即原速返回点 ,当点 到达点 时, 两点同时停止运动.当 时,运动时间 的值是.
16. 如图, ,点 是线段 的中点,点 从点 出发,以 的速度向右移动,同时点 从点 出发,以 的速度向右移动到点 后立即原速返回点 ,当点 到达点 时, 两点同时停止运动.当 时,运动时间 的值是.
三、综合题
-
17. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.结合数轴与绝对值的知识回答下列问题:
 (1)、探究:
(1)、探究:①数轴上表示1和6的两点之间的距离是;
②数轴上表示﹣2和7的两点之间的距离是;
③数轴上表示﹣9和﹣3的两点之间的距离是 .
(2)、归纳:数a和数b的两点之间的距离可以表示为 .
(3)、应用:如果数a和3的两点之间的距离是15,则可记为:|a﹣3|=15,那么a的值为多少.
18. 阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|;当A、B两点都不在原点时,
①如图2,点A、B都在原点的右边|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图4,点A、B在原点的两边,|AB|=|OB|+|OA|=|a|+|b|=a+(﹣b)=|a﹣b|

回答下列问题:
(1)、数轴上表示2和5的两点之间的距离是 , 数轴上表示﹣2和﹣5的两点之间的距离是 , 数轴上表示1和﹣3的两点之间的距离是;(2)、数轴上表示x和﹣1的两点A和B之间的距离是 , 如果|AB|=2,那么x为;(3)、代数式|x+1|+|x﹣2|取最小值时,相应的整数x的取值是 .19. 综合与探究数轴是一个非常重要的数学工具,它使数和数轴上的点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小明在一条长方形纸带上画了一条数轴,进行如下操作探究:
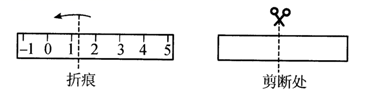 (1)、操作1:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示数 的点与表示数的点重合.(2)、操作2:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示 的点与表示数的点重合.(3)、操作3:如图,在数轴上剪下6个单位长度(从 到5)的一条线段,并把这条线段沿某点向左折叠,然后在重叠部分的某处剪一刀得到三条线段,发现这三条线段的长度之比为1:1:2,则折痕处对应的点表示的数可能是几?20. 为了严格控制水果质量,某果园建立了严格的果品标准,按照“糖酸度、鲜度、细嫩度、香味、安全性”将果园内种植的红富士苹果分成了18个等级,1级红富士的品质最好,2级次之,以此类推,第18级品质最差,果园在销售红富士时,制定销售价格如下:第9级的红富士售价为16元/千克,从第9级起,品质每提升1级,每千克的售价将提升0.5元;品质每下降1级,每千克的售价将降低0.4元.(1)、若红富士的等级为n , 用含n的代数式表示该级的售价(单位:元/千克);
(1)、操作1:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示数 的点与表示数的点重合.(2)、操作2:折叠纸带,使数轴上表示 的点与表示 的点重合,则表示 的点与表示数的点重合.(3)、操作3:如图,在数轴上剪下6个单位长度(从 到5)的一条线段,并把这条线段沿某点向左折叠,然后在重叠部分的某处剪一刀得到三条线段,发现这三条线段的长度之比为1:1:2,则折痕处对应的点表示的数可能是几?20. 为了严格控制水果质量,某果园建立了严格的果品标准,按照“糖酸度、鲜度、细嫩度、香味、安全性”将果园内种植的红富士苹果分成了18个等级,1级红富士的品质最好,2级次之,以此类推,第18级品质最差,果园在销售红富士时,制定销售价格如下:第9级的红富士售价为16元/千克,从第9级起,品质每提升1级,每千克的售价将提升0.5元;品质每下降1级,每千克的售价将降低0.4元.(1)、若红富士的等级为n , 用含n的代数式表示该级的售价(单位:元/千克);①当n<9时,售价为 元/千克;
②当n>9时,售价为 元/千克;
(2)、水果店老板小蓓计划在该果园购进5级红富士300千克,果园负责送货上门,但要收200元的运费,因小蓓是果园的老客户,果园负责人给出了如下两种优惠方案:方案一:降价5%,并减免全部运费;方案二:降价8%,但运费不减.
请你帮小蓓计算哪种优惠方案更加合算.
21. 生活与数学:如图①,将正偶数按每行8个数排列: (1)、吉姆同学按图②的方式在图①中圈出2×2个数,正方形的方框内的四个数的和是44,那么第一个数是.
(1)、吉姆同学按图②的方式在图①中圈出2×2个数,正方形的方框内的四个数的和是44,那么第一个数是. (2)、玛丽按图③的方式也在图①中圈出2×2个数,斜框内的四个数的和可能( )A、50 B、44 C、48 D、96(3)、莉莉按图④的方式在图①圈出5个数,呈十字框形,它们的和是200,则中间的数是.(4)、托马斯按图⑤的方式在图①画了一个斜框,斜框内9个数的和能为270吗?若能,请写出斜框的中间一个数是多少?若不能,请说明理由.
(2)、玛丽按图③的方式也在图①中圈出2×2个数,斜框内的四个数的和可能( )A、50 B、44 C、48 D、96(3)、莉莉按图④的方式在图①圈出5个数,呈十字框形,它们的和是200,则中间的数是.(4)、托马斯按图⑤的方式在图①画了一个斜框,斜框内9个数的和能为270吗?若能,请写出斜框的中间一个数是多少?若不能,请说明理由. 22. 定义:对于一个两位数x,如果x满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“标准数”,将一个“标准数”的个位数字与十位数字对调后得到一个新的两位数,将这个新两位数与原两位数求和,再除以11所得的商记为S(x).例如,当x=13,对调个位数字与十位数字得到的新两位数31,新两位数与原两位数的和为13+31=44,和44除以11的商为44÷11=4,所以S(13)=4.(1)、计算:S(92)=;(2)、若一个“标准数”y的十位数字是k,个位数字是2(k﹣2),且S(y)=14,求y;(3)、经思考,小聪同学发现:“若S(x)=5,则“标准数”x的个位数字与十位数字之和一定为5”,请判断小聪同学的发现是否正确?如果正确,说明理由;如果不正确,举出反例.23. 目前,新型冠状病毒在我国虽可控可防,但不可松懈某校欲购置规格分别为 和 的甲、乙两种免洗手消毒液若干瓶,已知购买1瓶甲和1瓶乙免洗手消毒液需要32元,购5瓶甲和3瓶乙免洗手消毒液需要120元.
22. 定义:对于一个两位数x,如果x满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“标准数”,将一个“标准数”的个位数字与十位数字对调后得到一个新的两位数,将这个新两位数与原两位数求和,再除以11所得的商记为S(x).例如,当x=13,对调个位数字与十位数字得到的新两位数31,新两位数与原两位数的和为13+31=44,和44除以11的商为44÷11=4,所以S(13)=4.(1)、计算:S(92)=;(2)、若一个“标准数”y的十位数字是k,个位数字是2(k﹣2),且S(y)=14,求y;(3)、经思考,小聪同学发现:“若S(x)=5,则“标准数”x的个位数字与十位数字之和一定为5”,请判断小聪同学的发现是否正确?如果正确,说明理由;如果不正确,举出反例.23. 目前,新型冠状病毒在我国虽可控可防,但不可松懈某校欲购置规格分别为 和 的甲、乙两种免洗手消毒液若干瓶,已知购买1瓶甲和1瓶乙免洗手消毒液需要32元,购5瓶甲和3瓶乙免洗手消毒液需要120元. (1)、求甲、乙两种免洗手消毒液的单价.(2)、该校在校师生共1000人,平均每人每天都需使用 的免洗手消毒液,若校方采购甲、乙两免洗手消毒液共花费4000元,则这批消毒液可使用多少天?(3)、为节约成本,该校购买散装免洗手消毒液进行分装,现需将 的免洗手消毒液全部装入最大容量分别为 和 的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗 ,请问如何分装能使总损耗最小,求出此时需要的两种空瓶的数量.24. 2021年十一国庆期间,鳌江银泰商场打出促销广告,如下表所示:
(1)、求甲、乙两种免洗手消毒液的单价.(2)、该校在校师生共1000人,平均每人每天都需使用 的免洗手消毒液,若校方采购甲、乙两免洗手消毒液共花费4000元,则这批消毒液可使用多少天?(3)、为节约成本,该校购买散装免洗手消毒液进行分装,现需将 的免洗手消毒液全部装入最大容量分别为 和 的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗 ,请问如何分装能使总损耗最小,求出此时需要的两种空瓶的数量.24. 2021年十一国庆期间,鳌江银泰商场打出促销广告,如下表所示:优惠
条件
一次性购物
不超过200元
一次性购物超过200
元,但不超过600元
一次性购物
超过600元
优惠
办法
没有
优惠
全部按九折
优惠
其中600元扔按九折优惠,
超过600元部分按八折优惠
用代数式表示(所填结果需化简):
(1)、设一次性购买的物品原价为x元,当原价x超过200元,但不超过600元时,实际付款为元;当原价x超过600元时,实际付款为元.
(2)、若甲购物时一次性付款580元,则所需物品的原价是多少元?(3)、若乙分两次购物,两次所购物品的原价之和为1200元(第二次所购物品的原价高于第一次),两次实际付款共1068元,则乙两次购物时,所需物品的原价分别是多少元?25. 观察下面的等式:;
;
;
;
.
回答下列问题:
(1)、填空: ;(2)、已知 ,则 的值是;(3)、设满足上面特征的等式最左边的数为 ,求 的最大值,并写出此时的等式.26. 如图1,在一条可以折叠的数轴上,点A,B分别表示数﹣9和4.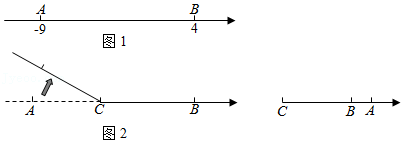 (1)、A,B两点之间的距离为.(2)、如图2,如果以点C为折点,将这条数轴向右对折,此时点A落在点B的右边1个单位长度处,则点C表示的数是(3)、如图1,若点A以每秒3个单位长度的速度沿数轴向右运动,点B以每秒2个单位长度的速度也沿数轴向右运动,那么经过多少时间,A.B两点相距4个单位长度?27. 家乐福超市出售甲、乙两种商品,甲种商品每件进价20元,售价35元;乙种商品每件进价30元,售价50元.(1)、若该超市同时购进甲、乙两种商品共100件,且使这100件商品的总利润(利润=售价﹣进价)为1800元,需购进甲、乙两种商品各多少件?(2)、在“元旦”期间,该超市对甲、乙两种商品进行如下优惠促销活动:
(1)、A,B两点之间的距离为.(2)、如图2,如果以点C为折点,将这条数轴向右对折,此时点A落在点B的右边1个单位长度处,则点C表示的数是(3)、如图1,若点A以每秒3个单位长度的速度沿数轴向右运动,点B以每秒2个单位长度的速度也沿数轴向右运动,那么经过多少时间,A.B两点相距4个单位长度?27. 家乐福超市出售甲、乙两种商品,甲种商品每件进价20元,售价35元;乙种商品每件进价30元,售价50元.(1)、若该超市同时购进甲、乙两种商品共100件,且使这100件商品的总利润(利润=售价﹣进价)为1800元,需购进甲、乙两种商品各多少件?(2)、在“元旦”期间,该超市对甲、乙两种商品进行如下优惠促销活动:打折前一次性购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过500元
售价一律打九折
超过500元
售价一律打八折
按上述优惠条件,若小张第一天只购买甲种商品一次性付款210元,第二天只购买乙种商品打折后一次性付款440元,那么这两天他在该超市购买甲、乙两种商品一共多少件?
28. 如图,已知AB∥CD , P是直线AB , CD间的一点,PF⊥CD于点F , PE交AB于点E , ∠FPE=120°. (1)、求∠AEP的度数;(2)、射线PN从PF出发,以每秒30°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动,若射线PN , 射线EM同时开始运动,设运动时间为t秒.
(1)、求∠AEP的度数;(2)、射线PN从PF出发,以每秒30°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动,若射线PN , 射线EM同时开始运动,设运动时间为t秒.①当∠MEP=15°时,求∠EPN的度数;
②当EM∥PN时,直接写出t的值.