2021-2022学年浙教版数学九上各地期末优生突击训练
试卷更新日期:2022-01-06 类型:复习试卷
一、综合题
-
1. 某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=﹣2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1=x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.(1)、试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售时间x(天)之间的函数关系式;(2)、请问在这30天的销售期中,哪一天的日销售利润最大?并求出这个最大利润值.
(注:销售利润=销售收入﹣购进成本)
2. 如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按逆时针旋转得到△ADC,连接OD,OA. (1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.3. 转转盘和摸球是等可能概率下的经典模型.(1)、在一个不透明的口袋中,放入除颜色外其余都相同的4个小球,其中1个白球,3个黑球搅匀后,随机同时摸出2个球,求摸出两个都是黑球的概率(要求采用树状图或列表法求解);(2)、如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).
(1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.3. 转转盘和摸球是等可能概率下的经典模型.(1)、在一个不透明的口袋中,放入除颜色外其余都相同的4个小球,其中1个白球,3个黑球搅匀后,随机同时摸出2个球,求摸出两个都是黑球的概率(要求采用树状图或列表法求解);(2)、如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).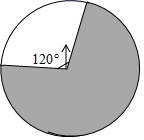 4. 只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17(1)、从7、11、13、17这4个素数中随机抽取一个,则抽到的数是7的概率是 .(2)、从7、11、13、17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.5. 如图,点O是等边三角形ABC内部一点,且满足∠BOC=150°,将△BOC绕点C按顺时针旋转至△ADC的位置,连接OD,OA.
4. 只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17(1)、从7、11、13、17这4个素数中随机抽取一个,则抽到的数是7的概率是 .(2)、从7、11、13、17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.5. 如图,点O是等边三角形ABC内部一点,且满足∠BOC=150°,将△BOC绕点C按顺时针旋转至△ADC的位置,连接OD,OA. (1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.6. 某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,分析得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1= x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.(1)、试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售间x(天)之间的函数关系式;(2)、请问在这30天的销售期中,哪一天的日销售利润最大?请求出这个最大利润值是多少?(注:销售利润=销售收入-购进成本)7. 如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.
(1)、求∠ODC的度数;(2)、若OB=2,OC=3,求AO的长.6. 某饰品店以20元/件的价格采购了一批今年新上市的饰品进行了为期30天的销售,销售结束后,分析得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:Q1= x+30(1≤x≤20),后10天的销售价格Q2则稳定在45元/件.(1)、试分别写出该商店前20天的日销售利润R1(元)和后10天的日销售利润R2(元)与销售间x(天)之间的函数关系式;(2)、请问在这30天的销售期中,哪一天的日销售利润最大?请求出这个最大利润值是多少?(注:销售利润=销售收入-购进成本)7. 如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.
 (1)、分别求抛物线和直线AC的解析式;(2)、在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1 , 且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.8. 北京将于2022年举办冬奥会和冬残奥会,中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者,他收集了如下图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好.
(1)、分别求抛物线和直线AC的解析式;(2)、在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)、在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1 , 且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.8. 北京将于2022年举办冬奥会和冬残奥会,中国将成为一个举办过五次各类奥林匹克运动会的国家小亮是个集邮爱好者,他收集了如下图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好. (1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票依次分别用字母A,B,C,D表示)9. 如图,在 中, ,D为AC延长线上一点, , ,过点D作DE//AB交BC的延长线于点E.
(1)、小亮从中随机抽取一张邮票是“冬残奥会吉祥物雪容融”的概率是;(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,请你用列表或画树状图的方法求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票依次分别用字母A,B,C,D表示)9. 如图,在 中, ,D为AC延长线上一点, , ,过点D作DE//AB交BC的延长线于点E.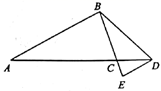 (1)、求证: ;(2)、求DE的长度.10. 如图, 在坐标平面内,三个顶点的坐标分别为 , , (正方形网格中,每个小正方形的边长均是1个单位长度).
(1)、求证: ;(2)、求DE的长度.10. 如图, 在坐标平面内,三个顶点的坐标分别为 , , (正方形网格中,每个小正方形的边长均是1个单位长度). (1)、 与 关于x轴成轴对称,请画出 ,并写出 点的坐标;(2)、以点 为位似中心,将 放大得到 ,放大前后的面积之比为 ,画出 ,使它与 在位似中心同侧,并写出 点的坐标;(3)、连接 、 ,判断 的形状并直接写出结论.11. 某商场试销一种成本为每件 元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于 ,经试销发现,销售量 (件)与销售单价 (元)符合一次函数(1)、若该服装获得利润为 (元),试写出利润 与销售单价 之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?(2)、若该商场获得利润不低于 元,试确定销售单价 的取值范围.12. 甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.(1)、求满足关于x的方程 有实数解的概率.(2)、求(1)中方程有两个相同实数解的概率.13. 如图,在平行四边形ABCD中,点E是边BC上的点,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、 与 关于x轴成轴对称,请画出 ,并写出 点的坐标;(2)、以点 为位似中心,将 放大得到 ,放大前后的面积之比为 ,画出 ,使它与 在位似中心同侧,并写出 点的坐标;(3)、连接 、 ,判断 的形状并直接写出结论.11. 某商场试销一种成本为每件 元的服装,规定试销期间销售单价不低于成本单价,且每件的利润率不得高于 ,经试销发现,销售量 (件)与销售单价 (元)符合一次函数(1)、若该服装获得利润为 (元),试写出利润 与销售单价 之间的关系式;销售单价定为多少时,商场可获得利润最大,最大利润是多少元?(2)、若该商场获得利润不低于 元,试确定销售单价 的取值范围.12. 甲、乙两同学投掷一枚骰子,用字母p、q分别表示两人各投掷一次的点数.(1)、求满足关于x的方程 有实数解的概率.(2)、求(1)中方程有两个相同实数解的概率.13. 如图,在平行四边形ABCD中,点E是边BC上的点,连接DE,F为线段DE上一点,且∠AFE=∠B. (1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 ,AF=4 ,求DE的长.14. 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C.
(1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6 ,AF=4 ,求DE的长.14. 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C. (1)、求反比例函数和一次函数的关系式;(2)、求△AOC的面积;(3)、求不等式kx+b< 的解集(直接写出答案).15. 二次函数y=x2﹣4mx+5(m为常数).(1)、当m=1时,
(1)、求反比例函数和一次函数的关系式;(2)、求△AOC的面积;(3)、求不等式kx+b< 的解集(直接写出答案).15. 二次函数y=x2﹣4mx+5(m为常数).(1)、当m=1时,①直接写出这个二次函数图象的对称轴和顶点坐标.
②若点(b,5)在这个抛物线上,求出b的值.
③当0≤x≤3时,求这个二次函数的最大值和最小值.
(2)、过点C(0,2)作直线l⊥y轴.①当直线l与抛物线有一个公共点时,求m的值.
②当x≥m时,抛物线y=x2﹣4mx+5(m为常数)的最低点到直线l的距离为1,请直接写出m的值.
16. 如图,在平面直角坐标系中,抛物线y= (x-1)2-2与x轴交于点A和点B(点A在点B的左侧),第一象限内的点C在该抛物线上. (1)、直接写出A、B两点的坐标;(2)、若 的面积为12,求点C坐标;(3)、在(2)问的条件下,直线y=mx+n经过点A、C, (x-1)2-2>mx+n时,直接写出x的取值范围.17. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如表:
(1)、直接写出A、B两点的坐标;(2)、若 的面积为12,求点C坐标;(3)、在(2)问的条件下,直线y=mx+n经过点A、C, (x-1)2-2>mx+n时,直接写出x的取值范围.17. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如表:x(元)
15
20
30
……
y(袋)
25
20
10
……
(1)、若日销售量y(袋)是每袋的销售价x(元)的一次函数,求y与x之间的函数关系式;(2)、假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元);①求w与x之间的函数关系式;
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
18. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点.线段AB的端点均在格点上.只用无刻度的直尺按下列要求在给定的网格中画图,不要求写画法,保留作图痕迹. (1)、在图①中画出线段AB的中点C;(2)、在图②中画出线段AB上的一点D,使AD:BD=4:5.19. 某班月考后,为了奖励成绩进步的学生,班主任老师准备了三种奖品:A笔记本、B中性笔、C棒棒糖,小文和小明从中随机选取一种奖品,且他们选取每种奖品的可能性相同.(1)、小文选棒棒糖的概率是 .(2)、请用列表或画树状图的方法求出小文和小明选择不同奖品的概率.(可用字母A、B、C代替奖品)20. 如图,在 中, , , , 于点 ,点 从点 出发,沿线段 向点 运动,点 从点 出发,沿线段 向点 运动,两点同时出发,速度都为每秒 个单位长度,当点 运动到点 时,两点都停止运动,设运动时间为 秒.
(1)、在图①中画出线段AB的中点C;(2)、在图②中画出线段AB上的一点D,使AD:BD=4:5.19. 某班月考后,为了奖励成绩进步的学生,班主任老师准备了三种奖品:A笔记本、B中性笔、C棒棒糖,小文和小明从中随机选取一种奖品,且他们选取每种奖品的可能性相同.(1)、小文选棒棒糖的概率是 .(2)、请用列表或画树状图的方法求出小文和小明选择不同奖品的概率.(可用字母A、B、C代替奖品)20. 如图,在 中, , , , 于点 ,点 从点 出发,沿线段 向点 运动,点 从点 出发,沿线段 向点 运动,两点同时出发,速度都为每秒 个单位长度,当点 运动到点 时,两点都停止运动,设运动时间为 秒. (1)、求线段 的长;(2)、设 的面积为 ,求 与 之间的函数关系式,并写出自变量的取值范围;(3)、当 为何值时, 与 相似?请直接写出 的值.21. 某批发商从某节能灯厂购进了50盒额定功率为 的节能灯.由于包装工人的疏忽,在包装时混进了 的节能灯.每盒中混入 的节能灯数如表:
(1)、求线段 的长;(2)、设 的面积为 ,求 与 之间的函数关系式,并写出自变量的取值范围;(3)、当 为何值时, 与 相似?请直接写出 的值.21. 某批发商从某节能灯厂购进了50盒额定功率为 的节能灯.由于包装工人的疏忽,在包装时混进了 的节能灯.每盒中混入 的节能灯数如表:每盒中混入 的节能灯数
0
1
2
3
4
盒数
14
25
9
1
1
(1)、平均每盒混入几个 的节能灯?(2)、从这50盒中任意抽取一盒,记事件 为:该盒中没有混入 的节能灯,求事件 的概率.22. 如图,菱形 的对角线 , 交于点 ,其中 .把 绕点 顺时针旋转得到 (点 的对应点为 ),旋转角为 ( 为锐角).连接 ,若 . (1)、求证: ;(2)、当 时,判断点 与直线 的位置关系,并说明理由.23. 在 中,∠B=90°,D是 外接圆上的一点,且点D是∠B所对的弧的中点.(1)、尺规作图:在图中作出点 ;(要求不写作法,保留作图痕迹)
(1)、求证: ;(2)、当 时,判断点 与直线 的位置关系,并说明理由.23. 在 中,∠B=90°,D是 外接圆上的一点,且点D是∠B所对的弧的中点.(1)、尺规作图:在图中作出点 ;(要求不写作法,保留作图痕迹) (2)、如图,连接 , ,过点 的直线交边 于点 ,交该外接圆于点 ,交 的延长线于点 , , 的延长线交于点 , .
(2)、如图,连接 , ,过点 的直线交边 于点 ,交该外接圆于点 ,交 的延长线于点 , , 的延长线交于点 , .
①若 , , ,求 的长;
②若 ,求 的度数
24. 如图,点P是等边 内一点, , , .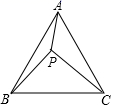 (1)、将 绕点B逆时针旋转60°得到 ,画出旋转后的图形;(2)、连接 ,判断 的形状并证明.25. 如图,已知在 中,D是边 上的一点, 的平分线交 于点E,且 .
(1)、将 绕点B逆时针旋转60°得到 ,画出旋转后的图形;(2)、连接 ,判断 的形状并证明.25. 如图,已知在 中,D是边 上的一点, 的平分线交 于点E,且 . (1)、求证: ;(2)、若 , ,求 的长.26. 如图所示, 与 相切于点C,线段 交 于点B.过点B作 交 于点D,连结 ,且 交 于点E.若 .
(1)、求证: ;(2)、若 , ,求 的长.26. 如图所示, 与 相切于点C,线段 交 于点B.过点B作 交 于点D,连结 ,且 交 于点E.若 . (1)、求 的大小和 的半径长.(2)、求由弦 与弧 所围成的阴影部分的面积(结果保留 ).
(1)、求 的大小和 的半径长.(2)、求由弦 与弧 所围成的阴影部分的面积(结果保留 ).