2021-2022学年浙教版数学七上各地期末优生突击训练

试卷更新日期：2022-01-06 类型：复习试卷

进入出卷网下载

一、综合题

1. 已知，在数轴上a、b、c所对应的点分别为A、B、C点：c是最小的两位正整数，且a，b满足（a＋26）²＋|b＋c|＝0，请回答问题：

(1)、求a，b，c的值.

(2)、若P为该数轴的一点，PA＝3PB，求点P表示的数．

(3)、若点M从A出发，以每秒1个单位长度的速度向终点C移动，同时点N从B出发，以每秒3个单位长度向A点运动，N点到达A点后，再立即以同样的速度运动到终点C，当某一个点到达点C时另一个点停止运动。设点M运动时间为t秒，当t为何值时，M，N两点间的距离为4．

查看试题解析
2. 某旅行社组织一批游客外出旅游，原计划租用45座客车若干辆，但有30人没有座位；若租用同样数量的60座客车，则多出两辆车，且其余客车恰好坐满.已知45座客车租金为每辆450元，60座客车租金为每辆650元，问：

(1)、这批游客的人数是多少?原计划租用多少辆45座客车?

(2)、请你设计一种租车方案，要求每位游客都有座位，费用又合算?

查看试题解析
3. 如图所示，点D、B、E是线段AC上的三点，D是线段AB的中点，

(1)、若点 E是BC的中点，BE= $\frac{1}{5}$ AC=2cm，求线段DE的长.

(2)、若AC=2DE=20，AD：EC=3：2，求线段EC的长.

查看试题解析
4. 某粮库3天内的粮食进出库的吨数为：+26，-32，-15，+34，-38，-20．问：

(1)、经过这3天，库里的粮食是增多了多少？还是减少了多少？

(2)、经过这3天，仓库管理员发现库里还存有520吨粮食，那么3天前库里存粮多少吨？

(3)、如果进出的装卸费都是每吨5元，那么这3天需要多少装卸费？

查看试题解析

5. 某超市开业，为了吸引顾客，实行优惠，方案如下表

购物数量	小于200元	满200，不超过500元	超过500元
优惠方式	不予优惠	标价9折优惠	500元（包括500元）给予9折优惠，超过500元部分给予8折优惠

(1)、小张付款170元，求购买了标价为多少元的商品？

(2)、小张购物x元（x＞500），求小张付款多少元？（用含x的代数式表示）

(3)、小张两次购买，第一次购买了标价为260元的商品，第二次购买了标价540元的商品，如果他把两次购买的商品合并为一次，请你计算，他可以节省多少元钱？

查看试题解析

6.

(1)、在下面带有箭头的直线上先确定好原点以及单位长度，然后在所得的数轴上把下列各数表示出来：﹣2，3.5， $- 1 \fra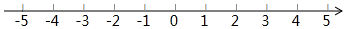c{1}{2}$ ，2.75， $2 \frac{1}{3}$ ，﹣3．

(2)、将上面6个数用“＜”连接．

查看试题解析

7. 某工艺厂计划一周生产工艺品2800个，计划每天生产400个，但实际每天生产量与计划相比有出入，如表是该工艺厂某周的生产情况（超产记为正、减产记为负）：

星期	一	二	三	四	五	六	日
增减（单位：个）	+6	﹣2	﹣4	+13	﹣10	+18	﹣9

(1)、该厂星期一生产工艺品的数量为个；

(2)、本周产量中最多的一天比最少的一天多生产个工艺品；

(3)、求该工艺厂本周实际生产工艺品多少个？

查看试题解析

8. 2020 年的“新冠肺炎”疫情的蔓延，市场上医用口罩销量大幅增加，某口罩加工厂为满足市场需求，计划每天生产6000个，由于各种原因与实际每天生产量相比有出入，下表是三月份某一周的生产情况（超产为正，减产为负，单位：个）．

星期	一	二	三	四	五	六	日
增减	$+ 150$	$- 200$	$+ 300$	$- 100$	$- 50$	$+ 250$	$+ 150$

(1)、产量最多的一天比产量最少的一天多生产多少个；

(2)、与原计划产量比较，这一周产量超产或减产多少个?

(3)、若口罩加工厂实行计件工资制，每生产一个口罩0.2元，则本周口罩加工厂应支付工人的工资总额是多少元?

查看试题解析

9. 2020年的“新冠肺炎”疫情的蔓延，使得医用口罩销量大幅增加，某口罩加工厂为满足市场需求计划每天生产5000个，由于各种原因实际每天生产量相比有出入，表格是二月份某一周的生产情况（超产为正，减产为负，单位：个）．

星期	一	二	三	四	五	六	日
增减	+100	-200	+400	-100	-100	+350	+150

(1)、根据记录可知前三天共生产多少个口罩；

(2)、产量最多的一天比产量最少的一天多生产多少个；

(3)、该口罩加工厂实行计件工资制，每生产一个口罩0.2元，本周口罩加工厂应支付工人的工资总额是多少元？

查看试题解析

10. 科技改变生活，当前网络销售日益盛行，许多农商采用网上销售的方式进行营销，实现脱贫致富．小王把自家种的柚子放到网上销售，计划每天销售100千克，但实际每天的销售量与计划销售量相比有增减，超过计划量记为正，不足计划量记为负．下表是小王第一周柚子的销售情况：

星期	一	二	三	四	五	六	日
柚子销售超过或不足计划量情况（单位：千克）	$+ 3$	$- 5$	$- 2$	$+ 11$	$- 7$	$+ 13$	$+ 5$

(1)、小王第一周销售柚子最多的一天比最少的一天多销售多少千克？

(2)、小王第一周实际销售柚子的总量是多少千克？

(3)、若小王按8元

/

千克进行柚子销售，平均运费为3元

/

千克，则小王第一周销售柚子一共收入多少元？

查看试题解析

11. 阅读下列材料，计算 $50 \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12})$ ．

(1)、解法1思路：原式 $= 50 \div \frac{1}{3} - 50 \div \frac{1}{4} + 50 \div \frac{1}{12} = 50 \times 3 - 50 \times 4 + 50 \times 12$ ；这种做法正确吗？答：．
解法2提示：先计算原式的倒数： $(\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \times \frac{1}{50} = \frac{1}{3} \times \frac{1}{50} - \frac{1}{4} \times \frac{1}{50} + \frac{1}{12} \times \frac{1}{50} = \frac{1}{300}$ ，故原式等于 $300$ ．

(2)、计算： $\frac{7}{8} \div (1 \frac{3}{4} - \frac{7}{3})$ = ．

(3)、请你用解法2的方法计算： $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$ ．

查看试题解析

12. 微信、快手、抖音等诸多平台的兴起，让越来越多的人做起了“微商”，很多农产品也改变了原来的销售模式，实行了网上销售，雷家店乡刚大学毕业的小亮把自家的核桃产品也放到了网上，实行包邮销售，他原计划每天卖

100

斤核桃，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负．单位：斤）：

星期	一	二	三	四	五	六	日
与计划量的差值	$+ 4$	$- 3$	$- 5$	$+ 14$	$- 8$	$+ 21$	$- 6$

(1)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售斤；

(2)、本周实际销售总量是否达到了计划数量？请说明理由．

(3)、若目前每斤核桃按

15

元出售，每斤核桃的运费平均

2

元，那么小亮本周一共收入多少元？

查看试题解析

13. 某公路检修队乘车从 $A$ 地出发，在南北走向的公路上检修道路，规定向南走为正，向北走为负，从出发到收工时所行驶的路程记录如下（单位：千米）：+2，-8，+5，-7，+10，-6，-7，+12．

(1)、收工时，检修队在 $A$ 地的哪边？距 $A$ 地多远？

(2)、在汽车行驶过程中，若每行驶1千米耗油0.2升，则检修队从 $A$ 地出发到回到 $A$ 地，汽车共耗油多少升？

(3)、请直接回答出在检修过程中，检修队最远离 $A$ 地多远？

查看试题解析

14. 在抗击新冠疫情的斗争中，某口罩厂全面提高生产能力，计划每天生产300包口罩，由于各种原因，实际每天的产量与计划有出入，下表为某周生产的增减情况（超产为正，不足为负）．

星期	一	二	三	四	五	六	日
增减	+5	﹣2	﹣4	+13	﹣10	+16	﹣9

(1)、产量最多的一天是包，最少的一天是包．

(2)、这一周共生产口罩多少包？

(3)、该工厂实行计件工资，每生产一包口罩可得50元，每超过计划一包另奖励15元，每少于计划生产一包扣30元，那么该厂工人本周前两天的工资分别是多少元？

查看试题解析

15. 老师写出一个整式（ax²+bx﹣3）﹣（2x²﹣3x）（其中a、b为常数），然后让同学给a、b赋予不同的数值进行计算．

(1)、甲同学给出了一组数据，最后计算的结果为﹣x²+4x﹣3，则甲同学给出a、b的值分别是a＝， b＝；

(2)、乙同学给出一组数，计算的最后结果与x的取值无关，求出b^a+ab的值．

查看试题解析
16. 如图所示是一个长方形．

(1)、根据图中尺寸大小，用含 $x$ 的代数式表示阴影部分的面积 $S$ ；

(2)、若 $x = 3$ ，求 $S$ 的值．

查看试题解析
17. 有理数a、b、c在数轴上的位置如图：

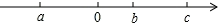(1)、判断正负，用“＞”或“＜”填空：b﹣c 0，b﹣a 0，c﹣a 0．

(2)、化简：|b﹣c|+|b﹣a|﹣|c﹣a|．

查看试题解析
18. 盐外第18届运动会，初一某班需要购买运动鞋和短裤，运动鞋每双定价200元，短裤每条定价50元．某商店开展促销活动，可以同时向客户提供两种优惠方案：
方案一：买一双运动鞋送一条短裤；

方案二：运动鞋和短裤都按定价的90%付款．

现某班要购买运动鞋20双，短裤x条（x超过20）．

(1)、若该班按方案一购买，需付款元；若该班按方案二购买，需付款元（用含x式子表示）；

(2)、当x=30时，哪种方案更划算？请通过计算说明理由；

(3)、若两种方案可以同时使用，当x=40时，你能给出一种最为省钱的购买方案吗？试写出你的购买方案，并计算该方案所需要付款金额．

查看试题解析
19. 一名足球守门员练习折返跑，从球门的位置出发，向前记作正数，返回记作负数，他的记录如下（单位：米）： $+ 5 ， - 3 ， + 10 ， - 8 ， - 6 ， + 12 ， - 10$ ．

(1)、守门员是否回到了原来的位置？

(2)、守门员离开球门的位置最远是多少？

(3)、守门员一共走了多少路程？

查看试题解析

20. 某电动车一周计划生产1400辆电动车，平均每天生产200辆，由于各种原因实际每天的产量与计划的产量相比有出入，下表是某周的生产情况（超产为正，减产为负，单位：辆）：

星期	一	二	三	四	五	六	日
增减	+5	-2	-4	+13	-10	+16	-9

根据记录可知，

(1)、前三天共生产了辆自行车；

(2)、产量最多的一天比产量最少的一天多多少辆？

(3)、该厂实行计件工资制，一周结算一次，每辆车60元，超额完成任务则超额部分每辆再奖15元，少生产一辆倒扣15元，那么该厂工人这一周的工资总额为多少元．

查看试题解析

21. 甲，乙两人相约一起到某书店购书，恰逢该书店举办全场9.5折的优惠活动，甲、乙两人在该书店共购书15本，优惠前甲平均每本书的价格为20元，乙平均每本书的价格为25元，优惠后甲，乙两人的书费共323元．

(1)、求甲、乙各购书多少本？

(2)、该书店凭会员卡当日可以在原价基础上享受全场8.5折优惠，办理一张会员卡需交20元工本费，如果甲、乙两人付费前立即合办一张会员卡，那么比两人不办会员卡购书共可节省多少钱？

查看试题解析
22. 如图，已知直线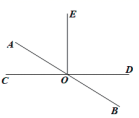 $A B$ ， $C D$ 相交于点 $O$ ， $∠ A O E$ 与 $∠ A O C$ 互余．

(1)、若 $∠ B O D = 32 °$ ，求 $∠ A O E$ 的度数；

(2)、若 $∠ A O D ： ∠ A 0 C = 5 ： 1$ ，求 $∠ B O E$ 的度数．

查看试题解析
23. 全球新冠疫情爆发后，口罩成了急需物资，中国企业积极采购机械生产口罩，为全球抗击疫情作出了贡献．某企业准备采购 $A$ 、 $B$ 两种机械共15台，用于生产医用口罩和N95医用防护口罩， $A$ 种机械每天每台可以生产医用口罩7万个， $B$ 种机械每天每台可以生产N95医用防护口罩2万个，根据疫情需要每天生产的医用口罩要求是N95医用防护口罩的4倍．

(1)、求该企业 $A$ 、 $B$ 两种机械各需要采购多少台？

(2)、设该企业每天生产数量相同的同一类型口罩，每天销售9万元，并提供优惠政策：购买不超过10天不优惠，超过10天不超过20天的部分打九折，超过20天不超过30天的部分打8折，超过30天的部分打7折．
①某国内医疗机构购买了该企业2周的口罩产量，问应付多少钱？

②某国外医疗机构一次性付款207万元，问医疗机构购买了多少天的口罩产量？

查看试题解析
24. 如图，已知 $O E$ 是 $∠ A O C$ 的角平分线， $O D$ 是 $∠ B O C$ 的角平分线．

(1)、若 $∠ A O E = 70 °$ ， $∠ C O D = 20 °$ ，求 $∠ A O B$ 的度数；

(2)、若 $∠ D O E = 45 °$ ，且 $∠ A O C + ∠ B O C = 180 °$ ，求 $∠ C O D$ 的度数．

查看试题解析
25. 为了加快社会主义新农村建设，党中央、国务院决定：凡农民购买家电或摩托车均享受政府13%的补贴．李伯伯家今年购买一台彩电和一辆摩托车，已知彩电的单价为 $a$ 元，摩托车的单价比所买彩电单价的2倍还多 $\frac{a}{3}$ 元．

(1)、在不享受政府补贴的情况下，李伯伯购买彩电和摩托车一共需要多少钱？

(2)、如果彩电的单价为1500元，那么李伯伯能领到多少钱的补贴款？

查看试题解析
26. 已知 $∠ A O B = 60 °$ ，求：

(1)、如图1， $O C$ 为 $∠ A O B$ 内部任意一条射线， $O M$ 平分 $∠ A O C$ ， $O N$ 平分 $∠ B O C$ ，求 $∠ M O N =$ ．

(2)、如图2，当 $O C$ 旋转到 $∠ A O B$ 的外部时， $∠ M O N$ 的度数会发生变化吗？请说明原因；

(3)、如图3，当 $O C$ 旋转到 $∠ A O B$ （ $∠ B O C < 120 °$ ）的外部且射线 $O C$ 在 $O B$ 的下方时， $O M$ 平分 $∠ A O C$ ，射线 $O N$ 在 $∠ B O C$ 内部， $∠ N O C = \frac{1}{4} ∠ B O C$ ，求 $∠ C O M - \frac{2}{3} ∠ B O N$ 的值？

查看试题解析