吉林省白山市临江2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-01-05 类型：期末考试

进入出卷网下载

一、选择题（每小题2分，共12分）

1. 以下四家银行的行标图中，是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列运算正确的是（）

A、（a+b）²=a²+b² B、（﹣2a²b）³=﹣8a⁵b³ C、a⁶÷a³=a² D、a³•a²=a⁵

查看试题解析
3. 石墨烯（Graphene）是人类已知强度最高的物质，据科学家们测算，要施加55牛顿的压力才能使0.000001米长的石墨烯断裂，其中0.000001用科学记数法表示为（）

A、1×10^﹣6 B、10×10^﹣7 C、0.1×10^﹣5 D、1×10⁶

查看试题解析
4. 如图，在△ABC中，∠B＝90°，∠A＝30°，作AC的垂直平分线交AB于点D，交AC于点E，若DE＝3，则BD的长度是（）

A、3 B、2 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
5. 下列约分正确的是（）

A、 $\frac{x + y}{x^{2} + x y}$ ＝ $\frac{1}{x}$ B、 $\frac{x^{6}}{x^{2}}$ ＝x³ C、 $\frac{x + y}{x + y} = 0$ D、 $\frac{2 x y^{2}}{4 x^{2} y}$ ＝ $\frac{1}{2}$

查看试题解析
6. 如图，AE、AD分别是△ABC的高和角平分线，∠B＝36°，∠C＝76°，则∠DAE的度数为（）

A、40° B、20° C、18° D、38°

查看试题解析

二、填空题（每小题3分，共24分）

7. 计算：（﹣3）⁰＝

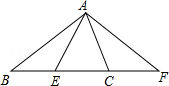
查看试题解析
8. 写出点M（﹣2，3）关于x轴对称的点的坐标

查看试题解析
9. 已知正n边形的一个内角为135°，则边数n的值是

查看试题解析
10. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为0，则x＝

查看试题解析
11. 已知（x+4）（x﹣9）＝x²+mx﹣36，则m的值为

查看试题解析
12. 如图，已知△ABC≌△AFE，若∠ACB＝65°，则∠EAC＝

查看试题解析
13. 两根木棒分别长3cm、7cm，第三根木棒与这两根木棒首尾依次相接构成三角形，如果第三根木棒的长为偶数（单位：cm），那么所构成的三角形周长为 cm

查看试题解析
14. 如图，已知∠AOB＝60°，点P在边OA上，OP＝10，点M、N在边OB上，PM＝PN，若MN＝2，则OM＝

查看试题解析

三、解答题（每小题5分，共20分）

15. 计算： $a^{- 2} b^{2}$ • $(a^{2} b^{- 2})^{- 3} \div (a^{- 4})^{2}$

查看试题解析
16. 分解因式：x³y﹣6x²y²+9xy³

查看试题解析
17. 先化简，再求值：（x+2）²+（2x+1）（2x﹣1）﹣4x（x+1），其中x＝﹣1

查看试题解析
18. 解方程： $\frac{x}{x + 2}$ + $\frac{1}{x - 2}$ =1

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，在平面直角坐标系中，已知A（1，4）、B（3，1）、C（3，5），△ABC关于y轴的对称图形为△A₁B₁C₁

(1)、请画出△ABC关于y轴对称图形△A₁B₁C_1，并写出三个顶点的坐标A₁（），
B₁（），C₁（）

(2)、在y轴上取点D，使得△ABD为等腰三角形，这样的点D共有个

查看试题解析
20. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．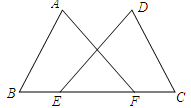

查看试题解析
21. 某学校需要购进甲、乙两种电脑，经调查，每台甲种电脑的价格比每台乙种电脑的价格少0.2万元，且用12万元购买的甲种电脑的数量与用20万元购买的乙种电脑的数量相同．求每台甲种电脑价格．

查看试题解析
22. 如图
如图1，在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，AC＝8，点P为AC边上的一个动点，过点P作PD⊥AB于点D，求PB+PD的最小值。请在横线上补充其推理过程或理由。
解：如图2，延长BC到点B′，使得BC＝B′C，连接PB′
∵ ∠ACB＝90°（已知）
∴ （垂直的定义）
∴ PB＝（线段垂直平分线的性质）
∴ PB+PD＝PB′+PD（等式性质）
∴ 过点B′作B′D⊥AB于点D，交AC于点P，此时PB+PD取最小值
连接AB′，在△ABC和△AB′C中，
∵AC＝AC，∠ACB＝∠ACB′＝90°， ∴△ABC≌△AB′C（理由：）
∴ S_ABB′＝S_△ABC+＝2S_△ABC（全等三角形面积相等）
∵ S_△ABB′＝ $\frac{1}{2}$ AB﹒B'D＝ $\frac{1}{2}$ ×10B′D＝5B′D
2S_△ABC＝2× $\frac{1}{2}$ BC﹒AC＝2× $\frac{1}{2}$ ×6×8＝48
∴ （同一三角形面积相等）∴ B′D＝ $\frac{48}{5}$
∴

查看试题解析

五、解答题（每题8分，共16分）

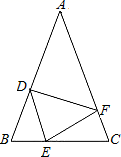
23. 如图，在△ABC中，AB＝AC ，点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．

(1)、求证：△DEF是等腰三角形；

(2)、当∠A＝40°时，求∠DEF的度数．

查看试题解析
24. 我们探究过三角形内角和等于180°，四边形内角和等于360°，请解决下面的问题：

(1)、如图1，∠A+∠B+∠C+∠D＝180°，则∠AOB+∠COD＝（直接写出结果）

(2)、连接AD、BC，若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线
①如图2，如果∠AOB＝110°，那么∠COD的度数为 ▲ （直接写出结果）
②如图3，若∠AOD＝∠BOC，AB与CD平行吗？请写出理由

查看试题解析

六、解答题（每题10分，共20分）

25. 防疫期间某工厂接到生产N95口罩和普通医用外科口罩共180万个的生产任务，该工厂不能同时生产两种口罩，且生产普通医用外科口罩的速度是生产N95口罩速度的2倍，生产40万个N95口罩比生产40万个普通医用外科口罩多用4天

(1)、求该工厂每天能生产N95口罩或生产普通医用外科口罩各多少万个？

(2)、若每生产一个N95口罩可获利0.6元，每生产一个普通医用外科口罩可获利0.25元，且生产工期不能超过26天，则工厂如何安排生产获利最多？最多获利多少万元？

查看试题解析
26. 【探索发现】等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A、B分别是y轴、x轴上两个动点，直角边 AC 交x轴于点D，斜边BC交y轴于点E

(1)、如图1，已知C点的横坐标为﹣1，请直接写出点A的坐标
图1

(2)、如图2，当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE
图2

(3)、【拓展应用】
如图3，若点A在x轴上，且A（﹣4，0），点B在y轴的正半轴上运动时，分别以OB、 AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC，连接CD交y轴于点P，当点B在y轴的正半轴上运动时，BP的长度是否变化？若变化请说明理由，若不变化，请直接写出BP的长度为

图3

查看试题解析