吉林省白山市临江2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-01-05 类型：期末考试

进入 出卷网 下载

一、选择题（每小题2分，共12分）

  • 1.  下列图形中，既是中心对称图形又是轴对称图形的是（      ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 抛物线y＝（x﹣1）2+2的顶点坐标是（       ）
    A、（1，2） B、（﹣1，2） C、（1，﹣2） D、（﹣1，﹣2）

    查看试题解析

  • 3.  下列方程式属于一元二次方程的是（       ）
    A、x3+x﹣3＝0 B、x2+1x＝2 C、x2+2xy＝1 D、x2＝2

    查看试题解析

  • 4.  如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠P＝36°，则∠ACB为（      ）

    A、54° B、72° C、108° D、144°

    查看试题解析

  • 5. 下列属于必然事件的是（      ）
    A、水滴石穿 B、水中捞月 C、大海捞针 D、守株待兔

    查看试题解析

  • 6. 如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（ ）

    A、3π B、3π2 C、6π D、24π

    查看试题解析

二、填空题（每小题3分，共24分）

  • 7. 已知x＝﹣1是关于x的方程ax2+bx﹣2＝0的一个根，则2021+2a﹣2b＝ 

    查看试题解析

  • 8. 中心角为30°的正多边形边数为 ．

    查看试题解析

  • 9. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了10条航线，则这个航空公司共有个飞机场

    查看试题解析

  • 10. 将二次函数y=-x2的图象向右平移两个单位长度，再向上平移三个单位长度，则所得图象的函数表达式为 

    查看试题解析

  • 11. 如图，⊙O的直径AB垂直于弦CD，垂足为E，如果∠B＝60°，AC＝6，则CD的长为

    查看试题解析

  • 12. 圆锥的底面圆的周长是4πcm，母线长是6cm，则该圆锥侧面展开图的圆心角的度数为

    查看试题解析

  • 13. 如图，二次函数y＝ax2+bx+c的图象开口向上，图象经过点（﹣1，2）和（1，0），且与y轴交于负半轴，给出六个结论：①a＞0；②b＞0；③c＞0；④a+b+c＝0；⑤b2﹣4ac＞0；⑥2a﹣b＞0，其中正确结论的序号是

    查看试题解析

  • 14. 已知关于x的二次函数y=x2-4x+m，在-1≤ x≤3 的取值范围内最大值为7，则该二次函数的最小值为

    查看试题解析

三、解答题（每小题5分，共20分）

  • 15.  用公式法解方程x2﹣3x+1＝0

    查看试题解析

  • 16.  已知二次函数y＝x2﹣mx+2m﹣4 

    证明：无论m取任何实数时，该函数图象与x轴总有交点

    查看试题解析

  • 17. 共享经济已经进入人们的生活，小明收集了共享出行、共享服务、共享物品、共享知识4个共享经济领域的图标，制成编号为A、B、C、D的四张卡片（除字母和内容外其余完全相同）现将这四张卡片背面朝上，洗匀放好

    (1)、小明从中随机抽取一张卡片是“共享服务”的概率是
    (2)、若随机抽取一张卡片不放回，再从余下的卡片中随机抽取一张，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率（卡片用编号表示）

    查看试题解析

  • 18.  如图，已知△ABC的三个顶点坐标分别为A（﹣2，4），B（﹣6，0），C（﹣1，1）

    将△ABC绕坐标原点O逆时针旋转90度，请在图中画出旋转后的图形△A1B1C1

    写出点A1的坐标为点C1关于坐标原点对称的点的坐标为 

    查看试题解析

四、解答题（每小题7分，共28分）

  • 19.  已知关于x的方程x2﹣2016x+m2﹣3m＝0的一个根与关于x的方程x2+2016x﹣m2+3m＝0的一个根互为相反数，求m的值

    查看试题解析

  • 20. 若一个函数的解析式等于另两个函数解析式的和，则这个函数称为另两个函数的“生成函数”。现有关于x的两个二次函数y1 ， y2 ， 且y1＝a（x﹣m）2+4（m＞0），y1与y2的“生成函数”为：y＝x2+4x+14；当x＝m时，y2＝15；二次函数y2的图象的顶点坐标为（2，k）
    (1)、求m的值
    (2)、求二次函数y1 ， y2的解析式

    查看试题解析

  • 21. 如图是一张长20cm、宽13cm的矩形纸板，将纸板四个角各剪去一个边长为xcm的正方形，然后将四周突出部分折起，可制成一个无盖纸盒

    (1)、这个无盖纸盒的长为cm，宽为cm （用含x的式子表示）
    (2)、若要制成一个底面积是144cm2的无盖长方体纸盒，求x的值

    查看试题解析

  • 22. 如图所示，正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接 四边形、内接五边形，点M、N分别从点B、C开始，以相同的速度在⊙O上逆时针运动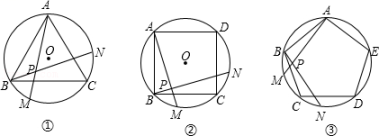

    (1)、求图①中∠APB的度数
    (2)、图②中∠APB的度数是 ， 图③中∠APB的度数是
    (3)、若推广到一般的正n边形情况，请写出∠APB的度数是 

    查看试题解析

五、解答题（每题8分，共16分）

  • 23.  某数学兴趣小组通过市场调查，得到某种运动服每月的销量与售价的相关信息如下表所示

    售价（元/件）

     100

     110

    120 

     130

    …

     月销量（件）

     200

    180 

     160

    140 

    …

    已知该运动服的进价为每件60元，设售价为x元

    (1)、请写出销售该运动服每件的利润是元（用含x的式子表示）
    (2)、请写出月销量y与售价x之间的函数关系式 
    (3)、设月利润为w元，请求出售价x为多少时，当月的利润最大，最大利润是多少？

    查看试题解析

  • 24. 如图，已知抛物线y＝1a（x﹣2）（x+a），其中a＞0，与x轴交于点B、C，与y轴交于点E
    (1)、若抛物线过点M（﹣2，﹣2），求实数a的值
    (2)、在（1）的条件下，解答下列问题：

    ① 求出△BCE的面积

    ② 在抛物线的对称轴上找一点H，使CH+EH的值最小，直接写出点H的坐标            ▲ 

    查看试题解析

六、解答题（每题10分，共20分）

  • 25.  如图，⊙O是△ABC的外接圆，BC为⊙O的直径，点E为△ABC的内心（三角形三个内角平分线的交点），连接AE并延长交⊙O于D点，连接BD并延长至F，使得BD＝DF，连接CF、BE

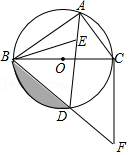    (1)、求证：DB＝DE
    (2)、求证：直线CF为⊙O的切线
    (3)、若CF＝4，求图中阴影部分的面积

    查看试题解析

  • 26. 如图，抛物线y＝ax2+bx+3（a，b是常数，且a≠0）与x轴交于A、B两点，与y轴交于点C，A、B两点的坐标分别是A（1，0）、B（﹣3，0），抛物线顶点为D

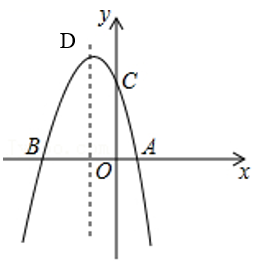    (1)、求出抛物线的解析式
    (2)、请直接写出顶点D的坐标为 ；直线BD的解析式为 
    (3)、若E为线段BD上的一个动点，其横坐标为m，过点E作EF⊥x轴于点F，求当m为何值时，四边形EFOC的面积最大？
    (4)、若点P在抛物线的对称轴上，且线段PA绕点P逆时针旋转90°后，点A的对应点A'恰好也落在此抛物线上，请直接写出点P的坐标 

    查看试题解析