湖北省武汉市江岸区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2022-01-05 类型:期末考试
一、单选题
-
1. -2021的倒数是( )A、-2021 B、 C、2021 D、2. 中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片,在指甲盖大小的尺寸上塞进了120亿个晶体管,是世界上最先进的具有人工智能的手机处理器,将120亿个用科学记数法表示为( )A、 个 B、 个 C、 个 D、 个3. 单项式-5ab3的系数是( )A、5 B、-5 C、4 D、34. 方程 的解是 ,则 ( )A、–8 B、0 C、2 D、85. 某正方体的平面展开图如图所示,则原正方体中与“斗”字所在的面相对的面上的字是( )
 A、青 B、来 C、春 D、用6. 下列四个生产生活现象,可以用公理“两点之间,线段最短”来解释的是( )A、用两个钉子可以把木条钉在墙上 B、植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上 C、打靶的时候,眼睛要与枪上的准星、靶心在同一直线上 D、为了缩短航程把弯曲的河道改直7. (古代数学问题)今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?设有x人,则根据题意列出方程正确的是( )A、8x+3=7x﹣4 B、8x﹣3=7x+4 C、8x﹣3=7x﹣4 D、8x+3=7x+48. 已知A=A0(1+mt)(m、A、A0均不为0),则t=( )A、. B、 C、 D、9. 如图,、、分别是 , , 的角平分线,则下列选项成立的( )
A、青 B、来 C、春 D、用6. 下列四个生产生活现象,可以用公理“两点之间,线段最短”来解释的是( )A、用两个钉子可以把木条钉在墙上 B、植树时,只要定出两棵树的位置,就能使同一行树坑在一条直线上 C、打靶的时候,眼睛要与枪上的准星、靶心在同一直线上 D、为了缩短航程把弯曲的河道改直7. (古代数学问题)今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?设有x人,则根据题意列出方程正确的是( )A、8x+3=7x﹣4 B、8x﹣3=7x+4 C、8x﹣3=7x﹣4 D、8x+3=7x+48. 已知A=A0(1+mt)(m、A、A0均不为0),则t=( )A、. B、 C、 D、9. 如图,、、分别是 , , 的角平分线,则下列选项成立的( ) A、 B、 C、 D、以上情况都有可能10. 在同一平面内,我们把两条直线相交将平面分得的区域数记为 , 三条直线两两相交最多将平面分得的区域数记为 , 四条直线两两相交最多将平面分得的区域数记为 条直线两两相交最多将平面分得的区域数记为 , 若 , 则 ( )A、 B、 C、 D、
A、 B、 C、 D、以上情况都有可能10. 在同一平面内,我们把两条直线相交将平面分得的区域数记为 , 三条直线两两相交最多将平面分得的区域数记为 , 四条直线两两相交最多将平面分得的区域数记为 条直线两两相交最多将平面分得的区域数记为 , 若 , 则 ( )A、 B、 C、 D、二、填空题
-
11. 的余角是.12. 单项式 的次数是 .13. 我们来定义一种运算: , 例如 , 按照这种定义,当成立时,则的值是.14. 现对某商品八折促销,为了使销售总金额不变,销售量要比按原价销售时增加的百分数是.15. 如图,动点 , , 分别从数轴 , , 的位置沿数轴正方向运动,速度分别为个单位长度/秒,个单位长度/秒,个单位长度/秒,线段的中点为 , 线段的中点为 , 线段的中点为 , 若为常数,则为.
 16. 有个自然数满足条件( , 并且)若 , 则.
16. 有个自然数满足条件( , 并且)若 , 则.三、解答题
-
17. 计算:(1)、(2)、18. 解方程:19. 先化简下式,再求值 , 其中20. 化简并填空(1)、当时,化简;(2)、当最小时,的最大值为.21. 角与线段的计算
 (1)、如图1,已知 , 为 中点, 为 中点,求(2)、如图2,已知 , , 若 , 求 .22. 滴滴打车是一种新的共享出行方式,滴滴打车有滴滴快车和优享专车两种出租车,他们的收费方式有所不同.
(1)、如图1,已知 , 为 中点, 为 中点,求(2)、如图2,已知 , , 若 , 求 .22. 滴滴打车是一种新的共享出行方式,滴滴打车有滴滴快车和优享专车两种出租车,他们的收费方式有所不同.优享专车:每千米收费2.5元,不收其他费用,
滴滴快车:
计费项目
起步价
里程费
远途费
计费价格
8
元/千米
元/千米
注:车费由起步价、里程费、远途费三部分组成,其中起步价包含里程2千米;里程千米的部分按计价标准收取里程费;远途费的收取方式为:行车15千米以内(含15千米)不收远途费,超过15千米的,超出部分每千米加收元.
(1)、若张老师选择乘坐优享专车3千米需付元;若张老师选择乘坐滴滴快车3千米需付元;
若张老师选择乘坐优享专车20千米需付元;
若张老师选择乘坐滴滴快车20千米需付元;
(2)、若我校张老师需要乘滴滴打车到离家(为正整数)千米的学校上班,请问她该如何选择出行方式?23. 数形结合思想是通过数和形之间的对应关系和相互转化来解决问题的数学思想方法.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事休.”(1)、(问题背景)往返于甲、乙两地的客车,中途停靠2个车站(来回票价一样),可以从任意站点头票出发且任意两站间的票价都不同,共有种不同的票价,需准备种车票.
聪明的小周是这样思考这个问题的,她用 , , , , 4个点表示车站,每两站之间的票价用相应两点间的线段表示,共连出多少条线段,就有多少种不同的票价. (2)、(迁移应用) , , , , , 六支足球队进行单循环比赛,当比赛到某一天时,统计出 , , , , 五支队已经分别比赛了 , , , , 场球,则还没有与 队比赛的球队是队.(3)、(拓展创新)某摄制组从 市到 市有一天的路程,计划上午比下午多走100千米到 市吃午饭,但由于堵车,中午才赶到一个小镇,只行驶了上午原计划的三分之一,过了小镇,汽车行驶了400千米,傍晚才停下来休息,司机说,再走从 市到这里的路程的二分之一就到达目的地了,求 , 两市相距多少千米?24. 已知如图1,
(2)、(迁移应用) , , , , , 六支足球队进行单循环比赛,当比赛到某一天时,统计出 , , , , 五支队已经分别比赛了 , , , , 场球,则还没有与 队比赛的球队是队.(3)、(拓展创新)某摄制组从 市到 市有一天的路程,计划上午比下午多走100千米到 市吃午饭,但由于堵车,中午才赶到一个小镇,只行驶了上午原计划的三分之一,过了小镇,汽车行驶了400千米,傍晚才停下来休息,司机说,再走从 市到这里的路程的二分之一就到达目的地了,求 , 两市相距多少千米?24. 已知如图1,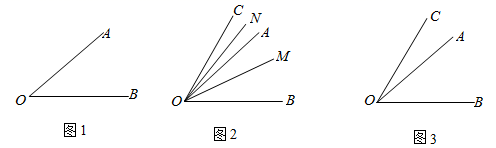 (1)、若 , 则 ;(2)、如图 , , 为 内部的一条射线, 是 四等分线,且 , 求 的值;(3)、如图3, , 射线 绕着 点从 开始以5度/秒的速度逆时针旋转一周至 结束,在旋转过程中,设运动的时间为 , 是 四等分线,且 , 当 在某个范围内 会为定值,请直接写出定值,并指出对应 的范围(本题中的角均为大于 且小于 的角).
(1)、若 , 则 ;(2)、如图 , , 为 内部的一条射线, 是 四等分线,且 , 求 的值;(3)、如图3, , 射线 绕着 点从 开始以5度/秒的速度逆时针旋转一周至 结束,在旋转过程中,设运动的时间为 , 是 四等分线,且 , 当 在某个范围内 会为定值,请直接写出定值,并指出对应 的范围(本题中的角均为大于 且小于 的角).