湖北省武汉市蔡甸区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2022-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. 2020年12月14日（周一）武汉市某学校操场上的气温为2℃，当时学校七年级1班教室内的气温是20℃，此时这个教室的室外的气温比室内气温低（）℃

A、18° B、 $- 18 °$ C、22° D、 $- 22 °$

查看试题解析
2. 若 $- 3 x^{2} y^{n}$ 与 $5 x^{m} y^{3}$ 是同类项，则m-n的值是（）

A、0 B、1 C、-1 D、5

查看试题解析
3. 香蕉的单价为 $a$ 元/千克，苹果的单价为 $b$ 元/千克，买2千克苹果和3千克香蕉共需（）元

A、 $a + b$ B、 $3 a + 2 b$ C、 $2 a + 3 b$ D、 $5 (a + b)$

查看试题解析
4. 用四舍五入法将201850精确到万位的近似值是（）.

A、 $2.0 \times 1 0^{5}$ B、 $2.1 \times 1 0^{5}$ C、 $2.2 \times 1 0^{5}$ D、 $2 \times 1 0^{5}$

查看试题解析
5. 在时刻9：30，墙上挂钟的时针与分针之间的夹角是（）

A、115° B、105° C、100° D、90°

查看试题解析
6. 如图所示的几何体是由五个小正方体搭建而成的，则从左面看得到的平面图形是（）

A、 B、 C、 D、

查看试题解析
7. 某学校有 $x$ 间男生宿舍和 $y$ 个男生，若每间宿舍住8个人，则还多4个人无法安置；若每间宿舍安排10个人，则还多6张空床位，据此信息列出方程，下列4个方程中正确的是（）.
① $8 x - 4 = 10 x + 6$ ② $\frac{y - 4}{8} = \frac{y + 6}{10}$ ③ $\frac{y + 4}{8} = \frac{y - 6}{10}$ ④ $8 x + 4 = 10 x - 6$

A、①③ B、②④ C、①② D、③④

查看试题解析
8. 解方程 $\frac{2 x + 1}{3} - \frac{10 x + 1}{6} = 1$ 时，去分母、去括号后，正确的结果是（）

A、 $4 x + 1 - 10 x + 1 = 1$ B、 $4 x + 2 - 10 x - 1 = 1$ C、 $4 x + 2 - 10 x - 1 = 6$ D、 $4 x + 2 - 10 x + 1 = 6$

查看试题解析
9. 如图， $D$ 、 $E$ 顺次为线段 $A B$ 上的两点， $A B = 19$ ， $B E - D E = 5$ ， $C$ 是 $A D$ 的中点，则 $A E - A C$ 的值是（）

A、5 B、6 C、7 D、8

查看试题解析
10. 将一副学生用三角板（一个锐角为30°的直角三角形，一个锐角为45°的直角三角形）如图叠放，则下列4个结论中正确的个数有（）
① $O E$ 平分 $∠ A O D$ ；② $∠ A O C = ∠ B O D$ ；③ $∠ A O C - ∠ C E A = 15 °$ ；④ $∠ C O B + ∠ A O D = 180 °$

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

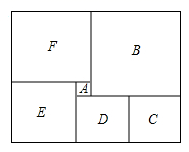
11. -5的相反数是， $- 5$ 的倒数是， $- 5$ 的绝对值是.

查看试题解析
12. 货轮 $O$ 在航行过程中，发现灯塔 $A$ 在它南偏西20°的方向上，同时在它北偏东78°方向上发现了客轮 $B$ ，则此时 $∠ A O B$ 的度数大小是.

查看试题解析
13. 计算 $- b - (2.6 b - 0.6 b)$ 的结果是.

查看试题解析
14. 一个角的一半比它的补角小30°，则这个角的度数是.

查看试题解析
15. 父亲和女儿的年龄之和是96，当父亲的年龄是女儿现在年龄的2倍时，女儿的年龄比父亲现在年龄的 $\frac{1}{3}$ 多2，则父亲现在的年龄是.

查看试题解析
16. 如图是由六个不同颜色的正方形组成的矩形，已知中间最小的一个正方形 $A$ 的边长为1，那么矩形中正方形 $E$ 的面积是.

查看试题解析

三、解答题

17. 计算：

(1)、 $3 \frac{1}{4} + (- 7) - (- 5 \frac{3}{4}) + 12$

(2)、 $- {(- 2)}^{2} + 2^{2} - {(- 1)}^{9} \times (\frac{1}{3} - \frac{1}{2}) + \frac{1}{6} - 8$

查看试题解析
18. 解方程：

(1)、 $3 (x - 3) = 2 (5 x - 7) + 6 (1 - x)$

(2)、 $\frac{x - 1}{0.3} - \frac{x + 2}{0.5} = 1.2$

查看试题解析
19. 先化简，再求值：
$3 a^{2} b - 2 a b^{2} - 2 (a b - \frac{3}{2} a^{2} b) + a b + 3 a b^{2}$ ，其中 $a = - 3$ ， $b = - 2$ .

查看试题解析
20. 某商场购进一批服装，一件服装的标价为400元.

(1)、若按标价的6折销售，则实际售价是多少？

(2)、在（1）的条件下销售这件服装仍可获利20%，问这件服装每件的进价为多少元？

查看试题解析

21. 某学校组织四名学生参加知识竞赛，知识竞赛共设20道选择题，各题分值相同，每题必答，下表记录了其中2名学生参赛后的得分情况.

参赛者	答对题数	答错题数	得分
$A$	18	2	86
$B$	17	3	79

(1)、参赛学生

C

得72分，他答对了几道题？答错了几道题？为什么？

(2)、参赛学生

D

说他可以得94分，你认为可能吗？为什么？

查看试题解析

22. 下表中有两种移动电话计费方式：

月使用费/元
主叫限定时间/ $m i n$
主叫超时费/元/ $m i n$
方式一
58
200
$x$
方式二
88
400
$x + 0.05$
其中，月使用费固定收，主叫不超过限定时间不再收费，主叫超过部分加收超时费.已知当方式一主叫超时20分钟，方式二主叫超时40分钟时，两种方式共收费160元.

(1)、求 $x$ 的值.

(2)、若每月主叫时间不超过400分钟，当主叫时间为多少分钟时，两种方式收费相同？

(3)、若每月主叫时间为700分钟，选择哪种方式计费更省钱？

查看试题解析
23. 点 $A$ 、 $B$ 在数轴上所对应的数分别是 $x$ 、 $y$ ，其中 $x$ 、 $y$ 满足 ${(x - 3)}^{2} + | y + 5 | = 0$ .

(1)、求 $x$ 、 $y$ 的值.

(2)、数轴上有一点 $M$ ，使得 $| A M | + | B M | = \frac{7}{4} | A B |$ ，求点 $M$ 所对应的数.

(3)、点 $D$ 是 $A B$ 的中点， $O$ 为原点，数轴上有一动点 $P$ ，直接写出 $| P A | + | P B |$ 的最小值是； $| P D | - | P O |$ 的最小值是； $| P A | + | P B | + | P D | - | P O |$ 取最小时，点 $P$ 对应的数 $a$ 的取值范围是.

查看试题解析
24. 已知 $O$ 为直线 $A B$ 上一点，射线 $O D$ 、 $O C$ 、 $O E$ 位于直线 $A B$ 上方， $O D$ 在 $O E$ 的左侧， $∠ A O C = 120 °$ ， $∠ D O E = α$ .

(1)、如图1， $α = 70 °$ ，当 $O D$ 平分 $∠ A O C$ 时，求 $∠ E O B$ 的度数.

(2)、如图2，若 $∠ D O C = 2 ∠ A O D$ ，且 $α < 80 °$ ，求 $∠ E O B$ （用 $α$ 表示）.

(3)、若 $α = 90 °$ ，点 $F$ 在射线 $O B$ 上，若射线 $O F$ 绕点 $O$ 顺时针旋转 $n °$ （ $0 < n < 180 °$ ）， $∠ F O A = 2 ∠ A O D$ ， $O H$ 平分 $∠ E O C$ ，当 $∠ F O H = 120 °$ 时，求 $n$ 的值.

查看试题解析

	月使用费/元	主叫限定时间/ $m i n$	主叫超时费/元/ $m i n$
方式一	58	200	$x$
方式二	88	400	$x + 0.05$