湖北省随州市曾都区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2022-01-05 类型:期末考试
一、单选题
-
1. -4的相反数是( )A、 B、 C、4 D、-42. 下列每组单项式中是同类项的是( )A、2xy与﹣ yx B、3x2y与﹣2xy2 C、 与﹣2xy D、xy与yz3. 下列运用等式的性质变形不一定成立的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则4. 中国“奋斗者”号载人潜水器下潜突破万米,达10909米,创世界纪录.数据10909用科学记数法表示(精确到千位)是( )A、 B、 C、 D、5. 下列语句中正确的是( )A、直线AB和直线BA是两条不同的直线 B、连接两点间的线段叫两点的距离 C、一条射线就是一个周角 D、一个角的余角比这个角的补角小6. 下边几何体的展开图可能是( )
 A、
A、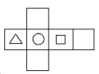 B、
B、 C、
C、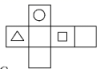 D、
D、 7. 下列说法正确的个数为( ).
7. 下列说法正确的个数为( ).①若a<0, 则; ② 若 , 则a<0;③-a表示负数; ④若a<0;则a3=-a3
A、1个 B、2个 C、3个 D、4个8. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺.则符合题意的方程是( )A、 B、 C、 D、9. 在学习完“解方程”后,老师设计了一个接力游戏,规则是:每人只能看到前一人给出的结果,并进行一步计算再将结果传递给下一人,最后完成解方程,过程如图所示,接力中,自己负责的一步计算正确的是( ) A、甲 B、乙 C、丙 D、丁10. 观察下列图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为 ( )
A、甲 B、乙 C、丙 D、丁10. 观察下列图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为 ( ) A、(2n+1)2 B、(2n-1)2 C、(n+2)2 D、n2
A、(2n+1)2 B、(2n-1)2 C、(n+2)2 D、n2二、填空题
-
11. 如果收入50元记作+50元,那么支出40元记作.12. 方程与方程有相同的解,则a的值等于.13. 有理数a,b,c在数轴上的位置如图所示,化简.
 14. 对于有理数m,n定义运算 , 则.15. 任何一个无限循环小数都可以写成分数的形式.我们以无限循环小数 为例说明如下:设 , 由 可知, , 所以 , 解方程得 , 于是, .请你把 写成分数的形式是.16. 已知点A,B,C都在直线上, , D,E分别为AC,BC中点,若DE的长为6,则AC的长为.
14. 对于有理数m,n定义运算 , 则.15. 任何一个无限循环小数都可以写成分数的形式.我们以无限循环小数 为例说明如下:设 , 由 可知, , 所以 , 解方程得 , 于是, .请你把 写成分数的形式是.16. 已知点A,B,C都在直线上, , D,E分别为AC,BC中点,若DE的长为6,则AC的长为.三、解答题
-
17. 按要求解下列问题:(1)、计算:;(2)、计算:;(3)、解方程:.18. 根据要求求值:(1)、先化简,再求值: , 其中 , ;(2)、已知代数式 的值为 , 求代数式 的值.19. 如图,平面上有四个点A,B,C,D.
 (1)、根据下列语句画图:
(1)、根据下列语句画图:①射线BA;
②直线AD,BC相交于点E;
③延长DC至F(虚线),使CF=BC,连接EF(虚线).
(2)、图中以E为顶点的角中,小于平角的角共有个.20. 小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东跑回到自己家.(1)、以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;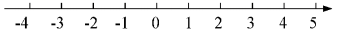 (2)、求小红家与学校之间的距离;(3)、如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?21. 已知点A,B,C在同一直线上, , .
(2)、求小红家与学校之间的距离;(3)、如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?21. 已知点A,B,C在同一直线上, , . (1)、如图1,若点C在点A,B之间,求线段AC的长(2)、如图2,点C在线段AB的延长线上,点D在线段AC上.若 , 求线段CD的长.22. 为了拉动内需,促进国内经济大循环,某超市在“元旦”期间搞促销活动,购物不超过200元不予优惠;购物超过200元不足500元的按全价的90%优惠;超过500元的,其中500元按9折优惠,超过部分按8折优惠.小明两次购物分别用了156元和478元.(1)、若超市不搞促销活动,利用方程求出小明两次购物共值多少钱?(2)、若小明将这两次购物合为一次购买是否更节省?节省多少钱?23. 观察是数学抽象的基础.在数学探究学习中,我们要善于通过观察发现规律,进而解决问题.请你擦亮眼睛,开动脑筋,解答下列问题.(1)、观察下列等式:
(1)、如图1,若点C在点A,B之间,求线段AC的长(2)、如图2,点C在线段AB的延长线上,点D在线段AC上.若 , 求线段CD的长.22. 为了拉动内需,促进国内经济大循环,某超市在“元旦”期间搞促销活动,购物不超过200元不予优惠;购物超过200元不足500元的按全价的90%优惠;超过500元的,其中500元按9折优惠,超过部分按8折优惠.小明两次购物分别用了156元和478元.(1)、若超市不搞促销活动,利用方程求出小明两次购物共值多少钱?(2)、若小明将这两次购物合为一次购买是否更节省?节省多少钱?23. 观察是数学抽象的基础.在数学探究学习中,我们要善于通过观察发现规律,进而解决问题.请你擦亮眼睛,开动脑筋,解答下列问题.(1)、观察下列等式:根据发现的规律,写出第5个等式是 , 第n个等式是;
(2)、根据(1)中发现的规律计算:;(3)、把四张大小相同的长方形卡片(如图1),分别按如图2、图3两种放法互不重叠地放入一个大长方形内,未被长方形卡片覆盖的部分用阴影表示.已知小长方形的长为x,宽为y,请直接写出x与y之间存在的等量关系式;若大长方形的长为a,请直接用含a的整式表示图2中阴影部分的周长与图3中阴影部分的周长的差. 24. 如图1,点O为直线AB上一点,过点O作射线OC,使 , 将一直角三角板( , )的直角顶点放在点O处,一边OM在射线OA上,另一边ON在直线AB的下方.同学们按下列方式玩这块三角板.
24. 如图1,点O为直线AB上一点,过点O作射线OC,使 , 将一直角三角板( , )的直角顶点放在点O处,一边OM在射线OA上,另一边ON在直线AB的下方.同学们按下列方式玩这块三角板. (1)、将图1中的三角板绕点O顺时针旋转一个锐角,使一边OM落在射线OC上,求 的度数;(2)、将图1中的三角板绕点O顺时针旋转一个锐角至图2的位置,使一边OM在 的内部,六个学习小组边玩边测量得到下列数据:
(1)、将图1中的三角板绕点O顺时针旋转一个锐角,使一边OM落在射线OC上,求 的度数;(2)、将图1中的三角板绕点O顺时针旋转一个锐角至图2的位置,使一边OM在 的内部,六个学习小组边玩边测量得到下列数据:组别角
1
2
3
4
5
6
根据表中数据,你猜想 与 之间满足什么等量关系?这一猜想是否正确?并说明理由;
(3)、将图1中的三角板绕点O以每秒 的速度顺时针旋转一周,同时将射线OC绕点O以每秒 的速度顺时针旋转至射线OB,在旋转过程中,是否存在某时刻t,使直线OM恰好平分 ?若存在,求出t的值;若不存在,说明理由.