湖北省荆州市江陵县2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2022-01-05 类型:期末考试
一、单选题
-
1. 5G是第五代移动通信技术,5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是( )A、13×105 B、1.3×105 C、1.3×106 D、1.3×1072. 如果关于x的方程 的解集是 ,那么a的值是( )A、−2 B、−1 C、1 D、23. 如图,一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是( )A、
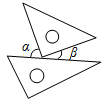 B、
B、 C、
C、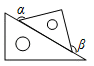 D、
D、 4. 如图,点为线段的中点,点在线段上,如果 , , 那么线段的长是( )
4. 如图,点为线段的中点,点在线段上,如果 , , 那么线段的长是( ) A、4 B、5 C、8 D、105. 下列等式变形正确的是A、如果a=b,那么a+3=b-3 B、如果3a-7=5a,那么3a+5a=7 C、如果3x=-3,那么6x=-6 D、如果2x=3,那么x=6. 有理数a,b在数轴上对应点的位置如图所示,下列说法中正确的是( )
A、4 B、5 C、8 D、105. 下列等式变形正确的是A、如果a=b,那么a+3=b-3 B、如果3a-7=5a,那么3a+5a=7 C、如果3x=-3,那么6x=-6 D、如果2x=3,那么x=6. 有理数a,b在数轴上对应点的位置如图所示,下列说法中正确的是( ) A、a>b B、﹣a>b C、 D、a+b>07. 如图,是正方体的平面展开图,每个面上都标有一个汉字,与“信”字相对的面上的字为( )
A、a>b B、﹣a>b C、 D、a+b>07. 如图,是正方体的平面展开图,每个面上都标有一个汉字,与“信”字相对的面上的字为( ) A、文 B、明 C、法 D、治8. 江陵县青少年活动中心组织实验中学七年级第一批学生前往宜昌参加研学旅行,需要与旅行社联系车辆.如果每辆旅游大巴坐45人,则有28人没有座位,如果每辆坐50人,只有一辆车空12个座位无人坐,其余车辆全部坐满,设有x辆旅游大巴,则可列方程( )A、45x+28=50x﹣12 B、45x﹣28=50x+12 C、45x﹣28=50x﹣12 D、45x+28=50x+129. 对于两个不相等的有理数a,b,我们规定符号max{a,b}表示a,b两数中较大的数,例如max{2,4}=4.按照这个规定,那么方程max{x,-x}=3x-2的解为( )A、 B、1 C、1或 D、 或10. 按如图方式摆放餐桌和椅子:
A、文 B、明 C、法 D、治8. 江陵县青少年活动中心组织实验中学七年级第一批学生前往宜昌参加研学旅行,需要与旅行社联系车辆.如果每辆旅游大巴坐45人,则有28人没有座位,如果每辆坐50人,只有一辆车空12个座位无人坐,其余车辆全部坐满,设有x辆旅游大巴,则可列方程( )A、45x+28=50x﹣12 B、45x﹣28=50x+12 C、45x﹣28=50x﹣12 D、45x+28=50x+129. 对于两个不相等的有理数a,b,我们规定符号max{a,b}表示a,b两数中较大的数,例如max{2,4}=4.按照这个规定,那么方程max{x,-x}=3x-2的解为( )A、 B、1 C、1或 D、 或10. 按如图方式摆放餐桌和椅子:
桌子张数
1
2
3
4
…
n
可坐人数
6
8
10
…
n张餐桌可坐的人数为( )
A、n+5 B、2n+6 C、2n D、2n+4二、填空题
-
11. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为 .
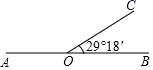 12. 如果一个量的实际值为a,测量值为b,我们把称为绝对误差,称为相对误差.若有一种零件实际长度为5.0cm,测量得4.8cm,则测量所产生的绝对误差是cm,相对误差是cm.13. 若代数式 中不存在含 的一次项,则 的值为 .14. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利(每件商品的利润是商品售价与商品成本价的差)15元,如果设每件商品的成本价为x元,那么每件服装的标价是元,每件服装的实际售价为元,每件服装的利润可表示为 , 则列方程:.15. 如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,正确的作法是连接AC、BD交于点O,则点O就是要找的点,请你用所学过的数学知识解释这一道理.
12. 如果一个量的实际值为a,测量值为b,我们把称为绝对误差,称为相对误差.若有一种零件实际长度为5.0cm,测量得4.8cm,则测量所产生的绝对误差是cm,相对误差是cm.13. 若代数式 中不存在含 的一次项,则 的值为 .14. 一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利(每件商品的利润是商品售价与商品成本价的差)15元,如果设每件商品的成本价为x元,那么每件服装的标价是元,每件服装的实际售价为元,每件服装的利润可表示为 , 则列方程:.15. 如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,正确的作法是连接AC、BD交于点O,则点O就是要找的点,请你用所学过的数学知识解释这一道理. 16. 代数式 中,当 取值分别为 时,对应代数式的值如下表:
16. 代数式 中,当 取值分别为 时,对应代数式的值如下表:···
-1
0
1
2
···
···
-1
1
3
5
···
则 .
三、解答题
-
17. 计算:(1)、-7+(-3)-10-(-16)(2)、-14+(-2)÷(-)-18. 解方程:(1)、;(2)、19. 如图,点是线段外一点.按下列语句画图:

( 1 )画射线;
( 2 )反向延长线段;
( 3 )连接;
( 4 )延长至点 , 使.
20. 依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.解:原方程可变形为 ()
去分母得 ()
去括号得
移项得 ()
()得
系数化为1得
21. 如图1所示,将一副三角尺的直角顶点重合在点O处. (1)、①指出∠AOD和∠BOC的数量关系.
(1)、①指出∠AOD和∠BOC的数量关系.②∠AOC和∠BOD在数量上有何关系?说明理由;
(2)、若将等腰直角三角尺绕点O旋转到如图2的位置.①∠AOD和∠BOC相等吗?说明理由;
②指出∠AOC和∠BOD的数量关系.
22. 为了促进全民健身运动的开展,某市组织了一次足球比赛,下表记录了比赛过程中部分代表队的积分情况.代表队
场次(场)
胜(场)
平(场)
负(场)
积分(分)
6
5
1
0
16
6
6
0
0
18
6
3
2
1
11
6
3
1
2
10
(1)、本次比赛中,胜一场积分;(2)、参加此次比赛的 代表队完成10场比赛后,只输了一场,积分是23分,请你求出 代表队胜出的场数.23. 一般情况下,对于数a和b, , 但是对于某些特殊的数a和b, .我们把这些特殊的数a和b,称为“理想数对”,记作<a,b>.例如当a=1,b=﹣4时,有 , 那么<1,﹣4>就是“理想数对”.(1)、<3,﹣12>,是不是“理想数对”;(填“是”或“不是”)(2)、如果<2,x>是“理想数对”,那么x=;(3)、若<m,n>是“理想数对”,求3[(9n-4m)-8(n- m)]-4m-16的值.24. 阅读思考:小芬在学习过程中,发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示,探索过程如下:如图1所示,线段AB,BC,CD的长度可表示为:AB=3=4﹣1,BC=5=4﹣(﹣1),CD=3=(﹣1)﹣(﹣4),于是他归纳出这样的结论:如果点A表示的数为a,点B表示的数为b,当b>a时,AB=b﹣a(较大数﹣较小数).
(1)、尝试应用:①如图2所示,计算:OE= , EF=;
②把一条数轴在数m处对折,使表示﹣18和2020两数的点恰好互相重合,则m=;
(2)、问题解决:①如图3所示,点P表示数x,点M表示数﹣2,点N表示数2x+14,且MN=4PM,求出点P和点N分别表示的数;
②在上述①的条件下,是否存在点Q,使PQ+QN=3QM?若存在,请直接写出点Q所表示的数;若不存在,请说明理由.
