湖北省黄冈市2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2022-01-05 类型：期末考试

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的倒数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列计算正确的是（　　）

A、 $(- 8) - 8 = 0$ B、 $(- \frac{1}{8}) \times (- 8) = 1$ C、 $- {(- 8)}^{2} = 64$ D、 $| - 8 | = - 8$

查看试题解析
3. 在-1，0，1， $- \frac{1}{3}$ 四个数中，最小的数是（　　）

A、-1 B、0 C、1 D、 $- \frac{1}{3}$

查看试题解析
4. 下列运算中，正确的是（）．

A、 $3 a + 2 b = 5 a b$ B、 $2 a^{3} + 3 a^{2} = 5 a^{5}$ C、 $3 a^{2} b - 3 b a^{2} = 0$ D、 $5 a^{2} - 4 a^{2} = 1$

查看试题解析
5. 已知关于 $x$ 的方程 $3 x + a - 9 = 0$ 的解是 $x = 3$ ，则 $a$ 的值为（）

A、-1 B、0 C、1 D、2

查看试题解析
6. 利用一副三角板上已知度数的角，不能画出的角是（）

A、15° B、100° C、165° D、135°

查看试题解析
7. 如图是正方体的平面展开图，每个面上都标有一个汉字，与“我”字相对的面上的字为（）

A、爱 B、美 C、黄 D、冈

查看试题解析
8. 某种商品的进价为800元，出售标价为1200元，后来由于该商品积压，商店准备打折销售，如果要使得利润率为5%，那么销售时应该打（）

A、6折 B、7折 C、8折 D、9折

查看试题解析

二、填空题

9. 化简： $2 (x + 1) - x =$ .

查看试题解析
10. 一个角的余角是54°38′，则这个角是.

查看试题解析
11. 大量事实证明，环境污染治理刻不容缓，据统计，全球每秒钟约有19.2万吨污水排入江河湖海，把19.2万吨用科学记数法表示为吨.

查看试题解析
12. 若 $- 3 x^{2 m} y^{3}$ 与 $2 x^{4} y^{n}$ 是同类项，那么 $m - n =$ .

查看试题解析
13. 如图，将一刻度尺放在数轴上（数轴上的单位长度是 $1 c m$ ），刻度尺上“ $0 c m$ ”和“ $8 c m$ ”分别对应数轴上的 $- 3$ 和 $x$ ，那么 $x$ 的值为.

查看试题解析
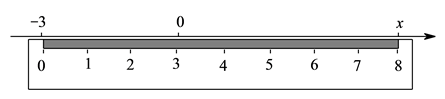14. 如果长方形的周长为 $4 a$ ，它的一边长为 $a - b$ ，则另一边长为.

查看试题解析
15. 在同一平面内，已知 $∠ A O B = 68 °$ ， $∠ B O C = 30 °$ ，则 $∠ A O C =$ .

查看试题解析
16. 已知：如图，线段 $A B = 24 c m$ ， $O A = O P = 2 c m$ ， $∠ P O Q = 60 °$ ，现点 $P$ 绕着点 $O$ 以 $30 ° / s$ 的速度逆时针旋转一周后停止，同时点 $Q$ 沿直线 $B A$ 自点 $B$ 向点 $A$ 运动，若点 $P$ ， $Q$ 两点能相遇，则点 $Q$ 运动的速度为 $c m / s$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $- 1^{2} - (1 - 0.5) \times \frac{1}{2} \times [2 - {(- 2)}^{2}]$ ；

(2)、 $- 19 \frac{18}{19} \times 19$ （简便计算）.

查看试题解析
18. 先化简，再求值 $5 x^{2} - [2 x y - 3 (\frac{1}{3} x y + 2) + 4 x^{2}]$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$

查看试题解析
19. 解下列方程：

(1)、 $3 (2 y + 1) = 2 (1 + y) - (y + 3)$

(2)、 $1 + \frac{x + 5}{6} = x - \frac{x - 1}{3}$

查看试题解析
20. 已知：如图，点 $C$ 、点 $D$ 是线段 $A B$ 上两点，已知 $A C ： C D ： D B = 1 ： 3 ： 5$ ，点 $M$ 、点 $N$ 分别为 $A C$ ， $D B$ 的中点，且 $A B = 18 c m$ ，求线段 $M N$ 的长.

查看试题解析
21. 在某希望实验中学七（8）班的体育课上，体育老师宣布了50米往返“运球”比赛规则，若规定30秒为达标成绩，现对其中一小组学生的成绩记录如下（超过30秒记为正，反之记为负）
人数（人）
2
2
1
1
1
3
成绩（秒）
＋3
－2
0
＋1
＋7
－1

(1)、请计算这一小组学生的平均成绩.

(2)、该小组达标率是多少？

查看试题解析
22. 已知：如图， $B D$ 平分 $∠ A B C$ ， $B E$ 将 $∠ A B C$ 分为2：3两部分， $∠ D B E = 12 °$ ，求 $∠ A B C$ 的度数和 $∠ A B E$ 的补角的度数.

查看试题解析
23. 红旗中学美术课外小组女同学占全组人数的 $\frac{1}{4}$ ，加入6个女同学后，女同学就占全组人数的 $\frac{1}{2}$ ，求美术课外小组原来的人数.

查看试题解析

24. 佳佳平价商场经销的甲、乙两种商品，甲种商品每件售价70元，利润率为40%；乙种商品每件进价40元，售价60元.

(1)、甲种商品每件进价为元，每件乙种商品利润率为.

(2)、若该商场同时购进甲、乙两种商品共30件，恰好总进价为1320元，求购进乙种商品多少件？

(3)、在“元旦”期间，该商场只对甲种商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
少于等于560元	不优惠
超过560元，但不超过700元	按售价打九折
超过700元	其中700元部分八点七折优惠，超过700元的部分打三折优惠

按上述优惠条件，若顾客小贺一次性购买甲种商品实际付款630元，求小贺在该商场购买甲种商品多少件？

查看试题解析

25. 已知：如图，在数轴上点 $A$ 表示数 $a$ ，点 $B$ 表示数 $b$ ， $A B$ 表示 $A$ 点和 $B$ 点之间的距离，且 $a$ ， $b$ 满足 $| a + 2 | + {(b + 3 a)}^{2} = 0$ .

(1)、求 $A$ ， $B$ 两点之间的距离；

(2)、若在数轴上存在一点 $C$ ，且 $A C = 2 B C$ ，求点 $C$ 表示的数；

(3)、一小球甲在数轴上从点 $A$ 处以1个单位/秒的速度向右运动，同时另一小球乙从点 $B$ 处以7个单位/秒的速度向左运动，当甲乙两小球开始运动时，立即在点 $P$ 和点 $B$ 处各放一块挡板，其中点 $P$ 所表示的数为 $- 1$ ，当球在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为 $t$ （秒），问： $t$ 为何值时，甲、乙两小球之间的距离为4.

查看试题解析

人数（人）	2	2	1	1	1	3
成绩（秒）	＋3	－2	0	＋1	＋7	－1