2021-2022学年度第一学期八年级数学第13章《轴对称》13.2画轴对称图形期末复习练习卷（人教版）

试卷更新日期：2022-01-04 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在 $4 \times 4$ 的正方形网格中，有5个小正方形已被涂黑（图中阴影部分），若在其余网格中再涂黑一个小正方形，使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形，则可涂黑的小正方形共有（）个．

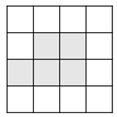A、2 B、3 C、4 D、5

查看试题解析
2. 在平面直角坐标系 $x O y$ 中，对于点 $P (x ， y)$ 和 $Q (x ， y^{'})$ ，给出如下定义：若 $y^{'} = {\begin{array}{l} y (x < 0) \\ - y (x \geq 0) \end{array}$ ，则称点Q为点P的“可控变点”.例如：点 $(1 ， 2)$ 的“可控变点”为点 $(1 ， - 2)$ ，点 $(- 1 ， 3)$ 的“可控变点”为点 $(- 1 ， 3)$ .若点P在函数 $y = - x^{2} + 2 x + 3$ 的图象上，则其“可控变点”Q的纵坐标 $y^{'}$ 关于x的函数图象大致正确的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中剩余的编号1－5的小正方形中任意一个涂黑，则所得图案是一个轴对称图形的概率是（）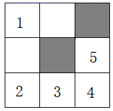

A、1 B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
4. 小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示，现在他将正方形 $A B C D$ 从当前位置开始进行一次平移操作，平移后的正方形的顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有（）

A、3个 B、4个 C、5个 D、无数个

查看试题解析
5. 把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是（）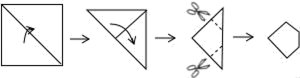

A、六边形 B、八边形 C、十二边形 D、十六边形

查看试题解析
6. 已知：点 $A (m - 1 ， 3)$ 与点 $B (2 ， n - 1)$ 关于 $x$ 轴对称，则 ${(m + n)}^{2021}$ 的值为（）

A、0 B、1 C、-1 D、 $3^{2021}$

查看试题解析
7. 在平面直角坐标系中，点A（2，m）和点B（n ， 3）关于 $x$ 轴对称，则 $\sqrt{{(m + n)}^{2}}$ 的值为（）

A、5 B、﹣5 C、1 D、﹣1

查看试题解析
8. 若点A（﹣3，a）与B（b ， 2）关于x轴对称，则点M（a ， b）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 若点A（a ， 3）与B（2，b）关于x轴对称，则点M（a ， b）的坐标为（）

A、（﹣2，3） B、（2，3） C、（2，﹣3） D、（﹣2，﹣3）

查看试题解析
10. 如图，在平面直角坐标系中，点 $A (3 ， m)$ 在第一象限，若点 $A$ 关于 $x$ 轴的对称点 $B$ 在直线 $y = - x + 1$ 上，则 $m$ 的值为（）

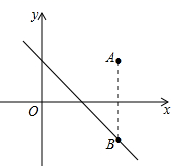A、-1 B、1 C、2 D、3

查看试题解析

二、填空题

11. 如图，在平面直角坐标系 $x O y$ 中， $△ D E F$ 可以看作是 $△ A B C$ 经过若干次的图形变化（轴对称、平移）得到的，写出一种由 $△ A B C$ 得到 $△ D E F$ 的过程：．

查看试题解析
12. 如图，P为∠AOB内一点，M，N分别是射线OA，OB上一点，当△PMN周长最小，且∠OPM＝40°时，则∠AOB＝.

查看试题解析
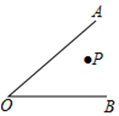13. 如图，点P是∠AOB内任意一点，∠AOB=30°点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是6cm，则OP的长是.

查看试题解析
14. 在平面直角坐标系中，点(1，-7)关于y轴对称的点的坐标是

查看试题解析
15. 点 $(3 + a ， 5)$ 关于 $y$ 轴对称的点的坐标是 $(- 5 ， 4 - b)$ ，则 $b^{a} =$ ．

查看试题解析

三、解答题

16. $△ A B C$ 在平面直角坐标系中的位置如图所示，A、B、C三点在格点上，点B的坐标为 $(1 ， 1)$ ．

（ 1 ）作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

（ 2 ）作出 $△ A_{1} B_{1} C_{1}$ 关于y轴对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $A_{2}$ 的坐标，

查看试题解析
17. 如图，利用关于坐标轴对称的点的坐标的特点，作出 $△$ ABC关于x轴对称的图形.

查看试题解析
18. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点坐标分别是 $A (5 ， 4) ， B (1 ， 1) ， C (5 ， 1)$ ．

⑴请画出 $Δ A B C$ 关于x轴对称的 $Δ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

⑵以O为对称中心，画出 $Δ A B C$ 关于O成中心对称的图形 $Δ A^{'} B^{'} C^{'}$ ；

⑶请用无刻度的直尺画出 $∠ A B C$ 的平分线 $B Q$ （点Q在线段 $A C$ 上）（保留作图辅助线）．

查看试题解析
19. 如图所示，在平面直角坐标系中△ABC的三个顶点坐标分别为A（﹣2，4），B（-4，2），C（﹣3，1）．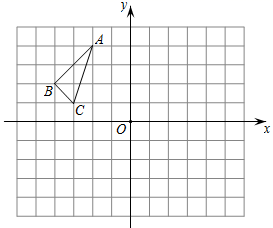

（1）作出△ABC关于x轴对称的△A₁B₁C₁ ，并直接写出A₁点的坐标
（2）作出△ABC关于y轴对称的△A₂B₂C₂ ，并直接写出B₂点的坐标
（3）在（1）（2）的条件下，若点P在x轴上，当A₁P+B₂P的值最小时，直接写出A₁P+B₂P的最小值

查看试题解析
20. 如果点P的坐标为(a，b)，且有(2a+1)²+ $\sqrt{b + 1}$ =0．试求点P关于x轴的对称点P'的坐标．

查看试题解析
21. 如图所示，写出图中点A，B，C，D，E，F，G的坐标，并比较点B与F，C与E，A与G的坐标特征，用文字表述出来．

查看试题解析
22. 如图在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 3 ， 4)$ ， $B (- 4 ， 1)$ ， $C (- 1 ， 1)$

(1)、请在图中画出 $△ A B C$ 关于 $y$ 轴的对称图形 $△ A^{'} B^{'} C^{'}$ ，点 $A$ 、 $B$ 、 $C$ 的对称点分别为 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ ，其中 $A^{'}$ 的坐标为； $B^{'}$ 的坐标为； $C^{'}$ 的坐标为．

(2)、请求出 $△ A^{'} B^{'} C^{'}$ 的面积．

查看试题解析

2021-2022学年度第一学期八年级数学第13章《轴对称》13.2画轴对称图形 期末复习练习卷（人教版）

一、单选题

二、填空题

三、解答题

2021-2022学年度第一学期八年级数学第13章《轴对称》13.2画轴对称图形期末复习练习卷（人教版）