2021-2022学年度第一学期八年级数学第13章《轴对称》13.3等腰三角形 期末复习练习卷（人教版）
试卷更新日期：2022-01-04 类型：复习试卷
一、单选题
-
1. 若一个三角形的三边长为a，b，c，且满足a2-2ab+b2+ac-bc =0，则这个三角形是（ ）A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形2. 若一个等腰三角形的两边m，n满足9m2-n2=-13，3m+n=13，则该等腰三角形的周长为（ ）A、11 B、13 C、16 D、11或163. 如图，在正五边形ABCDE中，连接AD ， 则∠DAE的度数为（ ）
A、46° B、56° C、36° D、26°4. 如图，在 ABC中，AD平分∠BAC ， ，AB=7cm，BD=3cm，则 BDE的周长为（ ）
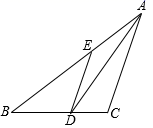A、13cm B、10cm C、4cm D、7cm5. 有一题目：“如图，∠ABC=40°，BD平分∠ABC ， 过点D作DE∥AB交BC于点E ， 若点F在AB上，且满足DF=DE ， 求∠DFB的度数．”小贤的解答：以D为圆心，DE长为半径画圆交AB于点F ， 连接DF ， 则DE=DF ， 由图形的对称性可得∠DFB=∠DEB ． 结合平行线的性质可求得∠DFB=140°．而小军说：“小贤考虑的不周全，∠DFB还应有另一个不同的值”．下列判断正确的是（ ）
A、小军说的对，且∠DFB的另一个值是40° B、小军说的不对，∠DFB只有140°一个值 C、小贤求的结果不对，∠DFB应该是20° D、两人都不对，∠DFB应有3个不同值6. 如图， 是等边三角形，D是线段 上一点（不与点A，C重合），连接 ，点E，F分别在线段 ， 的延长线上，且 ，则 的周长等于（ ）
A、 B、 C、 D、7. 如图所示，已知 是 的角平分线， 于点 ， ， ， ，则 的长为（ ）．
A、3 B、6 C、9 D、128. 如图所示，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则最小值为（ ）
A、2 B、3 C、4 D、69. 如图，在等边 ABC中，AD是它的角平分线，DE⊥AB于E，若AC=8，则BE=（ ）
A、1 B、2 C、3 D、410. 如图，△ABC是边长为2的等边三角形，点P在AB上，过点P作PE⊥AC ， 垂足为E ， 延长BC到点Q ， 使CQ＝PA ， 连接PQ交AC于点D ， 则DE的长为（ ）
A、0.5 B、0.9 C、1 D、1.25二、填空题
-
11. 如图，在等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB，且∠EBD =∠CBD，连接DE、CE，则下列结论； ①∠DAC=∠DBC；②BE⊥AC； ③∠DEB=30°.
④若EC//AD，则S△EBC=1.其中正确的有 ． （只填序号）
12. 如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是 ．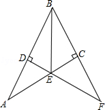
13. 有一个三角形纸片 ， ，点D是 边上一点，沿 方向剪开三角形纸片后，发现所得的两纸片均为等腰三角形，则 的度数可以是 ．
14. 如图， 中，D为AC中点，E为BC上一点，连接DE，且 ，若 ， ，则BC的长度为 ．
15. 如图， 中， ， ，以点C为圆心， 长为半径画弧，交 于点B和点D．若 ，则 的长度是 ．
三、解答题
-
16. 已知：如图，在 中， ，D是BC的中点， ， ，E ， F是垂足， 吗？请说明理由．
17. 如图，点D是△ABC的边BC上一点，AB＝AC＝CD ， ∠BAC＝100°，求∠BAD的度数．
18. 已知在△ABC中，AB＝AC，且线段BD为△ABC的中线，线段BD将△ABC的周长分成12和6两部分，求△ABC三边的长．
19. 如图，已知等边 分别在 上，且 ，连接 交 点．求证：
20. 如图，在△ABC中，∠ACB＝120°，BC＝4，D为AB的中点，DC⊥BC，求AC的长.
解：延长CD到H，使DH＝CD，连接AH，
∵DC⊥BC，∴∠BCD＝90°，（ ▲ ）
∵∠ACB＝120°，∴∠ACD＝30°，
∵D为AB的中点，∴AD＝BD，（ ▲ ）
在△ADH与△BDC中，
∴△ADH≌△BDC（SAS），
∴AH＝ BC＝4，（ ▲ ）
∠H＝∠BCD＝90°，（ ▲ ）
∵∠ACH＝30°，
∴AC＝8.（ ▲ ）
