2021-2022学年度第一学期八年级数学第13章《轴对称》 期末复习练习卷(人教版)
试卷更新日期:2022-01-04 类型:复习试卷
一、单选题
-
1. 下图是设计师石昌鸿设计的《魅力中国》部分城市字体,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ).
2. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ). A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处3. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( )
A、在 AC、BC 两边高线的交点处 B、在 AC、BC 两边垂直平分线的交点处 C、在 AC、BC 两边中线的交点处 D、在∠A、∠B两内角平分线的交点处3. 如图,△ABC中,DE是AB的垂直平分线,△ABC的周长为19cm,△ADC的周长为13cm,则AE的长为( ) A、3cm B、4cm C、6cm D、8cm4. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.
A、3cm B、4cm C、6cm D、8cm4. 如图,在 的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有( )个.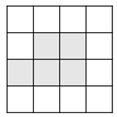 A、2 B、3 C、4 D、55. 若点M(2,a)和点N(a+b,3)关于y轴对称,则a、b的值为( )A、a=3,b=-5 B、a=-3,b=5 C、a=3,b=5 D、a=-3,b=16. 在平面直角坐标系中,点(5,2)关于x轴对称的点的坐标为( )A、(5,-2) B、(-5,2) C、(2,5) D、(2,-5)7. 如图,在正五边形ABCDE中,连接AD , 则∠DAE的度数为( )
A、2 B、3 C、4 D、55. 若点M(2,a)和点N(a+b,3)关于y轴对称,则a、b的值为( )A、a=3,b=-5 B、a=-3,b=5 C、a=3,b=5 D、a=-3,b=16. 在平面直角坐标系中,点(5,2)关于x轴对称的点的坐标为( )A、(5,-2) B、(-5,2) C、(2,5) D、(2,-5)7. 如图,在正五边形ABCDE中,连接AD , 则∠DAE的度数为( ) A、46° B、56° C、36° D、26°8. 如图,在 ABC中,AD平分∠BAC , ,AB=7cm,BD=3cm,则 BDE的周长为( )
A、46° B、56° C、36° D、26°8. 如图,在 ABC中,AD平分∠BAC , ,AB=7cm,BD=3cm,则 BDE的周长为( )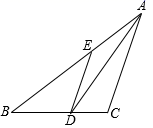 A、13cm B、10cm C、4cm D、7cm9. 如图所示,已知 是 的角平分线, 于点 , , , ,则 的长为( ).
A、13cm B、10cm C、4cm D、7cm9. 如图所示,已知 是 的角平分线, 于点 , , , ,则 的长为( ). A、3 B、6 C、9 D、1210. 如图, ,点 为 内一点,点 分别在 上,当 的周长最小时, 的度数是( )
A、3 B、6 C、9 D、1210. 如图, ,点 为 内一点,点 分别在 上,当 的周长最小时, 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在△ABC 中,AC=BC,∠ACB=90°,点 D 在 BC 上,BD=3,DC=1,点 P 是 AB 上的动点,则 PC+PD 的最小值为
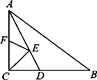
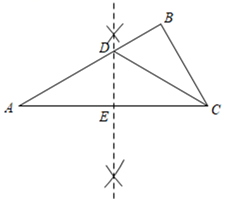
 12. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .
12. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是 .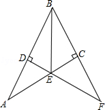 13. 如图,在等边△ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD =∠CBD,连接DE、CE,则下列结论; ①∠DAC=∠DBC;②BE⊥AC; ③∠DEB=30°.
13. 如图,在等边△ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,BE=AB,且∠EBD =∠CBD,连接DE、CE,则下列结论; ①∠DAC=∠DBC;②BE⊥AC; ③∠DEB=30°.④若EC//AD,则S△EBC=1.其中正确的有 . (只填序号)
 14. 如图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点 坐标是 ,则经过第2021次变换后点 的对应点的坐标为 .
14. 如图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点 坐标是 ,则经过第2021次变换后点 的对应点的坐标为 .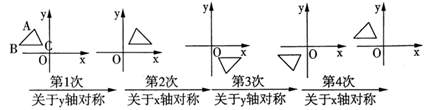 15. 如图,在 中, ,边 的垂直平分线 交 于点D, 平分 ,则 .
15. 如图,在 中, ,边 的垂直平分线 交 于点D, 平分 ,则 .
三、解答题
-
16. 如图,在 ABC中,∠B=90°,∠A=30°.作边AC的垂直平分线交AB于点D , 交AC于点E , 连接CD , 已知BD=4,求∠BCD的度数及AD的长.
 17. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
17. 在平面直角坐标系中的位置如图所示,A、B、C三点在格点上,点B的坐标为 .
( 1 )作出 关于x轴对称的 ,并写出点 的坐标;
( 2 )作出 关于y轴对称的 ,并写出点 的坐标,