2021-2022学年度第一学期八年级数学第11章《三角形》11.2与三角形有关的角 期末复习练习卷(人教版)
试卷更新日期:2022-01-04 类型:复习试卷
一、单选题
-
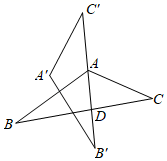
1. 如图 ABC≌ ,边 过点A且平分∠BAC交BC于点D , ∠B=26°, =94°,则 的度数为( )
 A、34° B、40° C、45° D、60°2. 如图,点D在AC上,点B在AE上, ABC≌ DBE . 若∠A:∠C=5:3,则∠DBC的度数为( )
A、34° B、40° C、45° D、60°2. 如图,点D在AC上,点B在AE上, ABC≌ DBE . 若∠A:∠C=5:3,则∠DBC的度数为( ) A、12° B、24° C、20° D、36°3. 如图,在 中, 平分 交 于点D, , ,则 的度数是( )
A、12° B、24° C、20° D、36°3. 如图,在 中, 平分 交 于点D, , ,则 的度数是( )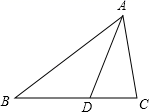 A、 B、 C、 D、4. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、
A、 B、 C、 D、4. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,AD , BE分别是△ABC的中线和角平分线,AB=AC , ∠CAD=20°,则∠ABE的度数为( )
5. 如图,AD , BE分别是△ABC的中线和角平分线,AB=AC , ∠CAD=20°,则∠ABE的度数为( ) A、20° B、35° C、40° D、70°6. 如图,D是△ABC中BC边上一点,AB=AC=BD , 则∠2=24°则∠1=( )
A、20° B、35° C、40° D、70°6. 如图,D是△ABC中BC边上一点,AB=AC=BD , 则∠2=24°则∠1=( )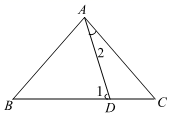 A、44° B、68° C、64° D、54°7. 如图所示,△ABC中,AC=AD=BD , ∠DAC=80°,则∠B的度数为( )
A、44° B、68° C、64° D、54°7. 如图所示,△ABC中,AC=AD=BD , ∠DAC=80°,则∠B的度数为( ) A、40° B、35° C、25° D、20°8. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏东43°方向上,在海岛B的北偏东86°方向上.则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里9. 如图,在 ABC中,∠A=30°,则∠1+∠2的度数为( )
A、40° B、35° C、25° D、20°8. 一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C在海岛A的北偏东43°方向上,在海岛B的北偏东86°方向上.则海岛B到灯塔C的距离是( )A、15海里 B、20海里 C、30海里 D、60海里9. 如图,在 ABC中,∠A=30°,则∠1+∠2的度数为( )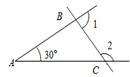 A、210° B、110° C、150° D、100°10. 如图,AB∥DE,∠BCE=53°,∠E=25°,则∠B的度数为( )
A、210° B、110° C、150° D、100°10. 如图,AB∥DE,∠BCE=53°,∠E=25°,则∠B的度数为( ) A、25° B、28° C、30° D、33°
A、25° B、28° C、30° D、33°二、填空题
-
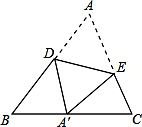
11. 如图,△ABC中,∠A=60°将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′DB=50°,那么∠A′ED的度数为 .
 12. 如图, 中, , ,以点C为圆心, 长为半径画弧,交 于点B和点D.若 ,则 的长度是 .
12. 如图, 中, , ,以点C为圆心, 长为半径画弧,交 于点B和点D.若 ,则 的长度是 . 13. 如图,△ABC是等边三角形,AD⊥BC于点D , AE=AD , 则∠ADE的度数为 .
13. 如图,△ABC是等边三角形,AD⊥BC于点D , AE=AD , 则∠ADE的度数为 . 14. 如图,点D为BC的延长线上一点,图中x的值为 .
14. 如图,点D为BC的延长线上一点,图中x的值为 . 15. 如图, , , ,则 = .
15. 如图, , , ,则 = .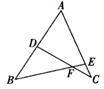
三、解答题
-
16. 已知:如图,在 中, , 于D, 平分 , ,求 的度数.
 17. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数.
17. 如图,点D是△ABC的边BC上一点,AB=AC=CD , ∠BAC=100°,求∠BAD的度数. 18. 如图,在 中, 于点D , 若 ,求 的长.
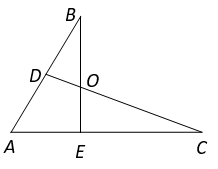
18. 如图,在 中, 于点D , 若 ,求 的长. 19. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O , ∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.
19. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O , ∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.