2021-2022学年度第一学期八年级数学第11章《三角形》期末复习练习卷（人教版）

试卷更新日期：2022-01-04 类型：复习试卷

进入出卷网下载

一、单选题

1. 若一个三角形的三边长为a，b，c，且满足a²-2ab+b²+ac-bc =0，则这个三角形是（）

A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形

查看试题解析
2. 如图，在 $△$ BCD中，CD边上的高是（）

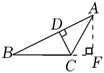A、BD B、AD C、AF D、CD

查看试题解析
3. 如图，一扇窗户打开后，用窗钩 $A B$ 可将其固定，这里所运用的几何原理是（）

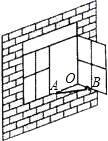A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短

查看试题解析
4. 如图，点D在AC上，点B在AE上， $△$ ABC≌ $△$ DBE ．若∠A：∠C=5：3，则∠DBC的度数为（）

A、12° B、24° C、20° D、36°

查看试题解析
5. 如图，在 $Δ A B C$ 中， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D， $∠ B = 30^{\circ}$ ， $- 3$ ，则 $∠ C$ 的度数是（）

A、 $50^{\circ}$ B、 $60^{\circ}$ C、 $70^{\circ}$ D、 $80^{\circ}$

查看试题解析
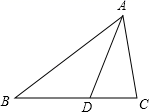6. 如图，在△ABC中，AB＝AC，AD＝DE，∠BAD＝20°，∠EDC＝10°，则∠DAE的度数为（）

A、30° B、40° C、60° D、80°

查看试题解析
7. 如图所示，△ABC中，AC＝AD＝BD ， ∠DAC＝80°，则∠B的度数为（）

A、40° B、35° C、25° D、20°

查看试题解析
8. 从六边形的一个顶点出发最多能画对角线的条数为（）

A、 $5$ 条 B、 $4$ 条 C、3条 D、 $2$ 条

查看试题解析
9. 如图，小明从A点出发，沿直线前进8米后向左转45°，再沿直线前进8米，又向左转45°……照这样走下去，他第一次回到出发点A时，共走路程为（）

A、80米 B、96米 C、64米 D、48米

查看试题解析
10. 一个多边形的每一个外角都为 $36 °$ ，这个多边形是（）

A、四边形 B、六边形 C、八边形 D、十边形

查看试题解析

二、填空题

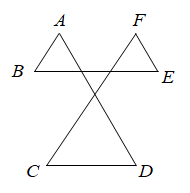
11. 如图，∠A+∠B+∠C+∠D+∠E+∠F＝．

查看试题解析
12. 如图，在△ABC中，点D在BC的延长线上，若∠A=60°，∠B=40°，则∠ACD的度数是．

查看试题解析
13. 如图，△ABC是等边三角形，AD⊥BC于点D ， AE＝AD ，则∠ADE的度数为．

查看试题解析
14. 如图，将 $△$ ABC沿射线BC方向移动，使点B移动到点C ，得到 $△$ DCE ，连接AE ，与DC交于点F ，若 $△$ ABC的面积为6，则 $△$ ACF的面积为．

查看试题解析
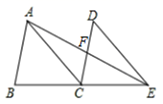15. 等腰△ABC的两边长分别为2和5，则第三边长为.

查看试题解析

三、解答题

16. 一个三角形的三边长分别是xcm、（x+2）cm、（x+5）cm.它的周长不超过37cm.求x的取值范围.

查看试题解析
17. 已知：如图，在 $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A D ⊥ B C$ 于D， $A E$ 平分 $∠ D A C$ ， $∠ B = 62 °$ ，求 $∠ A E C$ 的度数．

查看试题解析
18. 如图，ABCD是四根木条钉成的四边形，为了使它不变形，小明加了根木条AE，小明的做法正确吗？说说你的理由．

查看试题解析
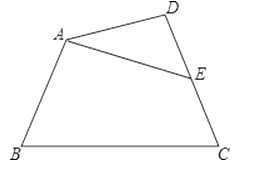19. 如图，在△ABC中，AB=AC，点E是AC上一点，ED⊥BC于点D，DE的延长线交BA的延长线于点F．求证：△AEF是等腰三角形．

查看试题解析
20. 探究与发现：如图①，在Rt△ABC中，∠BAC=90°，AB=AC，点D在底边BC上，AE=AD，连结DE.

(1)、当∠BAD=60°时，求∠CDE的度数；

(2)、当点D在BC （点B、C除外）上运动时，试猜想并探究∠BAD与∠CDE的数量关系；

(3)、深入探究：若∠BAC≠90°，试就图②探究∠BAD与∠CDE的数量关系.

查看试题解析
21. 根据以下提供的 $n$ 边形信息，求 $n$ 边形的内角和．
⑴ $n$ 边形的对角线总条数为 $\frac{n (n - 3)}{2} (n \geq 3)$ .

⑵ $n$ 边形的对角线总条数与边数相等．

查看试题解析
22. 小红把一副直角三角板按如图所示的方式摆放在一起，其中 $∠ B = 90 °$ ， $∠ D = 90 °$ ， $∠ E = 45 °$ ， $∠ A = 30 °$ ，求 $∠ 1 + ∠ 2$ 的度数.

查看试题解析

2021-2022学年度第一学期八年级数学第11章《三角形》 期末复习练习卷（人教版）

一、单选题

二、填空题

三、解答题

2021-2022学年度第一学期八年级数学第11章《三角形》期末复习练习卷（人教版）