2021-2022学年度第一学期八年级数学第12章《全等三角形》12.1全等三角形 期末复习练习卷（人教版）
试卷更新日期：2022-01-04 类型：复习试卷
一、单选题
-
1. 如图 ABC≌ ，边 过点A且平分∠BAC交BC于点D ， ∠B=26°， =94°，则 的度数为（ ）
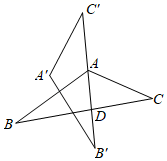A、34° B、40° C、45° D、60°2. 如图， ABC≌ DEC ， B ， C ， D三点在同一直线上，若CE=6，AC=9，则BD的长为（ ）
A、3 B、9 C、12 D、153. 如图，已知 ≌ ， 是 的平分线，已知 ， ，则 的度数是（ ）．
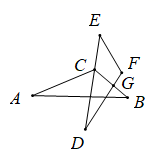A、 B、 C、 D、4. 如图， ，过点A作 ，垂足为点F ， 若 ，则 的度数为（ ）
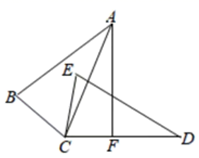A、15° B、25° C、35° D、65°5. 如图，△ABC △DEF，点E，C，F，B在同一条直线上．下列结论正确的是（ ）
A、 B、 C、 D、6. 如图，△ABC≌△BAD，点A和点B，点C和点D是对应点.如果∠D＝70°，∠CAB＝50°，那么∠DAB＝（ ）.
A、20° B、50° C、70° D、60°7. 已知△BCD≌△ABE，下面说法正确的有（ ）个①AB＝BC；②∠BDC＝∠EBA；③∠DBC＝∠BAE；④BD＝EA
A、1 B、2 C、3 D、48. 如图，已知图中的两个三角形全等，则∠α的度数是（ ）
A、72° B、60° C、58° D、50°9. 如图， ABC≌ ADE，若∠BAE＝135°，∠DAC＝55°，那么∠CFE的度数是（ ）
A、80° B、60° C、40° D、20°10. 如图，若 ≌ ， ， ，则CE的长为（ ）
A、1.5 B、2 C、2.5 D、3.5二、填空题
-
11. 如图， ， ， ，则 ．
12. 在平面直角坐标系中，点A(2，0)，B(0，1)，当点C的坐标为 时，△BOC与△ABO全等．13. 如图，在平面直角坐标系中，点A(2，0)，B(0，4)，作△BOC ， 使△BOC与△ABO全等，则点C坐标为 ．
14. 如图，已知 ≌ ，若 ， ，则 的大小为 ．
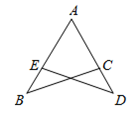15. 如图，△ABC≌△ADE，∠B＝70°，∠C＝26°，∠DAC＝30°，则∠EAC＝.
三、解答题
-
16. 在讲完全等三角形后，教数学的王老师布置了一道数学题：如图所示，已知 ，其中 ， ，则 与 有何位置关系？请说明理由．
17. 如图所示， ADF≌ CBE，且点E，B，D，F在一条直线上，判断AD与BC的位置关系．
