2021-2022学年度第一学期八年级数学第12章《全等三角形》12.2全等三角形的判定 期末复习练习卷（人教版）
试卷更新日期：2022-01-04 类型：复习试卷
一、单选题
-
1. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H（如图）.图中阴影部分的面积记为S，三条线段GB、BC、CH的长度之和记为l，大正六边形在绕点O旋转过程中，下列说法正确的是（ ）
A、S变化，l不变 B、S不变，l变化 C、S变化，l变化 D、S与l均不变2. 如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是（ ）
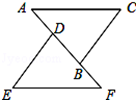A、∠E=∠C B、 AC∥EF C、∠ABC=∠FDE D、 AB=DF3. 如图，在△ABC和△BAD中，已知∠CAB=∠DBA，添加下列条件，还不一定能判定△ABC≌△BAD的是（ ）
A、∠C=∠D B、AC=BD C、BC=AD D、AM=BM4. 如图，点D在AB上．点E在AC上，AB＝AC ． 增加下列一个条件后，仍不能判定△ABE≌△ACD的是（ ）
A、∠AEB＝∠ADC B、∠B＝∠C C、AE＝AD D、BE＝CD5. 如图，在△ABC中，AB=AC，∠ABC、∠ACB的平分线BD，CE相交于O点，且BD交AC于点D，CE交AB于点E.某同学分析图形后得出以下结论：① BCD≌ CBE；② BAD≌ BCD；③ BDA≌ CEA；④ BOE≌ COD；⑤ ACE≌ BCE；上述结论一定正确的是（ ）
A、①②③ B、②③④ C、①③⑤ D、①③④6. 如图，用直尺和圆规作已知角的平分线，要证明 成立的全等三角形的判定依据是（ ）
A、 B、 C、 D、7. 如图，测河两岸A ， B两点的距离时，先在AB的垂线BF上取C ， D两点，使CD＝BC ， 再过点D画出BF的垂线DE ， 当点A ， C ， E在同一直线上时，可证明△EDC≌△ABC ， 从而得到ED＝AB ， 测得ED的长就是A ， B的距离，判定△EDC≌△ABC的依据是：（ ）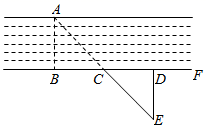
A、ASA B、SSS C、AAS D、SAS8. 下列说法错误的是（ ）A、三边分别相等的两个三角形全等 B、三角分别相等的两个三角形全等 C、两边和它们的夹角分别相等的两个三角形全等 D、斜边和一条直角边分别相等的两个直角三角形全等9. 工人常用角尺平分一个任意角，做法如下：如图， 是一个任意角，在边 、 上分别取 ，移动角尺，使角尺两边相同的刻度分別与点 、 重合，过角尺顶点 作射线 ，由此作法便可得 ，共依据是（ ）
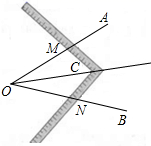A、 B、 C、 D、10. 如图，已知，用直尺和圆规按照以下步骤作图：
①以点O为圆心，任意长为半径画弧，分别交 于点C，D；②画射线 ，以点 为圆心， 长为半径画弧，交 于点 ；③以点 为圆心， 长为半径画弧，与第②步中所画的弧相交于点 ；④过点 画射线 ；根据以上操作，可以判定 ，其判定的依据是（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，AC平分∠DAB ， 要使△ABC≌△ADC ， 需要增加的一个条件是 ．
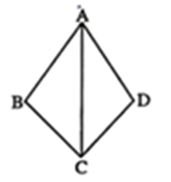12. 如图，四边形ABCD中，AD BC ， ∠A＝90°，AD＝4cm ， BD＝BC＝7cm ， CE⊥BD于点E ， 则DE的长cm ．
13. 如图，在 中， ，点D在边BC上，过点D作 ，垂足为E， ，垂足为D，连接EF，若 ， ，则 的度数为 ．
14. 如图，锐角△ABC的高AD、BE相交于F，若BF=AC，BC=7，CD=2，则AF的长为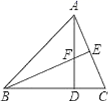
15. 如图，在等边△ABC中，AB=2，D为△ABC内一点，且DA=DB，E为△ABC外一点，BE=AB，且∠EBD =∠CBD，连接DE、CE，则下列结论； ①∠DAC=∠DBC；②BE⊥AC； ③∠DEB=30°.④若EC//AD，则S△EBC=1.其中正确的有 ． （只填序号）
三、解答题
-
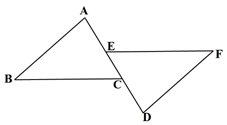
16. 已知：如图，在△ADF和△BCE中，点B，F，E，D依次在一条直线上，若AF∥CE，∠B ∠D ，BF DE，求证：AF CE．
17. 如图， 是等边三角形，若 ， ， ，求 的度数．
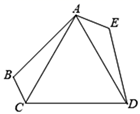18. 已知，如图，AD、BC相交于点O ， AB＝CD ， AD＝CB ． 求证：∠A＝∠C ．
19. 点E、C在线段AD上， AB//DF， AE = DC， CB∥FE求证： △ABC ≌ △DFE
