2021-2022学年度第一学期八年级数学第12章《全等三角形》12.3角的平分线的性质 期末复习练习卷（人教版）
试卷更新日期：2022-01-04 类型：复习试卷
一、单选题
-
1. 如图，在钝角△ABC中，过钝角顶点B作BD⊥BC交AC于点D．用尺规作图法在BC边上找一点P，使得点P到AC的距离等于BP的长，下列作法正确的是（ ）
A、作∠BAC的角平分线与BC的交点 B、作∠BDC的角平分线与BC的交点 C、作线段BC的垂直平分线与BC的交点 D、作线段CD的垂直平分线与BC的交点2. 如图，在 中， ，以顶点 为圆心，适当长为半径画弧，分别交 于点 ，再分别以点 为圆心，大于 的长为半径面弧，两弧交于点 ，作射线 交边 于点 ，若 ，则 的面积是（ ）
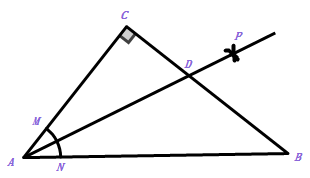A、 B、 C、 D、3. 如图， ， ， 表示三个小城，相互之间有公路相连，现要在 内建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址可以是（ ）．
A、三边中线的交点处 B、三条角平分线的交点处 C、三边上的高交点处 D、三边的中垂线的交点处4. 如图，已知∠AOB求作射线OC，使OC平分∠AOB，那么做法的合理顺序是（ ）.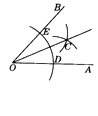
①作射线OC；
②在OA和OB上分别截取OD，OE，使OD=OE；
③分别以D，E为圆心，大于 DE的长为半径作弧，在∠AOB内，两弧交于C．
A、①②③ B、②①③ C、②③① D、③②①5.如图，根据尺规作图的痕迹，判断下列说法不正确的是（ ）
A、AE、BF是△ABC的内角平分线 B、CG也是△ABC的一条内角平分线 C、点O到△ABC三边的距离相等 D、AO=BO=CO6. 已知：如图，∠GBC，∠BAC的平分线相交于点F，BE⊥CF于H，若∠AFB=40°，∠BCF的度数为（ ）
A、40° B、50° C、55° D、60°7. 如图，点P到 、 、 的距离恰好相等，则点P的位置：①在 的平分线上；②在 的平分线上；③在 的平分线上；④恰好是 、 、 三条平分线的交点．上述结论中，正确的个数有（ ）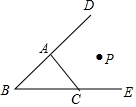
A、 个 B、 个 C、 个 D、 个8. 如图，△ABC的外角∠ACD的平分线CQ与内角∠ABC的平分线BQ交于点Q，若∠BQC=36°，则∠CAQ的度数为（ ）
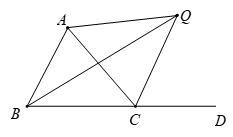A、54° B、62° C、72° D、75°9. 如图，已知点 到 的距离恰好相等，则点 的位置：①在 的平分线上；②在 的平分线上；③在 的平分线上；④恰在 的平分线的交点处 .其中正确的有（ ）
A、4个 B、3个 C、2个 D、1个10. 如图，已知点P到BE，BD，AC的距离恰好相等，则点P的位置：①在∠B的平分线上；②在∠DAC的平分线上；③在∠ECA的平分线上；④恰是∠B，∠DAC，∠ECA三条角平分线的交点，上述结论中，正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图，直线a、b、c分别表示相互交叉的马路，要建一个停车场要求到三条马路的距离相等，那么符合条件的修建点有处.
12. 如图，在Rt△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC、AB于点M、N，再分别以M、N为圆心，任意长为半径画弧，两弧交于点O，作射线AO交BC于点D，若CD＝2，P为AB上一动点，则PD的最小值为.
13. 如图，在Rt 中， ，在边 、 上分别截取 ， ，使 ，分别以D、E为圆心，以大于 的长为半径作弧，两弧在 内交于点M，作射线 交 边于点F.若 ，则点F到 的距离为.
14.如图，在平面直角坐标系中，在x轴、y轴的正半轴上分别截取OA，OB，使OA＝OB；再分别以点A，B为圆心，以大于 AB长为半径作弧，两弧交于点C，若点C的坐标为(m－1，2n)，则m与n的关系为m=（用含n的代数式表示）。
15. 如图， 是矩形 的对角线，在 和 上分别截取 ，使 ；分别以 为圆心，以大于 的长为半径作弧，两弧在 内交于点 ，作射线 交 于点 ，若 ，则点 到 的距离为.
三、解答题
-
16. 已知：如图，Rt△ABC中，∠ACB=90°
(1)、用直尺和圆规作∠ABC的平分线，交AC于点O；(2)、在（1）的条件下，若BC=3，AC=4，求点O到AB的距离。17. 近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P，张、李两村坐落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请你通过作图确定P点的位置．
18.为了美化环境，某小区要在如图所示的三角形空地上作一个半圆形花坛并使之满足以下要求：
①圆心在边BC上；
②该半圆面积最大．请你帮忙设计这一花坛．
19. 如图，点P为 和 的平分线的交点．求证：点P在 的平分线上．
