广东省东莞市2021-2022学年八年级上学期第三次月考数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 在下列以线段a、b、c的长为边,能构成三角形的是( )A、a=3,b=4,c=8 B、a=5,b=6,c=11 C、a=6,b=8,c=9 D、a=7.b=17,c=252. 下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是( )A、
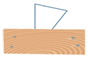 B、
B、 C、
C、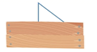 D、
D、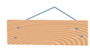 3. 自新冠肺炎疫情发生以来,莆田市积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
3. 自新冠肺炎疫情发生以来,莆田市积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、 有症状早就医
B、
有症状早就医
B、 打喷捂口鼻
C、
打喷捂口鼻
C、 防控疫情我们在一起
D、
防控疫情我们在一起
D、 勤洗手勤通风
4. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
勤洗手勤通风
4. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( ) A、2 B、9 C、10 D、125. 下列各式计算正确的是( )A、a2+a2=a4 B、2a2×2a2=2a4 C、(a﹣b)2=a2﹣b2 D、(4ab+1)(4ab﹣1)=16a2b2﹣16. 如图,ΔABC中,三条中线AD,BE,CF相交于点O,若ΔABC的面积是10,则△OCD的面积是( )
A、2 B、9 C、10 D、125. 下列各式计算正确的是( )A、a2+a2=a4 B、2a2×2a2=2a4 C、(a﹣b)2=a2﹣b2 D、(4ab+1)(4ab﹣1)=16a2b2﹣16. 如图,ΔABC中,三条中线AD,BE,CF相交于点O,若ΔABC的面积是10,则△OCD的面积是( ) A、2 B、1.5 C、 D、57. 若x2+mx+n分解因式的结果是(x﹣2)(x+1),则m+n的值为( )A、﹣3 B、3 C、1 D、﹣18. 满足下列条件的三角形中,不是直角三角形的是( )A、∠A﹣∠B=∠C B、∠A=9°,∠B=81° C、∠A=2∠B=3∠C D、∠A:∠B:∠C=3:4:79. 如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,交AB于点E,已知∠CAD:∠DAB=1:2,则∠B=( )
A、2 B、1.5 C、 D、57. 若x2+mx+n分解因式的结果是(x﹣2)(x+1),则m+n的值为( )A、﹣3 B、3 C、1 D、﹣18. 满足下列条件的三角形中,不是直角三角形的是( )A、∠A﹣∠B=∠C B、∠A=9°,∠B=81° C、∠A=2∠B=3∠C D、∠A:∠B:∠C=3:4:79. 如图,在△ABC中,∠C=90°,AB的垂直平分线交BC于点D,交AB于点E,已知∠CAD:∠DAB=1:2,则∠B=( )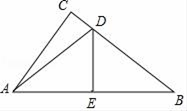 A、34° B、36° C、60° D、72°10. 如图,把纸片的沿折叠,点A落在四边形外,则、与的关系是( ).
A、34° B、36° C、60° D、72°10. 如图,把纸片的沿折叠,点A落在四边形外,则、与的关系是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 若x2+8x+m是完全平方式则m的值为 .13. 直角三角形的两边长是6和8,则这个三角形的面积是.14. 已知正多边形的一个外角等于 , 则这个正多边形的内角和的度数为.15. 若点A(a,4)和点B(﹣1,b+5)关于y轴对称,则点a+b= .16. 如图,BD是△ABC的角平分线,DE⊥AB于点E.△ABC的面积为20,AB=12,BC=8,则DE的长为 .
 17. 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为.
17. 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上;△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形.若OA1=1,则△A2015B2015A2016的边长为.
三、解答题
-
18. 已知一个多边形的内角和与外角和的差为1080°,求这个多边形的边数.
19. 如图所示,点E,F在AC上,AB∥CD,AB=CD,AE=CF,求证△ABF≌△CDE. 20. 已知:CD平分∠ACB,BF是△ABC的高,若∠A=70°∠ABC=60°求∠BMC的度数.
20. 已知:CD平分∠ACB,BF是△ABC的高,若∠A=70°∠ABC=60°求∠BMC的度数. 21. 先化简,再求值: , 其中 .22. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
21. 先化简,再求值: , 其中 .22. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. (1)、在图中画出与△ABC关于直线l成轴对称的△A1B1C1;(2)、△A1B1C1的面积为 ;(3)、线段CC1被直线l .23. 已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,
(1)、在图中画出与△ABC关于直线l成轴对称的△A1B1C1;(2)、△A1B1C1的面积为 ;(3)、线段CC1被直线l .23. 已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF,
求证:(1)AE∥FB,
(1)、DE=CF.24. 如图a是一个长为2m、宽为2n的长方形,沿图中实线用剪刀均分成四块小长方形,然后按图b的形状拼成一个大正方形.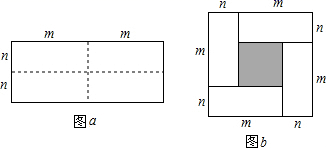 (1)、如图b中的小正方形的边长等于_;(2)、如图a中四个长方形的面积和为_ , 如图b中四个小长方形的面积和还可以表示为_;(3)、由(2)写出代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系:_;(4)、根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,求(2x﹣2y)2的值.25. 如图,在Rt△ABC中,∠ACB=90°,CD为AB上的高,AF为∠BAC的角平分线,AF交CD于点E,交BC于点F.
(1)、如图b中的小正方形的边长等于_;(2)、如图a中四个长方形的面积和为_ , 如图b中四个小长方形的面积和还可以表示为_;(3)、由(2)写出代数式:(m+n)2 , (m﹣n)2 , mn之间的等量关系:_;(4)、根据(3)中的等量关系,解决如下问题:若x+y=8,xy=7,求(2x﹣2y)2的值.25. 如图,在Rt△ABC中,∠ACB=90°,CD为AB上的高,AF为∠BAC的角平分线,AF交CD于点E,交BC于点F. (1)、如图1,①∠ACD ▲ ∠B(选填“<,=,>”中的一个)
(1)、如图1,①∠ACD ▲ ∠B(选填“<,=,>”中的一个)②如图1,求证:CE=CF;
(2)、如图1,作EG∥AB交BC于点G,若AD=a,△EFG为等腰三角形,求AC(含a的代数式表示);(3)、如图2,过BC上一点M,作MN⊥AB于点N,使得MN=ED,探索BM与CF的数量关系.