河北省邢台市信都区2021-2022学年九年级上学期12月月考数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 如果两个相似三角形对应边的比为1:4,那么它们的周长比是( )A、1:2 B、1:4 C、1:8 D、1:162. 若一元二次方程(x﹣2)2=9可转化为两个一元一次方程,一个一元一次方程是x﹣2=3,则另一个一元一次方程是( )A、x﹣2=3 B、x﹣2=﹣3 C、x+2=3 D、x+2=﹣33. 已知⊙O的半径等于8cm,圆心O到直线l的距离为9cm,则直线l与⊙O的公共点的个数为( )A、0 B、1 C、2 D、3个或3个以上4. 如图所示,点M是⊙O上的任意一点,下列结论:

①以M为端点的弦只有一条;②以M为端点的直径只有一条;③以M为端点的弧只有一条.则( )
A、①、②不符合题意,③符合题意 B、②、③不符合题意,①符合题意 C、①、③不符合题意,②符合题意 D、①、②、③不符合题意5. 如图所示的正方形网格中,A,B,C三点均在格点上,那么ABC的外接圆圆心是( ) A、点E B、点F C、点G D、点H6. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
A、点E B、点F C、点G D、点H6. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( ) A、4 B、﹣4 C、8 D、﹣87. 如图,是⊙O的直径,点C、D在⊙O上,且在异侧,连接、、 . 若 , 则的大小是( )
A、4 B、﹣4 C、8 D、﹣87. 如图,是⊙O的直径,点C、D在⊙O上,且在异侧,连接、、 . 若 , 则的大小是( ) A、15° B、25° C、35° D、50°8. 如图,以O为位似中心且与ABC位似的图形编号是( )
A、15° B、25° C、35° D、50°8. 如图,以O为位似中心且与ABC位似的图形编号是( )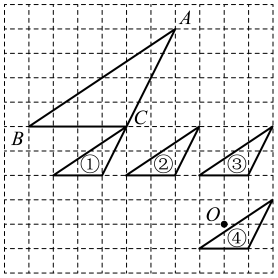 A、① B、② C、③ D、④9. 已知一组数据的方差s2=[(6﹣7)2+(10﹣7)2+(a﹣7)2+(b﹣7)2+(8﹣7)2](a,b为常数),则a+b的值为( )A、5 B、7 C、10 D、1110. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( )
A、① B、② C、③ D、④9. 已知一组数据的方差s2=[(6﹣7)2+(10﹣7)2+(a﹣7)2+(b﹣7)2+(8﹣7)2](a,b为常数),则a+b的值为( )A、5 B、7 C、10 D、1110. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( ) A、8cm B、7cm C、6cm D、5cm11. 如图所示是三个反比例函数 , , 在轴右边的图象,由此观察得到、、的大小关系是( )
A、8cm B、7cm C、6cm D、5cm11. 如图所示是三个反比例函数 , , 在轴右边的图象,由此观察得到、、的大小关系是( )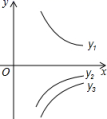 A、 B、 C、 D、12. 如图,有三个小海岛A、B、C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A( )
A、 B、 C、 D、12. 如图,有三个小海岛A、B、C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A( ) A、北偏东20°方向 B、北偏东30°方向 C、北偏东40°方向 D、北偏西30°方向13. 某品牌服装平均每天可以售出20件,每件盈利40元.受新冠肺炎疫情影响,商场决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价4元,平均每天就可以多售出8件,如果需要盈利1200元,那么每件降价多少元?设每件降价x元,下列方程正确的是( )A、(40﹣x)(20+×8)=1200 B、(40﹣x)(20+8x)=1200 C、(40﹣x)(×8)=1200 D、40×(20+×8)=120014. 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A、北偏东20°方向 B、北偏东30°方向 C、北偏东40°方向 D、北偏西30°方向13. 某品牌服装平均每天可以售出20件,每件盈利40元.受新冠肺炎疫情影响,商场决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:每件服装每降价4元,平均每天就可以多售出8件,如果需要盈利1200元,那么每件降价多少元?设每件降价x元,下列方程正确的是( )A、(40﹣x)(20+×8)=1200 B、(40﹣x)(20+8x)=1200 C、(40﹣x)(×8)=1200 D、40×(20+×8)=120014. 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )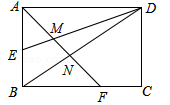 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 若一组数据1,2,3,x,1,3,2有唯一的众数2,则这组数据的平均数是 , 中位数是 .16. 在数学课上,老师请同学思考如下问题:
已知:在ABC中,∠A=90°.

求作:⊙P,使得点P在边AC上,且⊙P与AB,BC都相切.
嘉淇的主要作法如下:
如图,

⑴作∠ABC的平分线BF,与AC交于点P;
⑵以点P为圆心,AP长为半径作⊙P.所以⊙P即为所求.
老师说:“嘉淇的作法符合题意.”请回答:⊙P与BC相切的依据是①;② .
17. 如图,在ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE⊥AB于点E,AE=6,cosA= . (1)、CD=;(2)、tan∠DBC= .
(1)、CD=;(2)、tan∠DBC= .三、解答题
-
18. 如图,已知ABC中,∠C=90°,AC=3,BC=4,以点C为圆心作⊙C,半径为r.
 (1)、当r取什么值时,点A在⊙C外?(2)、当r取什么值时,点A在⊙C内,点B在⊙C外.19. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若△AOB绕点O逆时针旋转90º后,得到△A1OB1(A和A1是对应点)
(1)、当r取什么值时,点A在⊙C外?(2)、当r取什么值时,点A在⊙C内,点B在⊙C外.19. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若△AOB绕点O逆时针旋转90º后,得到△A1OB1(A和A1是对应点) (1)、作出△A1OB1;(2)、求旋转过程中边OB扫过的面积(结果保留π);20. 已知反比例函数 , 其中 , 且 , .(1)、若随的增大而增大,则的取值范围是;(2)、若该函数的最大值与最小值的差是 , 求的值.21. 疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:
(1)、作出△A1OB1;(2)、求旋转过程中边OB扫过的面积(结果保留π);20. 已知反比例函数 , 其中 , 且 , .(1)、若随的增大而增大,则的取值范围是;(2)、若该函数的最大值与最小值的差是 , 求的值.21. 疫情期间,某药店出售一批进价为2元的口罩,在市场营销中发现此口罩的日销售单价x(元)与日销售量y(只)之间有如下关系:日销售单价x(元)
3
4
5
6
日销售量y(只)
2000
1500
1200
1000
(1)、猜测并确定y与x之间的函数关系式;(2)、设经营此口罩的销售利润为W元,求出W与x之间的函数关系式?(3)、若物价局规定此口罩的售价最高不能超过10元/只,请你求出当日销售单价x定为多少时,才能获得最大日销售利润?最大利润是多少元?22. 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE. (1)、求证:D是BC的中点;(2)、若DE=4, AD=2,求⊙O的半径.23. 在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线经过点 , 记双曲线与两坐标轴之间的部分为(不含双曲线与坐标轴).
(1)、求证:D是BC的中点;(2)、若DE=4, AD=2,求⊙O的半径.23. 在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线经过点 , 记双曲线与两坐标轴之间的部分为(不含双曲线与坐标轴). (1)、求的值;(2)、求内整点的个数;(3)、设点在直线上,过点分别作平行于轴轴的直线,交双曲线于点 , 记线段、双曲线所围成的区域为 , 若内部(不包括边界)不超过8个整点,求的取值范围.24. 已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切.
(1)、求的值;(2)、求内整点的个数;(3)、设点在直线上,过点分别作平行于轴轴的直线,交双曲线于点 , 记线段、双曲线所围成的区域为 , 若内部(不包括边界)不超过8个整点,求的取值范围.24. 已知在矩形ABCD中,AB=4,AD=3,⊙C与对角线BD相切. (1)、如图1,求⊙C的半径;(2)、如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC= , 求∠CPA的度数和弧PQ的长;(3)、如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤时,请直接写出∠PCE度数的取值范围.
(1)、如图1,求⊙C的半径;(2)、如图2,点P是⊙C上一个动点,连接AP,AC,AP交⊙C于点Q,若sin∠PAC= , 求∠CPA的度数和弧PQ的长;(3)、如图,对角线AC与⊙C交于点E,点P是⊙C上一个动点,设点P到直线AC的距离为d,当0<d≤时,请直接写出∠PCE度数的取值范围.