广东省揭阳市惠来县西片区联考2021-2022学年九年级上学期12月月考数学试题
试卷更新日期:2022-01-04 类型:月考试卷
一、单选题
-
1. 下列方程中,一定是关于x的一元二次方程的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、(a-2)2=a2-43. 下列命题中,为真命题的是( )
⑴对角线互相平分的四边形是平行四边形(2)对角线互相垂直的四边形是菱形(3)对角线相等的平行四边形是菱形(4)有一个角是直角的平行四边形是矩形
A、(1)(2) B、(1)(4) C、(2)(4) D、(3)(4)4. 为了庆祝中国共产党成立100周年,某校举办了党史知识竞赛活动,在获得一等奖的学生中,有3名女学生,1名男学生,则从这4名学生中随机抽取2名学生,恰好抽到2名女学生的概率为( )A、 B、 C、 D、5. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、6. 如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm , OA′=20cm , 则五边形ABCDE的周长与五边形A′B′C′D′E′的周长比是( )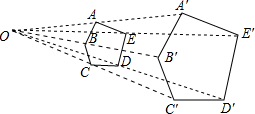 A、1:2 B、2:1 C、1:3 D、3:17. 如图,在中,点、、分别在 , , 边上, , , 则下列比例式中错误的是( )
A、1:2 B、2:1 C、1:3 D、3:17. 如图,在中,点、、分别在 , , 边上, , , 则下列比例式中错误的是( )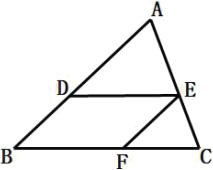 A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则整数a的最大值是( )A、4 B、5 C、6 D、79. 如图,在菱形中,P是对角线上一动点,过点P作于点E.于点F.若菱形的周长为24,面积为24,则的值为( )
A、 B、 C、 D、8. 若关于x的一元二次方程 有实数根,则整数a的最大值是( )A、4 B、5 C、6 D、79. 如图,在菱形中,P是对角线上一动点,过点P作于点E.于点F.若菱形的周长为24,面积为24,则的值为( )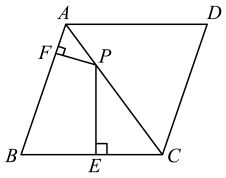 A、4 B、 C、6 D、10. 如图,在正方形中,顶点在坐标轴上,且 , 以为边构造菱形 . 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2020次旋转结束时,点的坐标为( )
A、4 B、 C、6 D、10. 如图,在正方形中,顶点在坐标轴上,且 , 以为边构造菱形 . 将菱形与正方形组成的图形绕点逆时针旋转,每次旋转 , 则第2020次旋转结束时,点的坐标为( )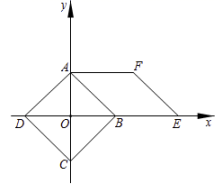 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
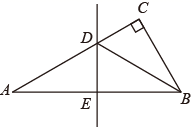
11. 若0是一元二次方程的一个根,则m的值为 .12. 在菱形ABCD中,对角线AC=30,BD=60,则菱形ABCD的面积为 .13. 如图,在中, , , 线段AB的垂直平分线分别交AC、AB于点D、E,连结BD.若 , 则AD的长为 .
 14. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
14. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°. 15. 已知点 是线段 的黄金分割点( ),如果 ,那么线段 .16. 观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.
15. 已知点 是线段 的黄金分割点( ),如果 ,那么线段 .16. 观察右边立体图得到它的主视图、左视图和俯视图,请写在对应图的下边.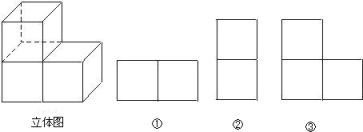
① , ② , ③ .
17. 如图是一张矩形纸片,点E在AB边上,把 沿直线CE对折,使点B落在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上,AE=2,则DF= , BE= .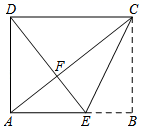
三、解答题
-
18. 解下列方程:(1)、x2﹣6x+3=0;(2)、3x(x﹣2)=2(x﹣2).19. 已知一元二次方程的一个根为2(1)、求q关于p的关系式;(2)、求证:方程有两个不等的实数根.20. 如图,中, .
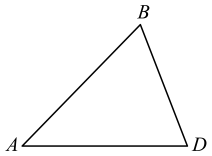 (1)、作点A关于的对称点C;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图中,连接 , , 连接 , 交于点O.求证:四边形是菱形.21. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查,调查结果分为:A(实时关注)、B(关注较多)、C(关注较少)、D(不关注)四类,现将调查结果绘制成如图所示的统计图.
(1)、作点A关于的对称点C;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)所作的图中,连接 , , 连接 , 交于点O.求证:四边形是菱形.21. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查,调查结果分为:A(实时关注)、B(关注较多)、C(关注较少)、D(不关注)四类,现将调查结果绘制成如图所示的统计图.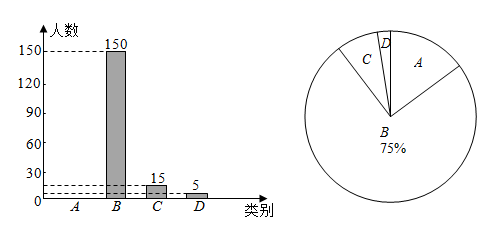
请根据图中信息,解答下列问题:
(1)、求C类职工所对应扇形的圆心角度数,并补全条形统计图;(2)、若D类职工中有3名女士和2名男士,现从中任意抽取2人进行随访,请用树状图或列表法求出恰好抽到一名女士和一名男士的概率.22. 如图,在中,于点E,交于点F,且 .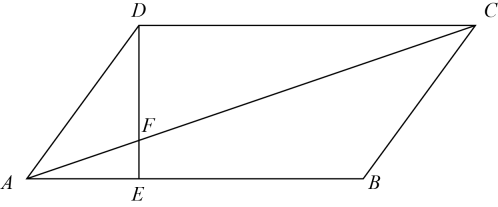 (1)、求证:;(2)、求与的面积比.23. 如图,在矩形 中,E是 的中点, ,垂足为F.
(1)、求证:;(2)、求与的面积比.23. 如图,在矩形 中,E是 的中点, ,垂足为F.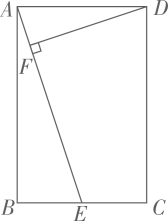 (1)、求证: ;(2)、若 , ,求 的长.24. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、当销售单价为90元时,每月的销售量为 件.(2)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(3)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?25. 如图,在菱形ABCD中, , , 点E为边AB上一个动点,延长BA到点F,使 , 且CF、DE相交于点G
(1)、求证: ;(2)、若 , ,求 的长.24. 某超市销售一种商品,每件成本为50元,销售人员经调查发现,销售单价为100元时,每月的销售量为50件,而销售单价每降低2元,则每月可多售出10件,且要求销售单价不得低于成本.(1)、当销售单价为90元时,每月的销售量为 件.(2)、求该商品每月的销售量y(件)与销售单价x(元)之间的函数关系式;(不需要求自变量取值范围)(3)、若使该商品每月的销售利润为4000元,并使顾客获得更多的实惠,销售单价应定为多少元?25. 如图,在菱形ABCD中, , , 点E为边AB上一个动点,延长BA到点F,使 , 且CF、DE相交于点G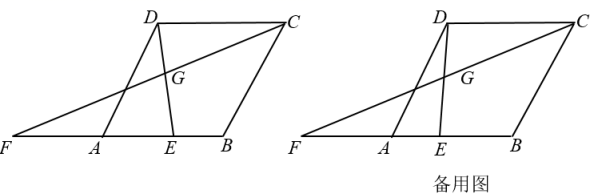 (1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.
(1)、当点E运动到AB中点时,证明:四边形DFEC是平行四边形;(2)、当时,求AE的长;(3)、当点E从点A开始向右运动到点B时,求点G运动路径的长度.